
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Класифікація алгоритмів на основі функції трудомісткостіСодержание книги
Поиск на нашем сайте Подальше дослідження алгоритмів на основі функції трудомісткості пов'язане з визначенням тих факторів, які впливають на значення функції трудомісткості. До цих факторів можна віднести кількість елементів множини D, значення цих елементів і порядок їх розміщення. На основі такого дослідження можна побудувати класифікацію алгоритмів по ступені впливу цих факторів на функцію трудомісткості. Виділимо в функції fA(D) кількісну складову (залежну від n) і параметричну складову (залежну від значень і порядку слідування елементів в D), позначивши їх через fn(n) та gp(D)відповідно: fА(D) = fА(fn(n),gp(D)). Для більшості алгоритмів ця залежність може бути представлена як композиція функцій fn(n) та gp(D)або в мультиплікативній формі: fА(D) = fn(n) · або в адитивній формі: fА(D) = fn(n) + Введемо наступні позначення:
В залежності від впливу різних характеристик множини вхідних даних на функцію трудомісткості алгоритму, може бути запропонована наступна класифікація алгоритмів: 1. КласN (Numerical)– клас кількісно залежних по трудомісткості алгоритмів. Це алгоритми, функція трудомісткості яких, залежить тільки від розмірності вхідних даних g+(n)=0, g*(n)=1 => fА(D) = fn(n) Прикладами алгоритмів з кількісно-залежною функцією трудомісткості можуть слугувати алгоритми для стандартних операцій роботи з масивами і матрицями, наприклад, множення матриць, множення матриці на вектор і т.д. Аналіз таких алгоритмів, як правило, не викликає труднощів. Зауважимо, що для алгоритмів класу N справедливе співвідношення
2. КласPR (Рarametritic) – клас параметрично залежних по трудомісткості алгоритмів. Це алгоритми, трудомісткість яких визначається не розмірністю входу (як правило, для цього класу розмірність входу фіксована), а конкретними значеннями всіх або деяких елементів із вхідної множини D: fn(n)=const = с => fА(D) = c · Прикладами алгоритмів з параметрично-залежною трудомісткістю є алгоритми обчислення стандартних функцій із заданою точністю шляхом обчислення відповідних степеневих рядів. Такі алгоритми, маючи на вході два числових значення - аргумент функції і точність, задають залежну тільки від їх значень кількість операцій. Наприклад: - обчислення значення xk методом послідовного множення, fА(D) = fА(x,k); - обчислення значення експоненти із заданою точністю ε:
3. КласNPR – клас кількісно-параметрично залежних по трудомісткості алгоритмів. Це досить широкий клас алгоритмів, тому що в більшості практичних випадків функція трудомісткості залежить як від кількості даних на вході, так і від їхніх значень. У цьому випадку fn(n)≠const, g*(n)≠1 => fА(D) = fn(n) · В якості приклада можна навести ряд алгоритмів чисельних методів, в яких параметрично-залежний зовнішній цикл по точності містить у собі кількісно-залежний фрагмент по розмірності, що породжує мультиплікативну форму для fА(D).
В залежності від ступеня впливу кількісної і параметричної складових на головний порядок функції трудомісткості виділяють наступні підкласи у класі кількісно-параметричних алгоритмів: 3.1. ПідкласNPRL (Low)– підклас алгоритмів, трудомісткость яких слабо залежить від параметричної складової. g+(n)=O(fn (n)) <=> g*(n)= Ө(1). До цього підкласу відноситься, наприклад, алгоритм пошуку максимального елемета в масиві, тому що кількість переприсвоювань максимуму в найгіршому випадку (коли масив відсортований по зростанню) має рівний порядок з оцінкою зовнішнього циклу для перебору n елементів. 3.2. ПідкласNPRE (Equivalent ) – підклас алгоритмів, у трудомісткості яких складова g*(n) має порядок росту, не перевищуючий fn (n): g*(n)= Ө(fn (n)) <=> g+(n)=Ө( Таким чином, для алгоритмів цього підкласу вплив на головний порядок функції трудомісткості параметричного компоненту має той самій порядок (в мультиплікативній формі), що й кількісного компоненту. Для алгоритмів, що відносяться до цього підкласу, можна говорити про квадратично-кількісну функцію трудомісткості. В цей підклас входить, наприклад, алгоритм сортування масиву методом бульбашки, для якого кількість перестановок елементів у найгіршому випадку (коли масив відсортований по спаданню) визначає порядок g+(n)= Ө(n2), fn (n)= Ө(n). 3.3. ПідкласNPRH (High)– підклас алгоритмів, у трудомісткості яких складова g*(n) має асимптотичний порядок росту вищий, ніж fn (n): g*(n)= Ω(fn (n)) Для алгоритмів цього підкласу саме параметричний компонент визначає головний порядок функції трудомісткості. Можна говорити, що ці алгоритми є кількісно-сильно-параметричними по функції трудомісткості алгоритмами. У цей підклас входять, наприклад, алгоритми точного розв'язання NP-повних задач. Для алгоритмів цього підкласу характерна, як правило, мультиплікативна форма функції трудомісткості, що особливо яскраво виражена в алгоритмах більшості ітераційних обчислювальних методів. У них зовнішній цикл по точності породжує параметричну складову, а трудомісткість тіла циклу має кількісну оцінку.
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 953; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.007 с.) |

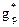 (D),
(D), (D).
(D).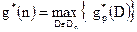
 ,
, 
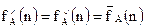
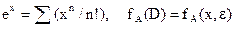
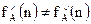
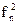 (n)).
(n)).


