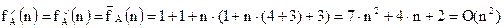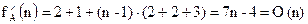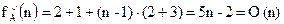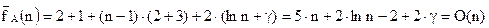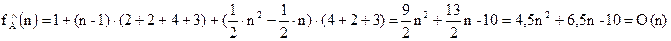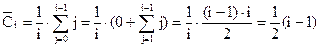Приклади аналізу трудомісткості алгоритмів

Як приклади застосування методики для аналізу алгоритмів по функції трудомісткості розглянемо декілька алгоритмів, що відносяться до класу N і різним підкласам класу NPR.

 

Приклад 1 (алгоритм знаходження суми елементів квадратної матриці)

 

int suma (int a[][],const int n){
int i, j, s = 0;	1 операція
for (i=0; i<n; i++) {	1 операція. Всього n проходів циклу
for (j=0; j<n; j++) {	1 операція. Всього n проходів циклу
s = s + a[i][j];	4 операції на кожний прохід циклу
}	3 операції на кожний прохід циклу
}	3 операції на кожний прохід циклу
return s;
}

 

Цей алгоритм виконує однакову кількість операцій при фіксованому значенні n. Таким чином, він є кількісно-залежним і належить до класу N. Функція трудомісткості обчислюється для цього алгоритму за формулою:

 

Приклад 2 (алгоритм пошуку максимального елемента масиву)

 

int maximum(int a[],const int n){
int max = a[0];	2 операції
for(int i=1; i<n; i++) {	1 операція. Всього (n-1) проходів циклу
if (a[i] > max)	2 операції на кожний прохід циклу
max = a[i];	2 операції на кожний прохід циклу
}	3 операції на кожний прохід циклу
return max;
}

Стосовно операцій порівняння цей алгоритм є кількісно-залежним, оскільки завжди треба перевиряти всі n елементів. Але кількість операцій присвоювання залежить від місця, де саме розташований найбільший елемент в послідовності, тобто стосовно операцій перестановок цей алгоритм є кількісно-параметрично залежним. Отже, в загальному даний алгоритм є кількісно-параметрично залежним і належить до класу NPRS. Тому при фіксованому розмірі вхідних даних необхідно проводити окремий аналіз для найгіршого, найкращого та середнього випадків.

1) Найгірший випадок – найбільша кількість операцій присвоювання (max=a[i]) буде тоді, коли елементи масиву посортовані по зростанню. Трудомісткість алгоритму в такому випадку рівна:

2) Найкращий випадок – мінімальна кількість переприсвоювань максимального числа буде в тому випадку, коли максимальний елемент розташований на першому місці в масиві. Трудомісткість алгоритму в такому випадку рівна:

3) Середній випадок. Алгоритм пошуку максимуму послідовно перебирає елементи масиву, порівнюючи поточний елемент масиву з поточним значенням максимуму. На черговому кроці, коли проглядається і-ий елемент масиву, переприсвоювання максимуму відбудеться тоді, коли в підмасиві з перших і елементів максимальним елементом буде останній.

Очевидно, що у випадку рівномірного розподілу a[i], ймовірність того, що максимальний з і елементів розташований в певній (останній) позиції дорівнює 1/і. Тоді в масиві з n елементів загальна кількість операцій присвоювання визначається як:

 

де γ≈ 0. 577216 ... (ця сума називається n -им гармонійним числом и позначається H_n; константа γ називається константою Ейлера).

Таким чином, значення середньої кількості операцій присвоювання в алгоритмі пошуку максимума в масиві з n елементів визначається як:

 

Приклад 3 (алгоритм сортування масиву)

void sort (int a[],const int n){
int i, j, x;
for (i=1; i<n; i++) {	1 операція. Всього (n-1) проходів циклу for
x = a[i];	2 операції на кожний прохід циклу for
j = i-1;	2 операції на кожний прохід циклу for
while ((j>=0) && (a[j]>x)) {	4 операції на кожний прохід циклу for
a[j+1] = a[j];	4 операції на кожний прохід циклу while
j-=1;	2 операції на кожний прохід циклу while
a[j+1] = x;	3 операції на кожний прохід циклу while
}
}	3 операції на кожний прохід циклу for
}

Алгоритм відноситься до класу NPRS, тому що кількість порівнянь і переміщень визначається для фіксованого набору значень елементів порядком їхнього розташування у вхідному масиві.

Тому при фіксованому розмірі вхідних даних необхідно проводити окремий аналіз для найгіршого, найкращого та середнього випадків.

Найгірший випадок – найбільша кількість операцій переміщень буде тоді, коли елементи масиву посортовані по спаданню. Спочатку порахуємо максимальну кількість переміщень для всіх елементів. Перший елемент масиву a[0] здійснить 0 переміщень, наступний елемент a[1] здійснить 1 переміщення і т.д., останній елемент масиву a[n-1] здійснить (n-1) переміщення. Отже:

 

Трудомісткість алгоритму в такому випадку рівна:

2) Найкращий випадок – мінімальна кількість переміщень буде тоді, коли елементи масиву посортовані по зростанню і непотрібно виконувати жодного переміщення. Трудомісткість алгоритму в такому випадку рівна:

3) Середній випадок. Для аналізу трудомісткості в середньому спочатку визначимо середню кількість порівнянь для і-го елемента:

 

Підсумуємо для всіх (n-1) елементів, які треба вставити:

 

 

Використовуючи методику аналізу алгоритмічних конструкцій, остаточно маємо:

 

ПОРЯДОК ВИКОНАННЯ РОБОТИ

1. При підготовці до лабораторної роботи, необхідно засвоїти теоретичний матеріал по темі і підготуватись до контрольного опитування по розумінню питань даної тематики.

2. Згідно з індивідуальним завданням розробити алгоритм розв’язання задачі.

3. Підготувати програмну реалізацію розробленого алгоритму. Засобами вбудованого тексто-вого редактора інтегрованого середовища набрати текст підготовленої програми. Відкомпілювати, налагодити та виконати програму.

4. Протестувати програму згідно зі складеною системою тестів і, при потребі, відкоректувати текст програми. Проаналізувати отримані результати.

5. Написати контрольне опитування по темі.

6. Оформити звіт по роботі.

Без підготовкі до лабораторної роботи (програмної реалізації розробленого алгоритму) студент до роботи не допускається.