
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналіз складності алгоритмівСодержание книги Поиск на нашем сайте
Методичні вказівки До лабораторної роботи № 3
з дисципліни " AЛГОРИТМИ ТА МЕТОДИ ОБЧИСЛЕНЬ"
для студентів напряму 6.050102 “Комп’ютерна інженерія”
Львів – 2010 Методичні вказівки до комплексу лабораторних робіт з дисципліни "AЛГОРИТМИ ТА МЕТОДИ ОБЧИСЛЕНЬ" для підготовки студентів напряму 6.050102 “Комп’ютерна інженерія” / Укл. Т.А.Лисак – Львів: Видавництво НУ “Львівська політехніка”, 2010 – 18 с.
Укладач: Матвейчук Т.А., ст. викладач каф.ЕОМ
Відповідальний за випуск: Мельник А.О., д-р техн. наук, проф.
Рецензенти: Мороз І.В., ст. викладач каф.ЕОМ
Юрчак І.Ю., доцент кафедри САПР, к.т.н.
МЕТА РОБОТИ Оволодіти методикою аналізу складності основних алгоритмічних конструкцій. Навчитись обчислювати функцію трудомісткості. Ознайомитись з класифікацією алгоритмів на основі функції трудомісткості. Опанувати методику аналізу розроблених алгоритмів на предмет їх складності. ТЕОРЕТИЧНІ ВІДОМОСТІ Складність алгоритмів Для оцінки алгоритмів існує багато критеріїв. Найбільшу увагу приділяють порядку росту, необхідного для розв'язання задачі часу та розміру пам'яті при збільшені вхідних даних. З кожною конкретною задачею зв'язане число, яке називається розміром задачі і яке виражає міру кількості вхідних даних. Наприклад, розміром задачі множення матриць може бути найбільший розмір матриць-співмножників. Розміром задачі про графи може бути число ребер даного графа. Час, затрачений на обчислення при виконанні алгоритму, являє собою суму часів окремих виконаних операторів. Програму, написану на мові високого рівня, можна перетворити прямим (хоча і не простим) шляхом в програму на машинному коді заданої ЕОМ. Це в принципі дає метод оцінки часу виконання вказаної програми, але такий підхід орієнтований на конкретну ЕОМ і не дає загальної залежності часу обчислення від розмірів задачі. В області аналізу та побудови алгоритмів прийнято виражати час виконання, як і будь-яку іншу міру ефективності, з точністю до мультиплікативної константи. Це, зазвичай, робиться шляхом підрахунку лише певних ключових операцій, виконаних алгоритмом (що легко здійснити, аналізуючи версію цього алгоритму, записану на мові високого рівня). Такий підхід абсолютно правомірний при визначені нижніх оцінок часу виконання, оскільки невраховані операції можуть лише збільшити їх; однак при роботі з верхніми оцінками ми повинні впевнитись у тому, що вклад вибраних ключових операцій в сумі відрізняється не більше, ніж в константу раз від вкладу всіх операцій, виконаних алгоритмом. Час, який витрачається алгоритмом, як функція розміру задачі, називається часовою складністю цього алгоритму. T(n). Асимптотику поведінки цієї функції при збільшенні розміру задачі називають асимптотичною часовою складністю, а для її позначення використовують нотацію Ландау (велике O). Аналогічно, можна виділити просторову складність та асимптотичну просторову складність. Саме асимптотична складність визначає розмір задач, які алгоритм здатен обробити. Наприклад, якщо алгоритм обробляє вхідні дані розміром n за час cn², де c - деяка стала, то кажуть, що часова складність такого алгоритму O(n²). Просторова та часова складності як функції від розмірів задачі є дві фундаментальні оцінки ефективності при аналізі алгоритмів. Аналіз середньої асимптотичної часової складності можна поділити на два типи: аналітичний та статистичний. Аналітичний метод дає точніші результати, але складний у використанні на практиці. Натомість статистичний метод дозволяє швидше здійснювати аналіз складних задач. В основах аналізу алгоритмів до одного класу відносять всі функції, чий порядок росту однаковий з точністю до постійного множника. Ці класи, їх назви, а також деякі пояснення та приклади, наведені в таблиці 1 у відповідності до зростання їхнього порядку росту. Функції, які зростають повільніше, наведені першими. В таблиці прийнято, що n
Таблиця 1. Основні асимптотичні класи ефективності
2.2. Функція трудомісткості і система позначень Знання асимптотичних оцінок складностей різних алгоритмів розв'язання певного завдання дає можливість порівнювати ці алгоритми з точки зору їхньої ефективності. Однак асимптотичні оцінки вказують лише на порядок функцій, і результати порівняння будуть справедливі тільки при дуже великих розмірах вхідних даних. Для порівняння ефективності алгоритмів при реальних розмірах входних даних і прогнозування часу виконання їхніх програмних реалізацій необхідне знання про точну кількість операцій досліджуваних алгоритмів, що характеризується функцією трудомісткості. Під трудомісткістю алгоритму для даної конкретної проблеми, що задається множиною D, розуміють кількість "елементарних" операцій, що задаються алгоритмом у прийнятій моделі обчислень. Відповідну функцію позначають як fА(D). Значенням функції трудомісткості є ціле додатнє число. Введемо спеціальні позначення, пов'язані із граничними значеннями функції трудомісткості даного алгоритму при фіксованій довжині входу. Нехай DA — множина допустимих конкретних проблем даної задачі, що розв'язується алгоритмом А (наприклад, множина комбінацій розміщення елементів вхідного масиву для алгоритму сортування).
У загальному випадку існує підмножина множини DA, що містить всі конкретні проблеми, що мають розмірність n. Позначимо її через Dn:
Позначимо потужність множини Dn через МDn =|Dn|. Тоді алгоритм А, маючи на вході різні множини Введемо наступні позначення:
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1372; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.40.195 (0.009 с.) |


 ∞, с - константа.
∞, с - константа. — конкретна проблема (вхід алгоритму А), що представляє собою впорядковану множину елементів (слів) d:
— конкретна проблема (вхід алгоритму А), що представляє собою впорядковану множину елементів (слів) d: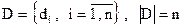

 , буде, можливо, задавати в деякому випадку найбільшу, а в деякому випадку найменшу кількість операцій.
, буде, можливо, задавати в деякому випадку найбільшу, а в деякому випадку найменшу кількість операцій. – найгірший випадок – найбільша кількість операцій, які необхідно виконати алгоритмом А для вирішення конкретної проблеми розмірністю n:
– найгірший випадок – найбільша кількість операцій, які необхідно виконати алгоритмом А для вирішення конкретної проблеми розмірністю n:

 – найкращий випадок – найменша кількість операцій, які необхідно виконати алгоритмом А для вирішення конкретної проблеми розмірністю n:
– найкращий випадок – найменша кількість операцій, які необхідно виконати алгоритмом А для вирішення конкретної проблеми розмірністю n:
 – середній випадок – середня кількість операцій, які необхідно виконати алгоритмом А для вирішення конкретної проблеми розмірністю n:
– середній випадок – середня кількість операцій, які необхідно виконати алгоритмом А для вирішення конкретної проблеми розмірністю n: .
.


