
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обґрунтування алгоритму ДейкстриСодержание книги Поиск на нашем сайте
Мітка вершини v (l(v)!= Нехай вершина v одержала свою постійну мітку на k-й ітерації, тобто після k-го виконання кроку 4 алгоритму Дейкстри. У разі k = 1 твердження очевидне. Припустимо, що воно справджується для вершин, які отримали свої постійні на ітераціях із номерами 2,3,…,k-1. Позначимо як Р0 шлях від a до v, побудований з алгоритмом Дейкстри за k ітерацій, а як Р* - найкоротший шлях від a до v. Довжину шляху Р позначатимемо як w(P). За умовою w(Р0) = l(v). Нехай М і Т = V\M – множини вершин відповідно з постійними та тимчасовими мітками перед початком k-ї ітерації. Розглянемо ситуацію перед початком k–ї ітерації. Можливі два випадки.
Випадок 1. Деякі вершини шляху Р* належать множині Т. Нехай Випадок 2. Усі вершини шляху Р* містяться в множині М. Нехай v‘ та v* - вершини, які безпосередньо передують вершині v відповідно в шляхах Р* та Р0. Позначимо як P ’ частину шляху Р* від початкової вершини a до вершини v ‘. За припущенням індукції w(P ‘) >= l(v ’), то w(P*) = w(P ’) + w(v ‘, v) >= l(v ‘) + e(v ’, v) = w(Р0). Припустимо тепер, що v ’!= v*. Позаяк v одержує постійну мітку l(v) з v*, а не з v ‘, то w(P*) = l(v ’) + w(v ‘, v) >= l(v*, v) = w(Р0). Отже, і у випадку 2 справджується нерівність w(P*) >= w(Р0), тобто Р0 – найкоротший шлях від a до v. Якщо граф подано матрицею суміжності, складність алгоритму Дейкстри становить О(n2). Коли кількість дуг m значно менша ніж n2, то найкраще подавати орієнтований граф списками суміжності. Тоді алгоритм можна реалізувати зі складністю О(m log n), що в цьому разі істотно менше, ніж О(n2).
Алгоритм Дейкстри дає змогу обчислити довжину найкоротшого шляху від початкової вершини a до заданої вершини z. Для знаходження самого шляху потрібно лише нагромаджувати вектор вершин, з яких найкоротший шлях безпосередньо потрапляє в дану вершину. Для цього з кожною вершиною v графа G, окрім вершини a, зв’язують іще одну мітку – О(v). Крок 2 модифікують так. Для кожної вершини v є Г(х)\М якщо l(v) >l(x) + w(x, u), то l(v):= l(x) + w(x, u) та О(v):= x, а ні, то не змінювати l(v) та О(v). Коли мітка l(v) стане постійною найкоротший <a,v> - шлях буде потрапляти у вершину v безпосередньо з вершини х. Із постійних міток l(v) та О(v) утворюють вектори l і O.
Приклад 3.33. Знайдемо довжину найкоротшого шляху від початкової вершини а до вершини z у графі на рис. 3.37, а. Послідовність дій зображено на рис. 3.37, б-е, мітки записано в дужках біля вершин. Вершини, які включено в множину М, обведено кружечками; мітки таких вершин оголошують постійними. У процесі роботи алгоритму будують два вектори: вектор l постійних міток (довжини найкоротших шляхів від вершини а до даної вершини) і вектор
Рис. 3.37 Алгоритм Дейкстри Таблиця 3.4
Ми розглянули задачу відшукання в графі найкоротшого шляху від якоїсь виділеної (початкової) вершини до будь-якої іншої. Розглянемо задачу пошуку в графі найкоротшого шляху між кожною парою вершин. Звичайно, цю загальнішу задачу можна розв'язати багатократним застосуванням алгоритму Дейкстри з послідовним вибором кожної вершини графа як початкової. Проте є й прямий спосіб розв'язання цієї задачі за допомогою алгоритму Флойда. У ньому довжини дуг можуть бути від'ємними, проте не може бути циклів із від'ємною довжиною. Нехай G= (V, E) — орієнтований граф. Нагадаємо, що внутрішні вершини шляху a, x1, x2, xm-u в графі G — х1, х2, …, хm-1. Наприклад, внутрішні вершини шляху а, с, d, а, f, b — с, d, а, f. Пронумеруємо вершини графа цілими числами від 1 до n. Позначимо як
В алгоритмі Флойда як початкову беруть матрицю W(0). Спочатку за нею обчислюють матрицю W(1) потім — W(2), і процес повторюють доти, доки за матрицею W(n-1) не буде обчислено матрицю W(n) Розглянемо ідею, на якій ґрунтується алгоритмі Флойда. Припустимо, що відомі.
1. Найкоротший шлях із вершини і у вершину k, у якому як внутрішні використано лише перші (k-1) вершин. 2. Найкоротший шлях із вершини k у вершину j, у якому як внутрішні використано лише перші (k - 1) вершин. 3. Найкоротший шлях із вершини і у вершину j, у якому як внутрішні використано лише перші (k - 1) вершин. Оскільки за припущенням граф G не містить циклів із від'ємною довжиною, то один із двох шляхів — шлях із п. 3 чи об'єднання шляхів із пп. 1 і 2 — найкоротший шлях із вершини і у вершину j, у якому як внутрішні використано лише перші (k - 1) вершин. Отже,
Зі співвідношення (3.1) видно, що для обчислення елементів матриці w
Алгоритм Флойда Наведемо кроки алгоритму. Крок 1. Присвоювання початкових значень. Пронумерувати вершини графа Gцілими числами від 1 до n. Побудувати матрицю W(0)= W, задавши кожний її (i,j)-елемент такий, що дорівнює вазі дуги, котра з'єднує вершину і з вершиною j. Якщо в графі G ці вершини не з'єднано дугою, то виконати Крок 2. Цикл. Для k, що послідовно набуває значення 1, 2, …, п, визначити за елементами матриці W(k-1) елементи матриці W(k) використовуючи рекурентне співвідношення (3.1). Після закінчення цієї процедури (і,j) - елемент матриці W(n) дорівнює довжині найкоротшого шляху з вершини і у вершину j. Якщо під час роботи алгоритму для якихось k й і виявиться, що
Якщо заздалегідь відомо, що в графі Є немає циклів із від'ємною довжиною, то обсяг обчислень можна дещо зменшити. У цьому разі для всіх і та всіх k має бути Приклад 3.34. Знайти найкоротші шляхи між усіма парами вершин орієнтованого графа на рис. 3.38.
Рис. 3.38 Граф до прикладу 3.34
Нижче наведено результати виконання кожної з чотирьох
W(0)= W=
W(1)=
W(2)=
W(3)=
W(4)=
Матриця W(4) дає довжини найкоротших шляхів між усіма парами вершин графа на рис. 3.38. Зокрема, Очевидно, що як алгоритм Дейкстри, так і алгоритм Флойда можна застосовувати без жодних змін і до неорієнтованих графів. Для цього достатньо кожне ребро {и, V}, що має вагу
Обхід графів Існує багато алгоритмів на графах, які ґрунтуються на систематичному переборі їх вершин або обході вершин, під час якого кожна вершина одержує унікальний порядковий номер. Алгоритми обходу вершин графа називають методами пошуку [23]. 3.9.1. Пошук углиб у простому зв'язному графі Опишемо метод пошуку в простому зв'язному графі, який являє собою одну з основних методик проектування алгоритмів, пов'язаних із графами. Цей метод називають пошуком углиб, або DFS - методом (від англ. depth first search).
Нехай G = (V, Е) — простий зв'язний граф, усі вершини якого позначено попарно різними символами. У процесі пошуку вглиб вершинам графа G надають номери (DFS - номери) та певним способом позначають ребра. У ході роботи алгоритму використовують структуру даних для збереження множин, яку називають стеком (англ. stack — стіг). Зі стеку можна вилучити тільки той елемент, котрий було додано до нього останнім: стек працює за принципом «останнім прийшов — першим вийшов» (last in, first out — скорочено LIFO). Інакше кажучи, додавання й вилучення елементів у стеку відбувається з одного кінця, який називають верхівкою стеку. DFS - номер вершини х позначають DFS(x).
Таблиця 3.5
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 740; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.12.100 (0.012 с.) |

 ) дорівнює довжині <a,v> - шляху, побудованого за алгоритмом до певного моменту. Тому достатньо довести, що постійна мітка l(v) кожної вершини v дорівнює довжині найкоротшого <a,v> - шляху. Отже, доведемо що значення l(v) – постійної мітки вершини v- дорівнює довжині найкоротшого шляху від початкової вершини a до вершини v. Для доведення цього застосуємо математичну індукцію.
) дорівнює довжині <a,v> - шляху, побудованого за алгоритмом до певного моменту. Тому достатньо довести, що постійна мітка l(v) кожної вершини v дорівнює довжині найкоротшого <a,v> - шляху. Отже, доведемо що значення l(v) – постійної мітки вершини v- дорівнює довжині найкоротшого шляху від початкової вершини a до вершини v. Для доведення цього застосуємо математичну індукцію.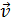 - перша (починаючи від a) з тих вершин шляху Р*, які належать множині Т, а вершина v ’ безпосередньо передує
- перша (починаючи від a) з тих вершин шляху Р*, які належать множині Т, а вершина v ’ безпосередньо передує  маємо, що v ‘ є М. Позначимо як Р1* частину шляху Р* від a до
маємо, що v ‘ є М. Позначимо як Р1* частину шляху Р* від a до 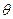 вершин, з яких у дану вершину безпосередньо потрапляє найкоротший шлях. У табл. 3.4 в першому рядку містяться довільно впорядковані вершини графа, у другому — відповідні постійні мітки (компоненти вектора l), а в третьому — компоненти вектора
вершин, з яких у дану вершину безпосередньо потрапляє найкоротший шлях. У табл. 3.4 в першому рядку містяться довільно впорядковані вершини графа, у другому — відповідні постійні мітки (компоненти вектора l), а в третьому — компоненти вектора 



 довжину найкоротшого шляху з вершини і у вершину j, у якому як внутрішні можуть бути лише перші k вершин графа G. Якщо між вершинами і тa j не існує жодного такого шляху, то умовно вважатимемо, що
довжину найкоротшого шляху з вершини і у вершину j, у якому як внутрішні можуть бути лише перші k вершин графа G. Якщо між вершинами і тa j не існує жодного такого шляху, то умовно вважатимемо, що  . Зі сказаного випливає, що
. Зі сказаного випливає, що  — це вага дуги (ij), а якщо такої дуги немає, то
— це вага дуги (ij), а якщо такої дуги немає, то  дорівнює довжині найкоротшого шляху з вершини і у вершину j. Позначимо як W
дорівнює довжині найкоротшого шляху з вершини і у вершину j. Позначимо як W  nxn матрицю, (і, j)-й елемент якої дорівнює
nxn матрицю, (і, j)-й елемент якої дорівнює  (3.1)
(3.1) . Тепер ми можемо формально описати алгоритм Флойда для знаходження в графі найкоротших шляхів між усіма парами вершин.
. Тепер ми можемо формально описати алгоритм Флойда для знаходження в графі найкоротших шляхів між усіма парами вершин.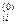 := 0.
:= 0. < 0, то в графі G існує цикл із від'ємною довжиною, який містить вершину і. Тоді роботу алгоритму потрібно припинити.
< 0, то в графі G існує цикл із від'ємною довжиною, який містить вершину і. Тоді роботу алгоритму потрібно припинити.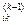 =
= 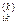 ,
,  =
= 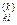 які випливають із того, що коли немає циклів із від'ємною довжиною, вершина k не може бути внутрішньою в будь-яких найкоротших шляхах, котpі починаються чи закінчуються в самій вершині k. Отже, обчислюючи матрицю немає потреби переобчислювати елементи k-го рядка й k-го стовпця матриці W(k-1). Отже, у матриці W(k) за формулою (3.1) потрібно обчислювати лише k2 – З × п + 2 елементи. Очевидно, що складність алгоритму Флойда становить 0(п3). Щоб після закінчення його роботи можна було швидко знайти найкоротший шлях між будь-якою парою вершин, на k-й ітерації разом із матрицею W(k) побудуємо матрицю
які випливають із того, що коли немає циклів із від'ємною довжиною, вершина k не може бути внутрішньою в будь-яких найкоротших шляхах, котpі починаються чи закінчуються в самій вершині k. Отже, обчислюючи матрицю немає потреби переобчислювати елементи k-го рядка й k-го стовпця матриці W(k-1). Отже, у матриці W(k) за формулою (3.1) потрібно обчислювати лише k2 – З × п + 2 елементи. Очевидно, що складність алгоритму Флойда становить 0(п3). Щоб після закінчення його роботи можна було швидко знайти найкоротший шлях між будь-якою парою вершин, на k-й ітерації разом із матрицею W(k) побудуємо матрицю  (k) =[
(k) =[ 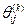 ]. Спочатку беремо
]. Спочатку беремо  :=і для всіх і,j= 1, …, п,
:=і для всіх і,j= 1, …, п,  ;
;  := 0. Далі, на к-й ітерації візьмемо
:= 0. Далі, на к-й ітерації візьмемо  , якщо
, якщо  =
=  і
і  , якщо
, якщо  =
=  . Отже,
. Отже,  ] відіграє ту саму роль, що й вектор
] відіграє ту саму роль, що й вектор 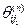 , j3=
, j3=  , ….
, ….







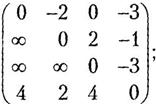


 , тобто довжина найкоротшого шляху від вершини 2 до вершини 1 дорівнює 3. Для знаходження самого шляху скористаємося матрицею
, тобто довжина найкоротшого шляху від вершини 2 до вершини 1 дорівнює 3. Для знаходження самого шляху скористаємося матрицею  = 4,
= 4,  = 3,
= 3,  = 2. Отже, найкоротший шлях із вершини 2 у вершину 1 проходить через вершини 2, 3, 4, 1.
= 2. Отже, найкоротший шлях із вершини 2 у вершину 1 проходить через вершини 2, 3, 4, 1.



