Деякі спеціальні класи простих графів

Розглянемо деякі спеціальні класи простих графів, часто використовувані як приклади й широко застосовувані [15].

Повний граф з п вершинами (позначають як К_п) — це граф, у якому будь-яку пару вершин з'єднано точно одним ребром.

Приклад 3.9. На рис. 3.9 зображено графи К_п для п = 1, 2, 3, 4, 5.

 

Рис. 3.9 Повні графи

Граф називають порожнім, якщо Е = 0, тобто такий граф не має ребер. Порожній граф з п вершинами можна розбити на дві підмножини У₄ і У₂, що не перетинаються (V_X U V₂=V, V_x U У₂ = 0), так, що кожне ребро з'єднує вершину з V, і вершину з V₂. Дводольний граф називають повним, якщо кожну вершину з У₄ з'єднано ребром із кожною вершиною з V₂. Повний дводольний граф позначають як К_т, де т= \У_Х\, п= |У₂|. Граф К_х називають зіркою.

Граф К_т×п має п + т вершин та п×т ребер.

Приклад 3.10. На рис. 3.10 наведено повні дводольні графи K_i5, K₃₂ та К₃₃.

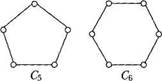
Рис. 3.10 Дводольні графи

Циклом С_п, п > 3, називають граф із множиною вершин і множиною ребер Е={{o_t, v₂}, {v₂, v^},..., {v_n^, v_n), {v_n, v_x}}.

Приклад 3.11. На рис. 3.11 зображено цикли C₃, C₄, C₅ i C₆.

 

Рис. 3.11 Цикли

Колесом W_n називається граф, який можна одержати з циклу С_п додаванням іще однієї вершини, з'єднаної з усіма и вершинами в С_п новими ребрами.

Приклад 3.12. На рис. 3.12 зображено колеса W₃, W₄, W₅, W₆.

Рис. 3.12. Колеса

Простий граф, вершини якого зображають yсі 2 бітові рядки довжиною п, називають п - вимірним кубом і позначають Q_п. Дві вершини в Q _п з'єднано ребром тоді и лише тоді, коли бітові рядки, які їx подають, відрізняються точно в одному біті.

Граф Q_n+1 можна отримати з двох графsв Q з'єднавши ребрами їxнi однаково позначені вершини. Після цього до бітових рядків у вершинах одного з графів Q_n зліва дописують 0, другого — 1.

Приклад 3.13. На рис. 3.13 зображено графи Q₁, Q₂ та Qз

Рис. 3.13 N-вимірні куби

Способи подання графів

Найзрозуміліший і корисний для людини cпоcі6 подання (зображення) графів — це рисунок на площині у вигляді точок і ліній, які з'єднують ці точки. Проте цей cпoсі6 подання абсолютно непридатний, якщо потрібно розв'язувати на комп'ютері задачі з графами.

Розглянемо декілька інших способів подання графів для двох найважливіших графів: простого й орієнтованого (рис. 3.15).

Рис. 3.15 Простий та орієнтований граф

 

Матрицю, кожний елемент якої дорівнює 0 чи 1, називають булевою.

3.3.1. Матриця інцидентності

Нехай G=(V,E) — простий граф із множиною вершин V={v₁ , v ₂,..., v_n } і множиною ребер Е - {е₁, е₂,..., е_т).

Матрицею інцидентності графа G, яка відповідає заданій нумерації вершин і ребер, називають булеву п×т матрицю М з елементами m_ij (і = 1,..., п; j = 1,..., m), де m_ij = 1, якщо вершина v_i та ребро e_i, інцидентні, m_ij = 0 у протилежному випадку.

Приклад 3.14. Для неорієнтованого графа, зображеного на рис. 3.14, матриця інцидентності має вигляд

Отже, для простого графа в матриці інцидентності в кожному стовпці точно дві одиниці, і немає однакових стовпців. Матрицю інцидентності можна використовувати й для подання мультиграфа. Тоді з'являться однакові стовпці (вони відповідають кратним ребрам). Для подання псевдографа, якщо в ньому є петлі, у відповідних позиціях матриці ставимо 2 (у цьому разі матриця інцидентності не булева).

За допомогою матриці інцидентності можна подавати й орієнтовані графи. Для таких графів вона також не булева. Нехай G = (V, E) — орієнтований граф із множиною вершин V={v₁,v ₂,..., v_n } і множиною дуг Е= {е₁ е₂,..., е_т). Матрицею інцидентності орієнтованого графа G, яка відповідає заданій нумерації вершин і дуг, називають п×т матрицю М з елементами m_ij (і = 1,..., п; j = 1,..., m), де

Приклад 3.15. Для орієнтованого графа, зображеного на рис. 3.15, матриця інцидентності має вигляд

З алгоритмічного погляду матриця інцидентності — це, мабуть, найгірший спосіб подання графа, який тільки можна собі уявити [23]. По-перше, для цього потрібно п×т комірок пам'яті, більшість із яких зайняті нулями. По-друге, доступ до інформації незручний. Щоб отримати відповідь на елементарні питання (наприклад, чи існує дуга (v_i, v_j ), до яких вершин ведуть дуги з v_i), у найгіршому випадку потрібно перебрати всі стовпці матриці, тобто виконати т кроків.

Матриця суміжності

Нехай G = (V, Е) — простий граф, │v│ =п. Припустимо, що вершини графа G занумеровані: v₁ v₂, -, v„. Матрицею суміжності графа G (яка відповідає даній нумерації вершин) називають булеву п×п матрицю А з елементами a_ij (i,j= 1,..., п), де

 

 

Приклад 3.16. Матриця суміжності для графа, зображеного на рис. 3.14, має вигляд

Цілком очевидно, що для неорієнтованого графа a_ij = a_ji, тобто матриця суміжності симетрична. Більше того, позаяк у простому графі немає петель, то для нього в матриці суміжності a_ii = 0 (I = 1,..., п).

Матрицю суміжності можна використовувати також для подання псевдографа. Тоді це не булева матриця: елемент а_ij дорівнює кількості ребер, що з'єднують v_t та v_j. Петлю у вершині v_i подають значенням діагонального елемента а_й = 1. Для подання орієнтованих графів також використовують матрицю суміжності. Це булева п×п матриця А з елементами а_ij (i,j= 1,..., п), де

 

Приклад 3.17. Матриця суміжності для графа, зображеного на рис. 3.15, має вигляд.

Зазначимо, що матриця суміжності орієнтованого графа, загалом кажучи, несиметрична.

Матрицю суміжності можна використовувати й для подання орієнтованого мультиграфа. У такому разі це не булева матриця: елемент a_ij дорівнює кількості дуг, які мають v_i початковою вершиною, а v _j — кінцевою.

Велика перевага матриці суміжності як способу подання графа — швидкий доступ до інформації: за один крок можна одержати відповідь на питання, чи існує ребро (дуга) з v_i y v_j.Вада полягає в тому, що незалежно від кількості ребер обсяг пам'яті становить п² комірок. Як іще один аргумент проти використання матриці суміжності можна навести теорему про кількість кроків алгоритму, який на основі матриці суміжності перевіряє якусь властивість простого графа (див. підрозділ 3.5, теорему 3.9).

Нарешті, розглянемо ще два способи подання графів у пам'яті комп'ютера. Будь-яку скінченну послідовність довільних елементів будемо називати списком, а кількість елементів списку — його довжиною.