Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства вершин и ребер графа.Содержание книги
Поиск на нашем сайте
Определение 1. Ребра, имеющие одинаковые концевые точки называется параллельными
Определение 2. Ребро, концевые вершины которого совпадают, называется петлей
Определение 3. Вершина и ребро называются инцидентным друг другу, если вершина является для этого ребра концевой точкой Определение 4. Две вершины, являющиеся концевыми для некоторого ребра, называются смежными
Определение 5. Два ребра, инцидентные одной и той же вершине называется смежными ребрами
Определение 6. Степенью вершины называется число ребер, инцидентных ей: Пример:
Теорема. В графе G сумма степеней всех его вершин - число четное, равное удвоенному числу ребер.
Пример:
Определение 7. Граф называется полным, если любые две его различные вершины соединены ребром, и он не содержит параллельных ребер.
Определение 8. Дополнением графа G называется граф Пример: Построить полный граф для пяти вершин (n=5), число ребер равно 1. 2.
Пути и циклы графа. Определение 1. Путем в графе называется такая последовательность ребер (дуг), ведущей от начала вершины Например, на графе от
Определение 2. Циклом называется путь, начало, и конец которого совпадают:
Определение 3. Цикл называется простым, если он не проходит ни через одну вершину графа более одного раза.
Теорема. Для того чтобы граф представлял собой простой цикл, необходимо и достаточно, чтобы каждая его вершина имела степень равную двум, т.е.
Определение 4. Граф называется связным, если для любых двух его вершин существует соединяющий их путь, в противном случае граф - не связный:
Определение 5. В общем случае несвязный граф является совокупностью связных графов, называемых компонентами.
§4. Способы задания графа.
Существует ряд способов задания графов. Для решения конкретной задачи можно выбрать тот или иной способ, в зависимости от удобства его применения. Граф может быть задан: Рисунком. 2. Перечислением вершин и ребер:
Матрицей. Пример: Пусть граф G имеет 4 вершины и 4 ребра, т.е. 1) Рисунком: 2) Перечислением вершин и ребер:
3 ) Матрицей:
a) для неориентированного графа обычно задают матрицу смежности, элементы которой находятся по формуле:
b) для ориентированных графов задается матрица инцидентности, элементы которой находят по формуле:
Замечание: Граф может быть задан и матрицей с весами на ребрах: - если матрица симметричная, то граф неориентированный, - если матрица несимметричная, то граф ориентированный.
Деревья.
В экономике используется два вида графов: деревья и сети. Определение 1. Граф
Определение 2. Связный граф, не содержащий циклов, называется деревом, т.е. деревом графа является его связный подграф без цикла (не обязательно все вершины связны). Дерево имеет исходную вершину, называемую корнем и крайние вершины. Пути от исходной вершины к крайним называются ветвями. Несколько деревьев образуют несвязный граф - лес.
Определение 3. Дерево графа, содержащее все его вершины, называется покрывающим деревом или остовом.
Теорема 1. Граф G является деревом тогда и только тогда, когда он не содержит циклов и при соединении ребром произвольных двух его не смежных вершин получается граф, имеющий ровно один цикл.
Теорема 2. Граф G с «n» - вершинами является деревом тогда и только тогда, когда G - не связный граф и число ребер его равно (n-1).
|
|||||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 1058; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.106.49 (0.009 с.) |

 .
. .
. .
.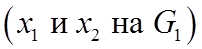 .
. .
. , причем, если
, причем, если  , то вершина называется висячей
, то вершина называется висячей 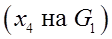 , если
, если  , то вершина называется изолированной
, то вершина называется изолированной  .
.


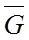 с теми же вершинами, что и граф G и содержащий только те ребра, которые надо добавить графу G, чтобы получился полный граф.
с теми же вершинами, что и граф G и содержащий только те ребра, которые надо добавить графу G, чтобы получился полный граф. .
.



 в конечную вершину
в конечную вершину  , в которой каждые два соседних ребра имеют общую вершину, и никакое ребро не встречается два раза, т.е. такая последовательность дуг, при которой конец одной дуги является началом другой.
, в которой каждые два соседних ребра имеют общую вершину, и никакое ребро не встречается два раза, т.е. такая последовательность дуг, при которой конец одной дуги является началом другой. :
: до
до 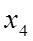


 .
.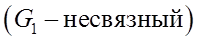 ,
,  .
.
 ,
, 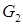 ,
,  - компоненты графа G.
- компоненты графа G.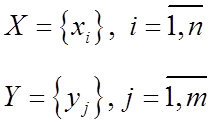 .
. и
и  . Задать граф можно:
. Задать граф можно: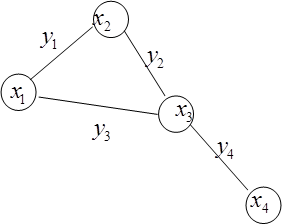





 Пример: Построить матрицу инцидентности для графа:
Пример: Построить матрицу инцидентности для графа:
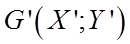 называется подграфом графа
называется подграфом графа 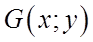 , если
, если 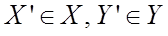 , причем ребро содержится в
, причем ребро содержится в 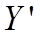 только в том случае, если его концевые вершины содержатся в
только в том случае, если его концевые вершины содержатся в 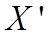 .
.