
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Центральные и вписанные углыСодержание книги
Поиск на нашем сайте
Вписанный угол (ACB) ― угол, вершина которого лежит на окружности, а стороны являются ее хордами: · измеряется половиной дуги, на которую он опирается; · вписанные углы, опирающиеся на одну и ту же дугу, равны; · вписанный угол, опирающийся на диаметр — прямой. Центральный угол (AOB) ― угол, образованный двумя радиусами: · измеряется дугой, на которую опирается; · центральный угол в два раза больше вписанного, опирающегося на ту же дугу.
Хорды и секущие Произведение длин отрезков пересекающихся хорд равны: · если хорды АВ и СD пересекаются в точке М, то АМ ВМ = СМ DМ.
Произведение длин отрезков секущей равно квадрату длины отрезка касательной: · если через точку М проведена секущая к окружности и касательная, причем точки А и В ― точки пересечения окружности с секущей, а С ― точка касания, то АМ ВМ = СМ 2.
Длина окружности и дуги Длина окружности: L = 2 πR = πD, R ― радиус окружности, D ― диаметр. Длина дуги окружности: l =
Площадь круга и сектора
Сектор — часть круга, ограниченная двумя радиусами и дугой окружности. Sкруга = πR 2 Sсектора =
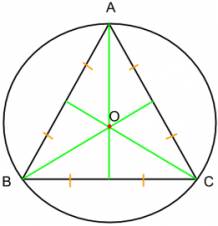
Комбинации с окружностью 1. Окружность называется вписанной в многоугольник, если все его стороны касаются окружности. 2. Центром вписанной окружности является точка пересечения биссектрис. 3. Центром описанной окружности является точка пересечения серединных перпендикуляров.
4. В любой треугольник можно вписать окружность, около любого треугольника можно описать окружность. 5. Радиус вписанной окружности в треугольнике: r = 6. Радиус описанной окружности в треугольнике: R = 7. В четырехугольник можно вписать окружность, если суммы противоположных сторон равны. 8. Вокруг четырехугольника можно описать окружность, если сумма противоположных углов равна 180°. 9. Из всех параллелограммов окружность можно вписать только в ромб и квадрат. 10. Из всех параллелограммов окружность можно описать только около прямоугольника и квадрата.
Равнобедренный треугольник В различных разделах математики существуют «звёзды» ― например, уже хорошо известное вам число пи или квадратные уравнения. Свои звёзды есть и среди треугольников ― это равнобедренный, равносторонний и прямоугольный треугольники, соответственно. Сейчас мы про них и поговорим.
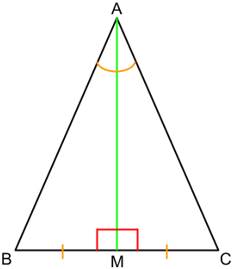
Итак, начнём с равнобедренного треугольника. Равнобедренный треугольник ― это треугольник, у которого две стороны равны (на нашем рисунке АВ = АС). Равные стороны в таком треугольнике называются боковыми (АВ и АС), а оставшаяся третья сторона ― основанием (ВС, соответственно). Естественно, он попал в список наших «звёзд» неслучайно ― у него есть ряд очень удобных свойств. Например, в равнобедренном треугольнике углы при основании равны (углы АВС и АСВ).
Кроме того, в равнобедренном треугольнике медиана, проведённая к основанию, является биссектрисой и высотой. То есть она не только делит противолежащую сторону пополам (ВМ = МС), но и падает на неё под углом 90°, а кроме того делит угол, из которого выходит, пополам (углы ВАМ и МАС равны).
Посмотрим на пример конкретной задачи. В равнобедренном треугольнике внешний угол равен 80°, необходимо найти все углы треугольника. Сразу возникает вопрос ― внешний угол при каком угле треугольника? Предположим, что это внешний угол при угле В (с нашего первого рисунка). Но в таком случае выходит, что сам ∠ В = 100° (по сумме смежных углов). Значит, и ∠ С = 100°, так как треугольник равнобедренный. Но тогда сумма только двух углов получается 200°, чего быть никак не может. Значит, речь идёт о внешнем угле при угле А треугольника. Тогда ∠ А = 100°, а ∠ В = ∠ С = 40°.
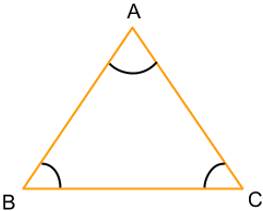
Равносторонний треугольник После знакомства с равнобедренным треугольником имеет смысл поближе узнать его близкого родственника ― равносторонний треугольник. Равносторонний треугольник ― это треугольник, у которого все три стороны равны. Кроме равенства сторон в таком треугольнике равны и все углы (каждый из которых по 60° ― так как 180°: 3 = 60°).
Если проводить аналогию с равнобедренным треугольником, в равностороннем любая сторона одновременно является и основанием, и боковой стороной. За счёт этого, в равностороннем медиана, проведённая из любого угла, будет являться биссектрисой и высотой (другими словами, равносторонний треугольник с любой стороны является равнобедренным).
Прямоугольный треугольник Особняком стоит наш третий гость ― прямоугольный треугольник. В отличие от первых двух, он не определяется равенством сторон. Зато в таком треугольнике один угол всегда равен 90° (собственно, это и есть прямой угол, дающий название всему треугольнику). Сторона, лежащая против такого угла, называется гипотенузой (сторона АВ на нашем рисунке), а две другие стороны ― катетами (АС и ВС, соответственно). Естественно, в любом прямоугольном треугольнике гипотенуза всегда больше катета (не забываем о том, что против большего угла лежит большая сторона, и наоборот).
Прямоугольный треугольник тоже обладает рядом замечательных свойств. К примеру, именно для него верна знаменитая теорема Пифагора (квадрат гипотенузы равен сумме квадратов катетов, или, по примеру нашего рисунка, АВ 2= АС 2 + ВС 2). Центр описанной вокруг прямоугольного треугольника окружности всегда лежит на гипотенузе (что несложно доказуемо, так как в этом случае прямой угол С становится вписанным, а против вписанного угла в 90° всегда лежит диаметр ― значит, гипотенуза является диаметром). Кроме того, у прямоугольного треугольника существует ещё ряд более мелких, но не менее важных свойств, которые вам предстоит узнать в процессе курса. Стоит ещё отметить такой нюанс: существует равнобедренный прямоугольный треугольник, своеобразный гибрид. В таком треугольнике катеты равны (так как равенства катета и гипотенузы не может быть, не забываем об этом), а все углы легко считаются ― раз один угол 90°, то два оставшихся угла получаются по 45°. Таким образом, вы успешно познакомились с тремя “особыми треугольниками”, так часто встречающимися в геометрии. В процессе курса вы узнаете о них гораздо больше, а пока имеет смысл закрепить полученные знания в домашнем задании.
Параллелограммы Мы уже успели познакомиться с особыми треугольниками, самое время поближе узнать “звёзд” среди четырёхугольников ― параллелограммы и их вариации. Сегодня мы будем говорить о самом параллелограмме, ромбе, прямоугольнике и квадрате. Начнём, естественно, с параллелограмма. Параллелограмм ― это четырёхугольник, у которого противоположные стороны параллельны (АВ || CD, AC || BD). У параллелограмма есть ряд замечательных свойств, которые и делают его таким особенным. В любом параллелограмме противоположные стороны равны (АВ = СD, AC = BD).
Кроме того, в параллелограмме противоположные углы равны (∠ А = ∠ D, ∠ B = ∠ C), а из параллельности сторон можно говорить и о равенстве частей углов (например, ∠ DAB = ∠ ADC; ∠ BCD = ∠ ABC). Ещё одно крайне полезное свойство ― диагонали параллелограмма точкой пересечения делятся пополам (АО = OD, CO = OB). У параллелограмма есть ряд частных случаев, которые не менее интересны, чем он сам. Например ― прямоугольник. Прямоугольник ― это параллелограмм, у которого все углы прямые. Кроме свойств параллелограмма, у прямоугольника есть и несколько своих. Диагонали прямоугольника равны (AD = BC), а стороны прямоугольника являются его высотами.
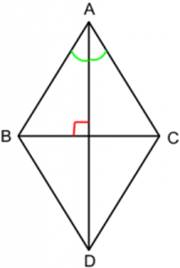
Ромб ― это параллелограмм, у которого все стороны равны. Естественно, ромбу присущи все те же свойства, что и параллелограмму. Вдобавок, диагонали ромба являются биссектрисами его углов и пересекаются под прямым углом (AD ⊥ BC). Интересно, что само слово “ромб” происходит от древнегреческого “бубен”, потому что в те времена бубны делали именно в форме бубна или квадрата.
И раз уж мы упомянули квадрат, то давайте поговорим о нём чуть подробнее. Квадрат ― это параллелограмм, у которого все стороны равны и все углы равны (AB = BC = CD = DA и ∠ A = ∠ B = ∠ C = ∠ D = 90°). Центры вписанной и описанной окружностей квадрата совпадают и одновременно являются точкой пересечения диагоналей (т. О). Стоит отметить, что любой квадрат является ромбом и прямоугольником, но не любой ромб или прямоугольник является квадратом.
Обратите внимание, что мы определяли каждую из фигур через предыдущую. И это сделано не просто так. Определение «Квадрат ― это параллелограмм, у которого все стороны равны и все углы равны», означает в том числе, что всё, что мы говорили в связи с параллелограммом, верно и для квадрата. А так как квадрат сочетает в себе признаки ромба и прямоугольника, то он обладает также и их свойствами. Поздравляем! Теперь вы знакомы не только с особыми треугольниками, но и с различными интересными четырёхугольниками. Гораздо подробнее о них (а также их свойствах) вы узнаете на лекциях, а сейчас имеет смысл отточить знания на проверочных заданиях.
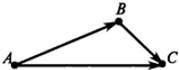
Векторы Сложение двух векторов Сумма двух векторов находится с помощью правила треугольника или правила параллелограмма: Правило треугольника:
Правило параллелограмма:
Для любых трех точек А, В, С справедливо соотношение:
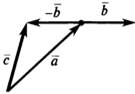
Вычитание векторов Разность двух векторов
Вектор
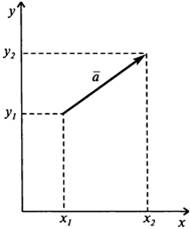
Координаты вектора · Координатами вектора называются разности координат конца и начала вектора. Координаты вектора не изменяются при параллельном переносе. У равных векторов соответствующие координаты равны. На плоскости:
Координаты вектора Модуль вектора: | В пространстве:
Координаты вектора Модуль вектора: |
|
|||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1132; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.71.60 (0.01 с.) |




 =
= 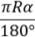 , α ― градусная мера дуги.
, α ― градусная мера дуги.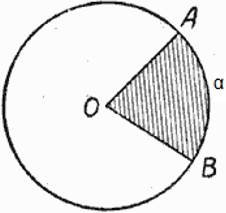
 , α ― градусная мера дуги.
, α ― градусная мера дуги.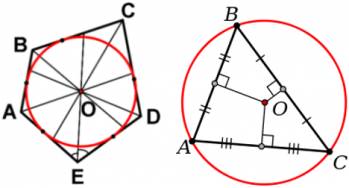
 , p ― полупериметр треугольника.
, p ― полупериметр треугольника.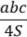 .
.




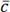 =
=  +
+ 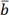 .
.
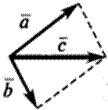
 +
+  =
= 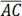 .
.

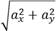 .
.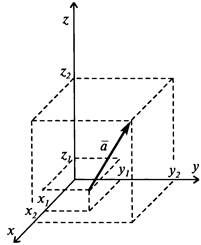
 (аx; ay; az): аx = x 2 – x 1; ay = y 2 – y 1; az = z 2 – z 1.
(аx; ay; az): аx = x 2 – x 1; ay = y 2 – y 1; az = z 2 – z 1.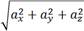 .
.


