
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графики элементарных функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Производная функции Производная описывает поведение функции на некотором ее участке (по производной проверяют возрастает функция на промежутке или убывает). Таким образом, смысл производной ― изучить функцию, найти ее экстремумы (максимум/минимум). Формулы нахождения производных основных функций:
Говоря совсем просто, для того чтобы найти производную функции, нужно по определенным правилам превратить её в другую функцию. Посмотрите еще раз на таблицу производных ― там функции превращаются в другие функции. Единственным исключением является экспоненциальная функция y = ex, которая «превращается» сама в себя. Рассмотрим следующие правила нахождения производных: 1) Постоянное число можно вынести за знак производной (Cu)′ = Cu ′, где C ― постоянное число. Пример: Найти производную функции y = 3cos x. y ′ = (3cos x)′. Смотрим в таблицу производных. Производная косинуса там есть, но у нас 3cos x. Выносим постоянный множитель за знак производной: y ′ = (3cos x)′ = 3(cos x)′ = 3(–sin x) = –3sin x. 2) Производная суммы равна сумме производных (u ± v)′ = u ′ ± v ′. Пример: Найти производную функции y = 6 + x + 3 x 2 – sin x – 23√ x + Применяем второе правило: y ′ = Все функции, находящиеся под штрихами, являются элементарными табличными функциями, с помощью таблицы осуществляем превращение: 0 + 1 + 3 ∙ 2 x – cos x – 2 ∙ Упростим выражение: 1 + 6 x – cos x – 3) Производная произведения функций (uv)′ = u ′ v + uv ′. Пример: Найти производную функции y = x 3arcsin x. Здесь у нас произведение двух функций, зависящих от x. Сначала применяем правило произведения, а затем превращаем функции по таблице производных: y ′ = (x 3arcsin x)′ = (x 3)′arcsin x + x 3(arcsin x)′ = 3 x 2arcsin x + x 3 ∙ 4) Производная частного функций Пример: Найти производную функции y =
y ′ = В данном случае замечаем множитель, который согласно первому правилу целесообразно вынести за знак производной: y ′ = Смотрим на наше выражение в скобках. У нас есть сложение, вычитание и деление. Со школы мы помним, что деление выполняется в первую очередь. И сначала применяем правило дифференцирования частного: y ′ = Пример: Найти производную функции y = Превратим нашу дробь в произведение, для этого поднимем экспоненту в числитель, сменив у показателя знак: y = Произведение дифференцировать проще: y ′ = (xex)′ = (x)′ ex + x (ex)′ = 1 ex + xex = ex (x + 1). 5) Производная сложной функции (u (v))′ = u ′(v) ∙ v ′. Прежде всего, обратим внимание на запись u (v). Здесь у нас две функции ― u и v, причем функция v, образно говоря, вложена в функцию u. Функция такого вида (когда одна функция вложена в другую) и называется сложной функцией. Пример: Найти производную функции y = sin(3 x – 5). Под синусом у нас находится не просто x, а целое выражение 3 x – 5, поэтому найти производную сразу по таблице не получится. Также мы замечаем, что здесь невозможно применить первые четыре правила. Первый шаг, который нужно выполнить при нахождении производной сложной функции состоит в том, чтобы разобраться, какая функция является внутренней, а какая ― внешней. В данном примере интуитивно понятно, что функция y = sin(3 x – 5) ― сложная функция, причем многочлен 3 x – 5 является внутренней функцией (вложением), а sin(3 x – 5) ― внешней функцией. В случае простых примеров вроде sin(3 x – 5) понятно, что под синус вложен многочлен 3 x – 5. А как же быть, если всё не очевидно? Как точно определить, какая функция является внешней, а какая внутренней? Для этого можно использовать следующий простой прием, который можно проводить мысленно или на черновике. Представим, что нам нужно вычислить на калькуляторе значение выражения sin(3 x – 5) при x = 1 (вместо единицы может быть любое число). Что мы вычислим в первую очередь? В первую очередь нужно будет выполнить следующее действие: 3 ∙ 1 – 5 = –2, поэтому многочлен 3 x – 5 и будет внутренней функцией v: y = sin Во вторую очередь нужно будет найти sin(–2), поэтому синус ― будет внешней функцией: y = Теперь применяем правило дифференцирования сложной функции (u (v))′ = u ′(v) ∙ v ′.
y ′ = (sin(3 x – 5))′; u ′(v) = cos(3 x – 5). Обратите внимание, что внутренняя функция v = 3 x – 5 не изменилась, её мы не трогаем. v ′ = (3 x – 5)′. Результат применения формулы (u (v))′ = u ′(v) ∙ v ′ в чистовом оформлении выглядит так: y ′ = (sin(3 x – 5))′ = cos(3 x – 5)(3 x – 5)′. Далее мы берем производную внутренней функции: y ′ = (sin(3 x – 5))′ = cos(3 x – 5)(3 x – 5)′ = cos(3 x – 5)(3 – 0) = 3cos(3 x – 5).
Графики Комбинации с окружностью Метод рационализации Метод «рационализации» заключается в замене сложного выражения F (x) на более простое выражение G (x), при которой неравенство G (x) ˅ 0 равносильно неравенству F (x) ˅ 0 в области определения выражения F (x). В таблице представлены некоторые выражения F и соответствующие им рационализирующие выражения G, в которых f, g, h, p, q ― выражения с переменной x (h > 0; h ≠ 1; f > 0; g > 0) и а ― фиксированное число (a > 0; a ≠ 1).
Некоторые следствия (с учетом области определения): log hf ∙ log pq ˅ 0 ⇔ (h – 1)(f – 1)(p – 1)(q – 1) ˅ 0; log hf ∙ log pg ˅ 0 ⇔ (fg – 1)(h – 1) ˅ 0; √ f – √ g ˅ 0 ⇔ f – g ˅ 0;
Неравенства Мы уже познакомились с рациональными уравнениями, формулами сокращённого умножения и тождествами в целом. У них существует младшие братья ― неравенства. Но, в отличие от старших братьев, младших зачастую недолюбливают и относятся к ним настороженно. Хотя, если знать правильный подход, общение с ними может стать лёгким и непринуждённым. Но вначале ― официальное знакомство. Неравенства могут обозначаться четырьмя способами: · > (читается как “больше”). Пример: х > 2. В этом случае решением будут любые х, большие двух (то есть от двух до плюс бесконечности, не включая 2). · < (читается как “меньше”). Пример: х < 9. В этом случае решением будут любые х, меньшие девяти (то есть от минус бесконечности до девяти, не включая девять). · ≥ (читается как “больше или равно”). Пример: x ≥ 5. В этом случае решением будут любые х, большие или равные пяти (то есть от пяти и до плюс бесконечности, включая пять). · ≤ (читается как “меньше или равно”). Пример: х ≤ 11. В этом случае решением будут любые х, меньшие или равные одиннадцати (то есть от минус бесконечности и до 11, включая 11). Наверняка вы уже успели заметить важное отличие первых двух типов неравенств. Подобные неравенства называются строгими ― они очень критично относятся к окружающим, и поэтому не включают в решение значение, относительно которого строятся (в наших примерах это числа 2 и 9, соответственно). В свою очередь, два оставшихся типа неравенств являются нестрогими и с удовольствием берут в решение и те точки, относительно которых строятся они (в наших примерах это точки 5 и 11, соответственно). Раз мы узнали поближе обычные неравенства, то стоит сказать пару слов и про двойные неравенства. Если просто неравенства накладывают условия только с одной стороны (или, если давать геометрическую интерпретацию, представляют из себя луч), то двойные неравенства вносят ограничения с двух сторон (и геометрически являются отрезком). Естественно, включение или не включение границы луча (в случае обычного неравенства) или границ отрезка (в случае двойного неравенства) зависит от строгости или нестрогости неравенств.
Пример: 4 < х ≤ 12. Решением такого неравенства будут любые значения х от четырёх (не включая четвёрку) и до 12 (включая двенадцать). Теперь самое время поговорить о тех самых правилах, которые облегчат ваше общение с неравенствами. Вот они: · В одиночных и двойных неравенствах можно прибавить/отнять слева и справа одинаковое число, а также умножить/разделить на любое положительное число. От таких процедур знак неравенства не изменится. Пример: 12 х – 5 < 7; 12 х – 5 + 5 < 7 + 5; 12 х < 12; х < 1. · При умножении/делении на отрицательное число знак неравенства меняется на противоположный. Пример: –7 х < 14; – х < 2; x > –2. · В неравенствах (как и в тождествах) можно переносить переменные/числа из одной стороны в другую. Не забывайте при этом менять знак переменных/чисел (но не неравенства!). Пример: х + 5 > 0; х > –5. Вот и всё! Следуя этим трём правилам, можно добиться отличного взаимопонимания с простейшими неравенствами, а впоследствии и с их сложными вариациями. Очень важно закрепить полученные знания на проверочных заданиях. До встречи на следующем уроке!
Окружность и круг Из всех фигур в геометрии, круг ― самая необычная фигура, ведь здесь нам постоянно приходится говорить о бесконечности, что определенно добавляет таинственности этой фигуре. Например, в треугольнике очень легко посчитать количество сторон, количество высот, количество биссектрис, в окружности же количество радиусов ― бесконечность, количество диаметров ― бесконечность, количество касательных ― бесконечность. Возможно, именно поэтому ученики так не любят задания с окружностью. Но все не так страшно. Чтобы справиться с этой таинственностью, достаточно знать ряд основных теорем, которые вы найдете в этом блоке. Начнем с определения фигуры и ее основных элементов. Окружность ― множество всех точек плоскости, равноудаленных от данной точки на плоскости (то есть замкнутая линия). Круг ― часть плоскости, ограниченная окружностью (то есть площадь).
Элементы окружности
Центр окружности ― точка O. Радиус окружности (r) ― отрезок, соединяющий точку окружности с центром. Все радиусы одной окружности равны. Хорда (AB) ― отрезок, соединяющий любые две точки окружности. Диаметр (d) ― хорда, проходящая через центр окружности. Диаметр равен двум радиусам.
Касательная к окружности Касательная ― прямая, имеющая с окружностью ровно одну общую точку.
Хорды и секущие Произведение длин отрезков пересекающихся хорд равны: · если хорды АВ и СD пересекаются в точке М, то АМ ВМ = СМ DМ.
Произведение длин отрезков секущей равно квадрату длины отрезка касательной: · если через точку М проведена секущая к окружности и касательная, причем точки А и В ― точки пересечения окружности с секущей, а С ― точка касания, то АМ ВМ = СМ 2.
Длина окружности и дуги Длина окружности: L = 2 πR = πD, R ― радиус окружности, D ― диаметр. Длина дуги окружности: l =
Площадь круга и сектора
Сектор — часть круга, ограниченная двумя радиусами и дугой окружности. Sкруга = πR 2 Sсектора =
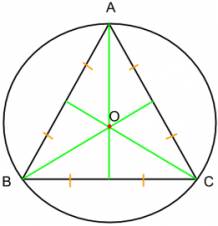
Комбинации с окружностью 1. Окружность называется вписанной в многоугольник, если все его стороны касаются окружности. 2. Центром вписанной окружности является точка пересечения биссектрис. 3. Центром описанной окружности является точка пересечения серединных перпендикуляров.
4. В любой треугольник можно вписать окружность, около любого треугольника можно описать окружность. 5. Радиус вписанной окружности в треугольнике: r = 6. Радиус описанной окружности в треугольнике: R = 7. В четырехугольник можно вписать окружность, если суммы противоположных сторон равны. 8. Вокруг четырехугольника можно описать окружность, если сумма противоположных углов равна 180°. 9. Из всех параллелограммов окружность можно вписать только в ромб и квадрат. 10. Из всех параллелограммов окружность можно описать только около прямоугольника и квадрата.
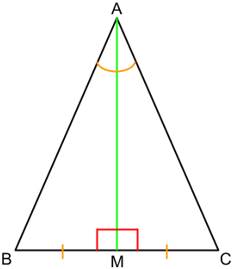
Равнобедренный треугольник В различных разделах математики существуют «звёзды» ― например, уже хорошо известное вам число пи или квадратные уравнения. Свои звёзды есть и среди треугольников ― это равнобедренный, равносторонний и прямоугольный треугольники, соответственно. Сейчас мы про них и поговорим. Итак, начнём с равнобедренного треугольника. Равнобедренный треугольник ― это треугольник, у которого две стороны равны (на нашем рисунке АВ = АС). Равные стороны в таком треугольнике называются боковыми (АВ и АС), а оставшаяся третья сторона ― основанием (ВС, соответственно). Естественно, он попал в список наших «звёзд» неслучайно ― у него есть ряд очень удобных свойств. Например, в равнобедренном треугольнике углы при основании равны (углы АВС и АСВ).
Кроме того, в равнобедренном треугольнике медиана, проведённая к основанию, является биссектрисой и высотой. То есть она не только делит противолежащую сторону пополам (ВМ = МС), но и падает на неё под углом 90°, а кроме того делит угол, из которого выходит, пополам (углы ВАМ и МАС равны).
Посмотрим на пример конкретной задачи. В равнобедренном треугольнике внешний угол равен 80°, необходимо найти все углы треугольника. Сразу возникает вопрос ― внешний угол при каком угле треугольника? Предположим, что это внешний угол при угле В (с нашего первого рисунка). Но в таком случае выходит, что сам ∠ В = 100° (по сумме смежных углов). Значит, и ∠ С = 100°, так как треугольник равнобедренный. Но тогда сумма только двух углов получается 200°, чего быть никак не может. Значит, речь идёт о внешнем угле при угле А треугольника. Тогда ∠ А = 100°, а ∠ В = ∠ С = 40°.
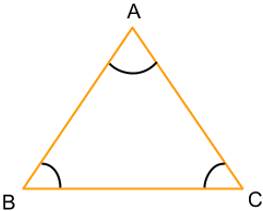
Равносторонний треугольник После знакомства с равнобедренным треугольником имеет смысл поближе узнать его близкого родственника ― равносторонний треугольник. Равносторонний треугольник ― это треугольник, у которого все три стороны равны. Кроме равенства сторон в таком треугольнике равны и все углы (каждый из которых по 60° ― так как 180°: 3 = 60°).
Если проводить аналогию с равнобедренным треугольником, в равностороннем любая сторона одновременно является и основанием, и боковой стороной. За счёт этого, в равностороннем медиана, проведённая из любого угла, будет являться биссектрисой и высотой (другими словами, равносторонний треугольник с любой стороны является равнобедренным).
Прямоугольный треугольник Особняком стоит наш третий гость ― прямоугольный треугольник. В отличие от первых двух, он не определяется равенством сторон. Зато в таком треугольнике один угол всегда равен 90° (собственно, это и есть прямой угол, дающий название всему треугольнику). Сторона, лежащая против такого угла, называется гипотенузой (сторона АВ на нашем рисунке), а две другие стороны ― катетами (АС и ВС, соответственно). Естественно, в любом прямоугольном треугольнике гипотенуза всегда больше катета (не забываем о том, что против большего угла лежит большая сторона, и наоборот).
Прямоугольный треугольник тоже обладает рядом замечательных свойств. К примеру, именно для него верна знаменитая теорема Пифагора (квадрат гипотенузы равен сумме квадратов катетов, или, по примеру нашего рисунка, АВ 2= АС 2 + ВС 2). Центр описанной вокруг прямоугольного треугольника окружности всегда лежит на гипотенузе (что несложно доказуемо, так как в этом случае прямой угол С становится вписанным, а против вписанного угла в 90° всегда лежит диаметр ― значит, гипотенуза является диаметром). Кроме того, у прямоугольного треугольника существует ещё ряд более мелких, но не менее важных свойств, которые вам предстоит узнать в процессе курса. Стоит ещё отметить такой нюанс: существует равнобедренный прямоугольный треугольник, своеобразный гибрид. В таком треугольнике катеты равны (так как равенства катета и гипотенузы не может быть, не забываем об этом), а все углы легко считаются ― раз один угол 90°, то два оставшихся угла получаются по 45°. Таким образом, вы успешно познакомились с тремя “особыми треугольниками”, так часто встречающимися в геометрии. В процессе курса вы узнаете о них гораздо больше, а пока имеет смысл закрепить полученные знания в домашнем задании.
Параллелограммы Мы уже успели познакомиться с особыми треугольниками, самое время поближе узнать “звёзд” среди четырёхугольников ― параллелограммы и их вариации. Сегодня мы будем говорить о самом параллелограмме, ромбе, прямоугольнике и квадрате. Начнём, естественно, с параллелограмма. Параллелограмм ― это четырёхугольник, у которого противоположные стороны параллельны (АВ || CD, AC || BD). У параллелограмма есть ряд замечательных свойств, которые и делают его таким особенным. В любом параллелограмме противоположные стороны равны (АВ = СD, AC = BD).
Кроме того, в параллелограмме противоположные углы равны (∠ А = ∠ D, ∠ B = ∠ C), а из параллельности сторон можно говорить и о равенстве частей углов (например, ∠ DAB = ∠ ADC; ∠ BCD = ∠ ABC). Ещё одно крайне полезное свойство ― диагонали параллелограмма точкой пересечения делятся пополам (АО = OD, CO = OB). У параллелограмма есть ряд частных случаев, которые не менее интересны, чем он сам. Например ― прямоугольник. Прямоугольник ― это параллелограмм, у которого все углы прямые. Кроме свойств параллелограмма, у прямоугольника есть и несколько своих. Диагонали прямоугольника равны (AD = BC), а стороны прямоугольника являются его высотами.
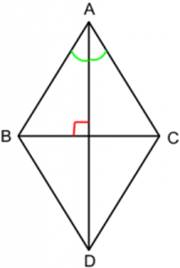
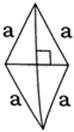
Ромб ― это параллелограмм, у которого все стороны равны. Естественно, ромбу присущи все те же свойства, что и параллелограмму. Вдобавок, диагонали ромба являются биссектрисами его углов и пересекаются под прямым углом (AD ⊥ BC). Интересно, что само слово “ромб” происходит от древнегреческого “бубен”, потому что в те времена бубны делали именно в форме бубна или квадрата.
И раз уж мы упомянули квадрат, то давайте поговорим о нём чуть подробнее. Квадрат ― это параллелограмм, у которого все стороны равны и все углы равны (AB = BC = CD = DA и ∠ A = ∠ B = ∠ C = ∠ D = 90°). Центры вписанной и описанной окружностей квадрата совпадают и одновременно являются точкой пересечения диагоналей (т. О). Стоит отметить, что любой квадрат является ромбом и прямоугольником, но не любой ромб или прямоугольник является квадратом.
Обратите внимание, что мы определяли каждую из фигур через предыдущую. И это сделано не просто так. Определение «Квадрат ― это параллелограмм, у которого все стороны равны и все углы равны», означает в том числе, что всё, что мы говорили в связи с параллелограммом, верно и для квадрата. А так как квадрат сочетает в себе признаки ромба и прямоугольника, то он обладает также и их свойствами. Поздравляем! Теперь вы знакомы не только с особыми треугольниками, но и с различными интересными четырёхугольниками. Гораздо подробнее о них (а также их свойствах) вы узнаете на лекциях, а сейчас имеет смысл отточить знания на проверочных заданиях.
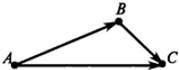
Векторы Сложение двух векторов Сумма двух векторов находится с помощью правила треугольника или правила параллелограмма: Правило треугольника:
Правило параллелограмма:
Для любых трех точек А, В, С справедливо соотношение:
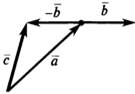
Вычитание векторов Разность двух векторов
Вектор
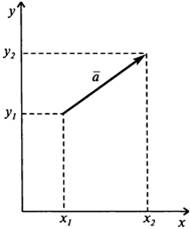
Координаты вектора · Координатами вектора называются разности координат конца и начала вектора. Координаты вектора не изменяются при параллельном переносе. У равных векторов соответствующие координаты равны. На плоскости:
Координаты вектора Модуль вектора: | В пространстве:
Координаты вектора Модуль вектора: | Треугольники Внешний угол треугольника
· δ — внешний угол треугольника, является смежным с одним из внутренних углов (сумма = 180°). Из этого следует, что внешний угол равен сумме двух внутренних, но не смежных с ним, углов треугольника (α+ β = δ). Стороны треугольника
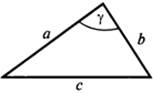
· Сумма длин двух любых сторон треугольника всегда больше длины третьей стороны (a + b > c). · Напротив большей стороны находится больший угол; напротив меньшего угла находится меньшая сторона. · Если a<b<c, то α<β<γ и наоборот. · Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Она параллельна основаниютреугольника и равна его половине.
· Теорема косинусов:с ² = а ² + b ² – 2 ab · cos γ.
· Теорема синусов: Признаки равенства треугольников:
· По двум сторонам и углу между ними.
· По одной стороне и двум прилегающим к ней углам.
· По трем сторонам. Равнобедренный треугольник
· В равнобедренном треугольнике боковые стороны равны, как и углы при основании. · Высота, опущенная на основание, является также биссектрисой (делит угол при вершине пополам) и медианой (делит основание пополам). · Угол при основании = · Угол при вершине = 180° – 2 (угол при основании). · Если в треугольнике совпадает любая пара отрезков из тройки медиана — биссектриса — высота, то треугольник равнобедренный. Равносторонний треугольник
В равностороннем треугольнике: · Все углы равны 60°. · Периметр треугольника = 3 а. · Площадь треугольника: · Точка пересечения высот, которые также являются биссектрисами и медианами, делит каждую из них в отношении 2: 1. · Точка пересечения высот также является центром вписанной и описанной окружностей. Прямоугольный треугольник
В прямоугольном треугольнике: · Один из углов = 90°; · Сумма остальных двух углов = 90°; · Гипотенуза является наибольшей стороной (находится напротив угла 90°); · Площадь треугольника: · Теорема Пифагора: сумма квадратов катетов равна квадрату гипотенузы a ² + b ² = c ²; · Если в треугольнике выполняется теорема Пифагора, то треугольник прямоугольный. Подобные треугольники
· Треугольники называются подобными, если их углы равны. В подобных фигурах сохраняется отношение между соответствующими сторонами другими линейными величинами (высоты, медианы, биссектрисы и периметры): · Также сохраняется внутреннее отношение длин: Четырехугольники Четырехугольник
· Сумма углов в любом четырехугольнике всегда равна 360°. · Периметр любого четырехугольника равен сумме его сторон.
· Площадь (через диагонали и угол между ними)S=
· Если соединить середины сторон четырехугольника отрезками, то получится параллелограмм, площадь которого равна половине площади четырехугольника.
· Четырехугольник можно вписать в окружность, если сумма противоположных углов равна 180°: α + γ = β + δ = 180°. · Если четырехугольник вписан в окружность, то сумма противоположных углов равна 180°. Параллелограмм
· Параллелограмм — четырехугольник, у которого противоположные стороны равны и параллельны. · У параллелограмма противоположные углы равны. · Сумма углов, лежащих на одной стороне равна180°: α + β = 180°. · Диагонали параллелограмма, делятся пополам в точке пересечения. · Периметр параллелограмма равен 2 a + 2 b. Площадь параллелограмма
· Через сторону и опущенную на нее высоту:S = aha = bhb.
· Через две прилежащие стороны и угол между ними:S = ab · sin α.
· Через диагонали и угол между ними:S= Прямоугольник
· Прямоугольник — параллелограмм, у которого все углы равны 90°. · Диагонали равны, в точке пересечения делятся пополам. · Периметр прямоугольника равен 2 a + 2 b. Площадь прямоугольника
· Через стороны:S = a · b. · Через диагональ и угол между диагоналями:S= Ромб
· Ромб — параллелограмм, у которого все стороны равны. · Диагонали ромба, не будучи равны друг другу, делятся пополам в точке пересечения; перпендикулярны и являются биссектрисами углов. · Периметр ромба равен 4 a. Квадрат
· Квадрат является параллелограммом, у которого все стороны и все углы равны между собой. · Каждый угол квадрата равен 90°. · Периметр квадрата равен 4 a. · Площадь квадрата со стороной a равна: а² или · Диагонали квадрата равны, в точке пересечения делятся пополам, являются биссектрисами углов квадрата и перпендикулярны друг другу. Трапеция
· Трапеция — четырехугольник, у которого две стороны параллельны, а две другие нет (α || β). · Сумма углов, прилегающих к боковой стороне, равна 180° (α + β = 180°).
· Средняя линия параллельна основаниям и равна их полусумме. Отрезок с концами, лежащими на основаниях трапеции, делится средней линией пополам. Равнобокая трапеция
· В равнобокой трапеции боковые стороны равны, углы при нижнем и при верхнем основании, а также диагонали равны.
Треугольники Внешний угол треугольника
· Δ— внешний угол треугольника, является смежным с одним из внутренних углов (сумма = 180°). Из этого следует, что внешний угол равен сумме двух внутренних, но не смежных с ним, углов треуг
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 762; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.219.241 (0.014 с.) |




 (ln x)′ =
(ln x)′ = 





 – 11ctg x.
– 11ctg x. = (6)′ + (x)′ + (3 x 2)′ – (sin x)′ –
= (6)′ + (x)′ + (3 x 2)′ – (sin x)′ –  + (x -2)′ – (11ctg x)′ = (6)′ + (x)′ + 3(x 2)′ – (sin x)′ –
+ (x -2)′ – (11ctg x)′ = (6)′ + (x)′ + 3(x 2)′ – (sin x)′ –  + (x -2)′ – 11(ctg x)′.
+ (x -2)′ – 11(ctg x)′. ∙
∙  + (–2) ∙ x -3 – 11 ∙
+ (–2) ∙ x -3 – 11 ∙  .
. –
–  +
+  .
. .
. =
=  .
. .
. .
. =
=  .
. =
=  =
=  =
= 
 .
. = xex.
= xex. .
. .
. ˅ 0 ⇔
˅ 0 ⇔  ˅ 0.
˅ 0.




 =
= 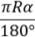 , α ― градусная мера дуги.
, α ― градусная мера дуги.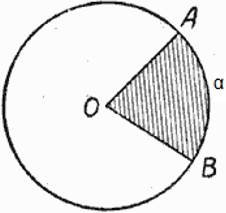
 , α ― градусная мера дуги.
, α ― градусная мера дуги.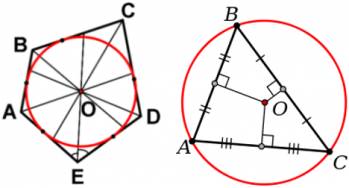
 , p ― полупериметр треугольника.
, p ― полупериметр треугольника.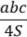 .
.




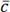 =
=  +
+ 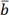 .
.
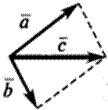
 +
+  =
= 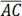 .
.

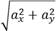 .
.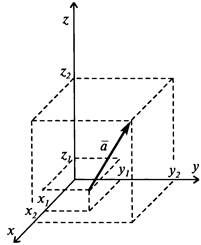
 (аx; ay; az): аx = x 2 – x 1; ay = y 2 – y 1; az = z 2 – z 1.
(аx; ay; az): аx = x 2 – x 1; ay = y 2 – y 1; az = z 2 – z 1.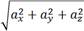 .
.


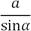 =
=  =
=  . Это отношение равно 2 R, где R — радиус описанной окружности.
. Это отношение равно 2 R, где R — радиус описанной окружности.



 .
.
 .
.
 =
=  ;
;
 =
=  =
=  =
=  .
. =
=  ;
;  =
=  .
.

 .
.





 .
.

 .
.

 .
.






