
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общее для всех треугольниковСодержание книги
Поиск на нашем сайте
Параллельные прямые и секущая
· Сумма углов в треугольнике равна α + β + γ = 180°.
· Периметр треугольника равен сумме его сторон: P = a + b + c. · h — высота в треугольнике. Высота — перпендикуляр, опущенный из вершины угла, лежащего против выбранной стороны, на выбранную сторону. Может находиться как внутри, так и вне треугольника.
· Площадь треугольника равна половине:
· Через две стороны и угол между ними: S = Внешний угол треугольника
· Δ— внешний угол треугольника, является смежным с одним из внутренних углов (сумма = 180°). Из этого следует, что внешний угол равен сумме двух внутренних, но не смежных с ним, углов треугольника (α + β = δ). Стороны треугольника
· Сумма длин двух любых сторон треугольника всегда больше длины третьей стороны (a + b > c). · Напротив большей стороны находится больший угол; напротив меньшего угла находится меньшая сторона. · Если a < b < c, то α < β < γ и наоборот. · Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Она параллельна основаниютреугольника и равна его половине.
· Теорема косинусов: с ² = а ² + b ² – 2 ab · cos γ.
· Теорема синусов: Признаки равенства треугольников:
· По двум сторонам и углу между ними.
· По одной стороне и двум прилегающим к ней углам.
· По трем сторонам. Равнобедренный треугольник
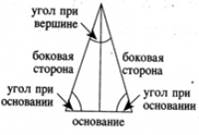
· В равнобедренном треугольнике боковые стороны равны, как и углы при основании. · Высота, опущенная на основание, является также биссектрисой (делит угол при вершине пополам) и медианой (делит основание пополам). · Угол при основании = · Угол при вершине = 180° – 2 (угол при основании). · Если в треугольнике совпадает любая пара отрезков из тройки медиана — биссектриса — высота, то треугольник равнобедренный. Равносторонний треугольник
В равностороннем треугольнике: · Все углы равны 60°. · Периметр треугольника = 3 а. · Площадь треугольника: · Точка пересечения высот, которые также являются биссектрисами и медианами, делит каждую из них в отношении 2: 1. · Точка пересечения высот также является центром вписанной и описанной окружностей. Прямоугольный треугольник
В прямоугольном треугольнике: · Один из углов = 90°; · Сумма остальных двух углов = 90°; · Гипотенуза является наибольшей стороной (находится напротив угла 90°); · Площадь треугольника: · Теорема Пифагора: сумма квадратов катетов равна квадрату гипотенузы a ² + b ² = c ²; · Если в треугольнике выполняется теорема Пифагора, то треугольник прямоугольный. Окружность, описанная около прямоугольного треугольника
Центр описанной окружности совпадает с серединой гипотенузы, а радиус равен: · половине гипотенузы: R = · медиане, проведенной к гипотенузе: R = mc. Подобные треугольники
· Треугольники называются подобными, если их углы равны. В подобных фигурах сохраняется отношение между соответствующими сторонами другими линейными величинами (высоты, медианы, биссектрисы и периметры): · Также сохраняется внутреннее отношение длин: Признаки подобия треугольников
· По двум пропорциональным сторонам и углу между ними:
· По двум равным углам.
· По трем пропорциональным сторонам:
Введение в прогрессии Арифметическая прогрессия Арифметической прогрессией называют такую числовую последовательность, каждый следующий член которой отличается от предшествующего члена на одно и тоже число d. Число d называют разностью арифметической прогрессии. Отметим, что если d > 0, то арифметическая прогрессия является возрастающей последовательностью, если d < 0, то — убывающей последовательностью. Если a 1 — первый член прогрессии, d — разность прогрессии, то справедливы следующие формулы: · an = a 1 + d ·(n −1) — формула n -го члена; · Sn = · an = Геометрическая прогрессия Геометрической прогрессией называют такую числовую последовательность, каждый член которой, начиная со второго, равен предшествующему члену, умноженному на одно и то же число q. Число q называют знаменателем геометрической прогрессии. Если b 1 — первый член прогрессии (b 1 ≠ 0), а q — знаменатель прогрессии (q ≠ 0), то справедливы следующие формулы: · bn = b 1 qn -1 формула n -го члена; · Sn = · bn = Если | q | < 1, то имеем бесконечную убывающую геометрическую прогрессию, сумму которой находят по формуле S =
Проценты
С процентами нам постоянно приходиться сталкиваться в повседневной жизни. “Скидка 30%”, “Кредит без процентов за 5 минут”, “Арендная плата выросла на 12%” ― со всех сторон на нас сыпятся рекламные слоганы и призывы. Но что же значит это таинственное слово “проценты”? И как ими оперировать?
Сегодня мы с вами дадим определение процентов, поймём, как находится процент от некоторого числа, как можно найти одно количество процентов, уже зная другое. И, конечно, рассмотрим каждый из этих случаев на конкретном примере.
Как кирка у каменщика, камертон у настройщика или световой меч у Джедая, в математике тоже существуют свои инструменты, нужные для выполнения тех или иных операций. И проценты как раз и являются таким удобным инструментом. Нужны они для нахождения части от чего-то. Вообще говоря, звучит похоже на определение дроби. И действительно, проценты очень тесно связаны с дробями, по сути, основываясь на них. Так что же такое один процент?
Один процент ― это одна сотая. 1% = 0,01.
Одна сотая чего бы то ни было ― территории леса, зарплаты, ткани, стоимости новых брюк. Переменной х или у. Если 1% = 0,01, то 100% = 1, то есть весь предмет (о котором идёт речь) целиком.
Пример: 1% территории музея составляют 20 м2. Какую территорию занимает музей? Пусть вся территория музея ― это х. Тогда один процент от х равен 20 ― или 0,01 х = 20. Отсюда с лёгкостью находится и весь размер музея: х = 2000 м2.
Ситуация несколько усложняется, когда изначально нам известен не 1%, а несколько ― например, 20. А требуют найти какое-нибудь неудобное число процентов.
Пример: 38% населения деревни ― это 76 человек. Сколько человек составляет 15% от общего населения? Так как мы не можем сразу найти 15%, то нам вначале понадобится сделать промежуточный шаг ― найти 1%. Если 38% ― это 76 человек, то, разделив на 38, мы получим так нужный нам 1%. 38% = 76 человек ⇒ 1% = 2 человека. Тогда 15% = 30 человек.
Но неугомонные математики не остановились и на этом. Что будет, если мы возьмём процент от какого-то числа, вычтем или прибавим к начальному числу, а затем снова возьмём то же количество процентов?
Пример: В 2010 дом стоял 2 тысячи рублей. В 2011 его цена увеличилась на 20%, а в 2012 ― ещё на 20%. Сколько дом стоил к концу 2012 года? На примере этой задаче мы посмотрим не только на то, как нужно брать проценты от разных величин, но и как переводить проценты в дроби. Решим её двумя способами. Способ 1. Для начала давайте выясним, сколько стоил дом в 2011. Его стоимость увеличилась на 20%, т. е. на 400 рублей (1% = 2000:100 = 20, 20% = 400) и стала, соответственно, равна 2400. Теперь нам нужно узнать, сколько он стал стоить в 2012. Важно! Сейчас мы будем брать 20% от новой цены, т.е. той, которая была на дом в 2011 году. Если 1% = 2400:100 = 24, то 20% = 480, то есть новая цена в 2012 году ― 2400 + 480 = 2880. Способ 2. Если 1% ― это 0,01 от чего-то, то 20% ― это 0,2. Тогда 20% от первоначальной цены это 2000 х 0,2 = 400, и цена на дом в 2011 году стала 2400. Теперь находим 20% от новой стоимости 2400 х 0,2 = 480 и итоговую стоимость в 2012 году: 2400 + 480 = 2880.
Отлично! Итак, мы не только узнали, что такое проценты, как можно с ними обращаться, но и выяснили, как можно брать проценты от разных величин и как сопоставлять проценты с дробями. Больше интересных фактов и приёмов работы с процентами вы узнаете в процессе курса, а сейчас ― самое время отработать новые знания в проверочных заданиях.
Равносильные системы
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 720; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.214.1 (0.007 с.) |




 =
= 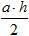 .
.
 ab · sin γ.
ab · sin γ.



 =
=  =
=  . Это отношение равно 2 R, где R — радиус описанной окружности.
. Это отношение равно 2 R, где R — радиус описанной окружности.


 .
.
 .
.
 =
=  ;
;
 ;
;
 =
=  =
=  =
=  .
. =
=  ;
;  =
=  .
.
 =
=  .
.

 =
=  =
=  .
. n и Sn =
n и Sn =  n — формулы суммы n первых членов;
n — формулы суммы n первых членов; (an −1 + an +1) — свойство n -го члена.
(an −1 + an +1) — свойство n -го члена. формула суммы n первых членов;
формула суммы n первых членов; свойство n -го члена.
свойство n -го члена. .
.


