
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Винтовые потоки (течения Бельтрами).Содержание книги Поиск на нашем сайте
КУРСОВАЯ РАБОТА по дисциплине «Геофизическая гидродинамика» на тему: «Анализ винтовых потоков в атмосфере Земли»
Выполнил: Кравцова А.С. студент 4 курса группы «ФИЗ-б-о-111» направления (специальности) Физика очной формы обучения ________________________ (подпись)
Руководитель работы: Шевченко А. И. доцент кафедры теоретической физики
Работа допущена к защите _______________________ ______________ (подпись руководителя) (дата)
Работа выполнена и защищена с оценкой _________________________ Дата защиты______________
Члены комиссии: зав.каф. тер.физики __________ Волкова В.И. доцент каф. тер.физики __________ Шевченко А.И. доцент каф. тер.физики __________ Смерек Ю.Л. доцент каф. тер.физики __________ Кульгина Л.М.
Ставрополь, 2014 г. Содержание Содержание………………………………………………………………………..2 Введение…………………………………………………………………………...3 1. Винтовые потоки (течения Бельтрами)……………………………………….4 1.1. Двумерные течения………………………………………………………..6 1.2. Одномерные течения…………………………………………………...…7 2. Исходные уравнения………………………………………………………….10 3. Уравнения для винтовых течений в декартовых, круговых цилиндрических и сферических координатах……………………………………………………..15 3.1. Декартовы и круговые цилиндрические координаты…………………15 3.2. Сферические координаты……………………………………………….17 4. Винтовые течения в сферических координатах при наличии осевой симметрии………………………………………………………………………..20 5. Поверхности тока вихрей первой и второй степени………………………..24 6. Винтовые потоки с винтовой симметрией поля течения…………………..27 Заключение……………………………………………………………………….29 Список используемой литературы……………………………………………...30
Введение. Основы теории винтовых потоков были заложены в 1881 г. И.С. Громекой в его малоизвестной диссертации "Некоторые случаи движения несжимаемой жидкости" и независимо в 1889 г. в более известной работе итальянского математика Бельтрами (по этой причине винтовые потоки известны еще как течения Бельтрами). Цель: Изучить винтовые потоки в атмосфере Земли. Задачи: · Рассмотреть винтовые потоки (течения Бельтрами); · Изучить исходные уравнения; · Рассмотреть уравнения для винтовых течений в декартовых, круговых цилиндрических и сферических координатах; · Рассмотреть винтовые течения в сферических координатах при наличии осевой симметрии; · Изучить поверхности тока вихрей первой и второй степени; · Изучить винтовые потоки с винтовой симметрией поля течения. · Двумерные течения. В общем случае в каждый момент времени поле скоростей потока жидкости определяется тремя функциями -
Поток, который может быть отнесен к такой координатной системе, что-бы все три компоненты скорости -
будем называть двумерным. Геометрически это означает, что на всех координатных поверхностях
Отсюда вытекает, что якобиан от составляющих скорости по координатам тождественно равен нулю
Следовательно, между функциями
которая позволяет одновременно с уменьшением числа переменных в уравнениях движения сократить число уравнений в системе. Одномерные течения. По аналогии с двумерными течениями одномерными потоками назовем течения, которые могут быть отнесены к такой координатной системе, в которой компоненты скорости будут функциями одной координаты
Очевидно, что все рассмотренные примеры двумерных течений в предположении (1.4) могут быть существенно упрощены. Из всего множества возможных случаев перехода от двумерных потоков к одномерным ограничимся рассмотрением двух важных примеров с постоянным распределением завихренности.
1. Пусть скорость плоскопараллельного установившегося течения в инерциальной системе координат имеет только одну составляющую
Отсюда
Это течение изображено на рис. 1.8 и называется сдвиговым течением. В частном случае (
2. Пусть имеется установившееся течение с постоянной величиной завихренности, которое в цилиндрической системе координат имеет только одну окружную составляющую
После интегрирования находим
Для течений с ограниченными скоростями константу Исходные уравнения. Система уравнений идеального изотермического газа применительно к атмосфере Земли в пренебрежении центробежной силой имеет следующий вид:
где Пусть течения однородные винтовые:
Здесь
Решая уравнение (5) относительно плотности, запишем
Как известно, для стандартной атмосферы в ее 70 - километровом (по толщине) слое абсолютная температура отличается от ее среднего значения не более, чем на 5 %</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
Следовательно, в выражении (2.6) множитель, включающий скорость, весьма мало отличается от единицы. В результате с погрешностью, не превышающей
Полагая, найдем. В результате будем иметь
С учетом выражения (2.9) уравнениям (2.2) и (2.4) придадим следующий вид:
Положим
где
Дальнейшее рассмотрение проведем в ортогональной системе координат
В работах при изучении однородных винтовых течений жидкости постоянной плотности (
Здесь Обобщая представление (2.15), будем разыскивать решение уравнения (2.13) в виде
где
Здесь штрих означает дифференцирование соответствующей величины по своему аргументу. Приравнивая в соотношении (2.17) нулю коэффициенты при
Далее для простоты положим s New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>=1. (2.22)</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> Тогда из соотношений (2.18) – (2.20) следует
Учтем выражения (2.22) – (2.25) в уравнении (2.21) и введем новый обобщенный потенциал
Здесь величина
Учитывая соотношения (1.22) – (1.26) в выражении для скорости (2.16), запишем
Таким образом, задача решения уравнения (2.13) в ортогональных координатах (2.14) сведена к линейному однородному дифференциальному уравнению в частных производных второго порядка (2.27), служащему для определения обобщенного потенциала S. Если этот обобщенный потенциал найден, то поле скорости определим с помощью выражения (2.28). Отметим, что среди приведенных в курсе ортогональных координатных систем, в которых переменные в уравнении (2.27) разделяются, условиям (2.14) удовлетворяют прямоугольная система В указанных прямоугольных и трех цилиндрических системах координат удобно положить
Здесь
В пренебрежении силой Кориолиса
Учитывая выражение (2.31) в уравнении неразрывности (2.10), получим следующее уравнение для потенциала Φ
Отметим, что в случае потенциальных течений выполнение условий (2.14) не обязательно. Pассмотрение проводилось в предположении, что температура T атмосферы не зависит от высоты (
Сферические координаты. В сферических координатах
Здесь
Учитывая, что толщина атмосферного слоя во много раз меньше радиуса Земли, будем считать выполненным неравенство
Используя малость параметра
Подставляя выражение (3.8) для величины β в соотношение (2.28), при
Найдем частное решение неоднородного уравнения (2.11) в сферических координатах. В предположении азимутальной симметрии s w:val="28"/></w:rPr><m:t>в?‚П†</m:t></m:r></m:den></m:f><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>=0</m:t></m:r></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> g w:val="EN-US"/></w:rPr><m:t>ОІ</m:t></m:r></m:den></m:f><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>,</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
Исключая из третьего уравнения (3.11) меридиальную компоненту скорости
Учитывая в уравнении (3.12) выражение (3.8) для
Частное решение неоднородного уравнения (3.13) разыскиваем в виде
В результате для функции
Частное решение неоднородного уравнения (3.15) имеет вид
В результате на основе соотношений (3.11), (3.14) и (3.16) получаем следующие выражения для компонент скорости в частном решении неоднородного уравнения (2.11)
Заключение. Данная курсовая работа посвящена анализу винтовых потов в атмосфере Земли. Основной целью моей работы является изучение винтовых потоков в атмосфере Земли. Поставленные мною задачи: · рассмотреть винтовые потоки (течения Бельтрами); · изучить исходные уравнения; · рассмотреть уравнения для винтовых течений в декартовых, круговых цилиндрических и сферических координатах; · рассмотреть винтовые течения в сферических координатах при наличии осевой симметрии; · изучить поверхности тока вихрей первой и второй степени; · изучить винтовые потоки с винтовой симметрией поля течения; были полностью достигнуты при ее написании. Список используемой литературы. КУРСОВАЯ РАБОТА по дисциплине «Геофизическая гидродинамика» на тему: «Анализ винтовых потоков в атмосфере Земли»
Выполнил: Кравцова А.С. студент 4 курса группы «ФИЗ-б-о-111» направления (специальности) Физика очной формы обучения ________________________ (подпись)
Руководитель работы: Шевченко А. И. доцент кафедры теоретической физики
Работа допущена к защите _______________________ ______________ (подпись руководителя) (дата)
Работа выполнена и защищена с оценкой _________________________ Дата защиты______________
Члены комиссии: зав.каф. тер.физики __________ Волкова В.И. доцент каф. тер.физики __________ Шевченко А.И. доцент каф. тер.физики __________ Смерек Ю.Л. доцент каф. тер.физики __________ Кульгина Л.М.
Ставрополь, 2014 г. Содержание Содержание………………………………………………………………………..2 Введение…………………………………………………………………………...3 1. Винтовые потоки (течения Бельтрами)……………………………………….4 1.1. Двумерные течения………………………………………………………..6 1.2. Одномерные течения…………………………………………………...…7 2. Исходные уравнения………………………………………………………….10 3. Уравнения для винтовых течений в декартовых, круговых цилиндрических и сферических координатах……………………………………………………..15 3.1. Декартовы и круговые цилиндрические координаты…………………15 3.2. Сферические координаты……………………………………………….17 4. Винтовые течения в сферических координатах при наличии осевой симметрии………………………………………………………………………..20 5. Поверхности тока вихрей первой и второй степени………………………..24 6. Винтовые потоки с винтовой симметрией поля течения…………………..27 Заключение……………………………………………………………………….29 Список используемой литературы……………………………………………...30
Введение. Основы теории винтовых потоков были заложены в 1881 г. И.С. Громекой в его малоизвестной диссертации "Некоторые случаи движения несжимаемой жидкости" и независимо в 1889 г. в более известной работе итальянского математика Бельтрами (по этой причине винтовые потоки известны еще как течения Бельтрами). Цель: Изучить винтовые потоки в атмосфере Земли. Задачи: · Рассмотреть винтовые потоки (течения Бельтрами); · Изучить исходные уравнения; · Рассмотреть уравнения для винтовых течений в декартовых, круговых цилиндрических и сферических координатах; · Рассмотреть винтовые течения в сферических координатах при наличии осевой симметрии; · Изучить поверхности тока вихрей первой и второй степени; · Изучить винтовые потоки с винтовой симметрией поля течения. · Винтовые потоки (течения Бельтрами). Винтовое движение является важным частным случаем завихренного установившегося движения идеальной жидкости, когда вихревые линии совпадают с линиями тока (кинематическое условие). Эквивалентное энергетическое условие заключается в том, что механическая энергия постоянна во всей массе движущейся жидкости, т.е. теорема Бернулли справедлива для всего потока в целом. В общем случае стационарного вихревого движения невязкой жидкости частицы, движущиеся по разным линиям тока, обладают неодинаковым количеством энергии, т.е. постоянная Бернулли имеет различные значения на разных линиях тока. Вместе с тем вдоль каждой линии тока количество энергии остается одинаковым, т.е. константа Бернулли сохраняется. Если все линии тока будут начинаться в области, где жидкость покоится или движется поступательно с одинаковыми скоростями, то и во всем остальном пространстве вследствие сохранения константы Бернулли вдоль линий тока количество энергии всех частиц будет одинаковым, т.е. поток будет либо потенциальным, либо винтовым. Важными примерами таких движений может стать образование закрученного течения при истечении струи из сосуда с покоящейся жидкостью или возникновение за изгибами русел и после поворотов в трубах циркуляционного движения в изначально равномерном потоке. Однако при применении модели винтовых течений даже в таких очевидных примерах следует помнить о том, что эти рассуждения справедливы только в рамках установившихся движений идеальной жидкости и остаются в силе только при таких режимах течений, где вязкость жидкости и нестационарность движения играют незначительную роль. Кинематическое условие винтового движения может быть выражено следующим образом:
причем в общем случае
Если воспользовавшись соотношениями
Найдем скорости. Одно интересное свойство винтового потока сжимаемой невязкой жидкости следует из уравнения (1.1), если к его обеим частям применить операцию
Подставив сюда выражение для
Это означает, что вдоль линии тока отношение Для однородного винтового потока с соленоидальным полем скорости
В самом деле, это соотношение следует из (1.1) после применения операции ротора к правой и левой частям. Причем из того, что в этом случае
Не следует, что однородный винтовой поток возможен только для несжимаемой жидкости. Из уравнения неразрывности следует, что для сжимаемого газа установившийся однородный винтовой поток возможен, если Уравнения неоднородного винтового потока (1.1) в криволинейных ортогональных координатах запишутся так:
Уравнения (1.2) совместно с уравнением неразрывности для случая установившегося винтового движения сжимаемой жидкости дают нам систему четырех уравнений для определения четырех неизвестных Таким образом, поле скорости для винтовых движений по аналогии с потенциальными течениями полностью определяется из кинематических уравнений, а законы динамики в виде интеграла Бернулли применяются для восстановления поля давления.
Двумерные течения. В общем случае в каждый момент времени поле скоростей потока жидкости определяется тремя функциями -
Поток, который может быть отнесен к такой координатной системе, что-бы все три компоненты скорости -
будем называть двумерным. Геометрически это означает, что на всех координатных поверхностях
Отсюда вытекает, что якобиан от составляющих скорости по координатам тождественно равен нулю
Следовательно, между функциями
которая позволяет одновременно с уменьшением числа переменных в уравнениях движения сократить число уравнений в системе. Одномерные течения. По аналогии с двумерными течениями одномерными потоками назовем течения, которые могут быть отнесены к такой координатной системе, в которой компоненты скорости будут функциями одной координаты
Очевидно, что все рассмотренные примеры двумерных течений в предположении (1.4) могут быть существенно упрощены. Из всего множества возможных случаев перехода от двумерных потоков к одномерным ограничимся рассмотрением двух важных примеров с постоянным распределением завихренности.
1. Пусть скорость плоскопараллельного установившегося течения в инерциальной системе координат имеет только одну составляющую
Отсюда
Это течение изображено на рис. 1.8 и называется сдвиговым течением. В частном случае (
2. Пусть имеется установившееся течение с постоянной величиной завихренности, которое в цилиндрической системе координат имеет только одну окружную составляющую
После интегрирования находим
Для течений с ограниченными скоростями константу Исходные уравнения. Система уравнений идеального изотермического газа применительно к атмосфере Земли в пренебрежении центробежной силой имеет следующий вид:
где Пусть течения однородные винтовые:
Здесь
Решая уравнение (5) относительно плотности, запишем
Как известно, для стандартной атмосферы в ее 70 - километровом (по толщине) слое абсолютная температура отличается от ее среднего значения не более, чем на 5 %</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
Следовательно, в выражении (2.6) множитель, включающий скорость, весьма мало отличается от единицы. В результате с погрешностью, не превышающей
Полагая, найдем. В результате будем иметь
С
|
||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 383; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.82.108 (0.009 с.) |

 - компонентами вектора скорости в некоторой криволинейной системе координат
- компонентами вектора скорости в некоторой криволинейной системе координат  .
.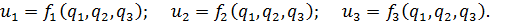
 - и не зависели от третьей —
- и не зависели от третьей —  , т.е.
, т.е.
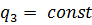 поле скоростей строится одинаковым образом. Иначе говоря,
поле скоростей строится одинаковым образом. Иначе говоря,


 ,
,
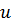 вдоль оси
вдоль оси  и она будет функцией только одной координаты
и она будет функцией только одной координаты  . Тогда имеем
. Тогда имеем
 , где
, где 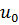 - скорость на оси
- скорость на оси  . Следовательно, рассматриваемое течение обладает скоростью, которая по линейному закону меняется вдоль оси
. Следовательно, рассматриваемое течение обладает скоростью, которая по линейному закону меняется вдоль оси  . Функция тока такого течения имеет вид
. Функция тока такого течения имеет вид
 ) все частицы жидкости движутся с одинаковыми постоянными скоростями
) все частицы жидкости движутся с одинаковыми постоянными скоростями 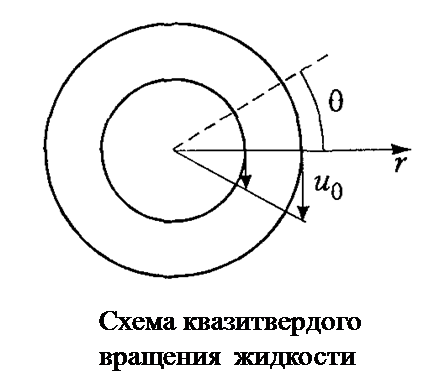

 . Записав в цилиндрической системе координат, с учетом сделанных предположений получим
. Записав в цилиндрической системе координат, с учетом сделанных предположений получим

 следует положить равной нулю. Линиями тока такого течения являются концентрические окружности (на схеме квазитвердого вращения жидкости), а окружная скорость меняется по линейному закону вдоль радиуса. Такое течение обычно называют квазитвердым вращением.
следует положить равной нулю. Линиями тока такого течения являются концентрические окружности (на схеме квазитвердого вращения жидкости), а окружная скорость меняется по линейному закону вдоль радиуса. Такое течение обычно называют квазитвердым вращением. 



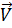 - скорость;
- скорость; 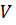 – ее модуль;
– ее модуль;  – давление;
– давление;  - плотность;
- плотность;  - плотность атмосферы у Земли;
- плотность атмосферы у Земли;  - единичный вектор вдоль оси вращения. Рассмотрение проводится в ортогональной системе координат
- единичный вектор вдоль оси вращения. Рассмотрение проводится в ортогональной системе координат  .
.
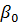 – параметр спиральности. Отметим, что уравнение неразрывности (2.2) является следствием уравнения (2.4). Действительно, применяя к левой и правой частям соотношения (2.4) операцию дивергенции, приходим к уравнению (2.2). С учетом уравнения (2.4) из уравнения движения (2.1) следует
– параметр спиральности. Отметим, что уравнение неразрывности (2.2) является следствием уравнения (2.4). Действительно, применяя к левой и правой частям соотношения (2.4) операцию дивергенции, приходим к уравнению (2.2). С учетом уравнения (2.4) из уравнения движения (2.1) следует

 . Далее примем для температуры
. Далее примем для температуры  , входящей в вышеприведенные соотношения, среднее значение температуры стандартной атмосферы по указанному слою,
, входящей в вышеприведенные соотношения, среднее значение температуры стандартной атмосферы по указанному слою,  Наибольшие скорости, отмеченные в сильных циклонах, не превышают
Наибольшие скорости, отмеченные в сильных циклонах, не превышают  Поэтому выполнено неравенство
Поэтому выполнено неравенство
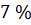 даже при
даже при 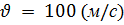 , запишем
, запишем




 – частное решение неоднородного уравнения (2.11). Подставляя (2.12) в уравнение (2.11), приходим к однородному уравнению для определения величины
– частное решение неоднородного уравнения (2.11). Подставляя (2.12) в уравнение (2.11), приходим к однородному уравнению для определения величины 

 коэффициенты Ламе которой удовлетворяют условиям:
коэффициенты Ламе которой удовлетворяют условиям:
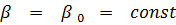 ) был введен следующий обобщенный потенциал S:
) был введен следующий обобщенный потенциал S:


 – оператор Лапласа;
– оператор Лапласа;  – орт, касательный координатной линии
– орт, касательный координатной линии 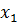 ;
;  – заданная функция своего аргумента, выбираемая из соображения удобства. При этом рассмотрение также проводилось в ортогональной системе координат, коэффициенты Ламе которой удовлетворяют условиям (2.14).
– заданная функция своего аргумента, выбираемая из соображения удобства. При этом рассмотрение также проводилось в ортогональной системе координат, коэффициенты Ламе которой удовлетворяют условиям (2.14).

 – обобщенный потенциал; величины
– обобщенный потенциал; величины  – пока произвольные функции своего аргумента. Подставим выражение (2.16) для величины
– пока произвольные функции своего аргумента. Подставим выражение (2.16) для величины  в уравнение (213). В результате запишем:
в уравнение (213). В результате запишем:

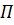 и (
и ( ) под знаком градиента, коэффициент при
) под знаком градиента, коэффициент при 







 следующим образом:
следующим образом:
 играет ту же роль, что и в соотношениях (2.15). В результате придeм к следующему уравнению:
играет ту же роль, что и в соотношениях (2.15). В результате придeм к следующему уравнению:

 , три цилиндрических (круговая, эллиптическая и параболическая;
, три цилиндрических (круговая, эллиптическая и параболическая;  ), а также сферическая и коническая системы
), а также сферическая и коническая системы 
 . В результате уравнение (2.27) принимает вид:
. В результате уравнение (2.27) принимает вид:
 – оператор Лапласа. В случае сферической и конической систем координат удобно положить
– оператор Лапласа. В случае сферической и конической систем координат удобно положить  . В результате уравнение (2.27) принимает вид:
. В результате уравнение (2.27) принимает вид:
 рассмотрим потенциальные течения
рассмотрим потенциальные течения

 Это предположение является приближенным. Oтметим, что модели неизотермической атмосферы рассматривались в cравнительно недавней работе.
Это предположение является приближенным. Oтметим, что модели неизотермической атмосферы рассматривались в cравнительно недавней работе. для плотности ρ справедливо выражение
для плотности ρ справедливо выражение
 радиус Земли, величина α0 определяется согласно выражения (3.1). Принимая естественное допущение, из (2.11) и (3.7) приближенно получаем
радиус Земли, величина α0 определяется согласно выражения (3.1). Принимая естественное допущение, из (2.11) и (3.7) приближенно получаем

 , можем пренебречь соответствующими слагаемыми в уравнении (2.30). Переходя затем в получившемся уравнении от независимых переменных
, можем пренебречь соответствующими слагаемыми в уравнении (2.30). Переходя затем в получившемся уравнении от независимых переменных  и используя также малость параметра
и используя также малость параметра  , приходим к следующему уравнению:
, приходим к следующему уравнению:

 с учетом малости параметров
с учетом малости параметров  и
и  получаем
получаем

 с учетом малости параметров
с учетом малости параметров 


 с помощью второго уравнения, получаем следующее уравнение для определения азимутальной компоненты:
с помощью второго уравнения, получаем следующее уравнение для определения азимутальной компоненты:
 ,находим
,находим

 из запишем уравнение
из запишем уравнение





 . может быть произвольной функцией координат
. может быть произвольной функцией координат
 , то винтовой поток называют однородным, в противном случае - неоднородным. Умножив обе части уравнения (1.1) скалярно на и
, то винтовой поток называют однородным, в противном случае - неоднородным. Умножив обе части уравнения (1.1) скалярно на и 
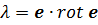 , где
, где  - единичный вектор, коллинеарный вектору
- единичный вектор, коллинеарный вектору . Тогда получим
. Тогда получим , так как
, так как  .
. из уравнения неразрывности, найдем
из уравнения неразрывности, найдем
 . Для несжимаемой жидкости отсюда как частный случай вытекает результат: линии тока располагаются на поверхностях
. Для несжимаемой жидкости отсюда как частный случай вытекает результат: линии тока располагаются на поверхностях  .
. И.С. Громека получил, что вектор скорости и должен удовлетворять векторному уравнению
И.С. Громека получил, что вектор скорости и должен удовлетворять векторному уравнению
 ,
, , т. е. вектор скорости ортогонален градиенту плотности - линии тока располагаются на поверхностях равной плотности.
, т. е. вектор скорости ортогонален градиенту плотности - линии тока располагаются на поверхностях равной плотности.
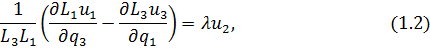
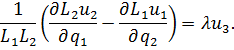
 .
.


