
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения для винтовых течений в декартовых, круговых цилиндрических и сферических координатах.Содержание книги
Поиск на нашем сайте
Декартовы и круговые цилиндрические координаты. Пусть система координат декартова
Здесь t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>S=0,</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
Подставляя выражение (3.1) для
Приведем частные решения
где
В частном решении неоднородного уравнения (2.11) в круговых цилиндрических координатах
Здесь компоненты скорости Элементарное решение уравнения (3.3) в декартовых координатах, получаемое методом разделения переменных, имеет вид
Здесь и далее
Здесь и далее Аналогичным образом в декартовых и круговых цилиндрических координатах можно получить элементарное решение уравнения (2.32) для потенциала
Здесь
Сферические координаты. В сферических координатах
Здесь
Учитывая, что толщина атмосферного слоя во много раз меньше радиуса Земли, будем считать выполненным неравенство
Используя малость параметра
Подставляя выражение (3.8) для величины β в соотношение (2.28), при
Найдем частное решение неоднородного уравнения (2.11) в сферических координатах. В предположении азимутальной симметрии s w:val="28"/></w:rPr><m:t>в?‚П†</m:t></m:r></m:den></m:f><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>=0</m:t></m:r></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> g w:val="EN-US"/></w:rPr><m:t>ОІ</m:t></m:r></m:den></m:f><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>,</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
Исключая из третьего уравнения (3.11) меридиальную компоненту скорости
Учитывая в уравнении (3.12) выражение (3.8) для
Частное решение неоднородного уравнения (3.13) разыскиваем в виде
В результате для функции
Частное решение неоднородного уравнения (3.15) имеет вид
В результате на основе соотношений (3.11), (3.14) и (3.16) получаем следующие выражения для компонент скорости в частном решении неоднородного уравнения (2.11)
|
||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 195; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.96.19 (0.01 с.) |

 или круговая цилиндрическая
или круговая цилиндрическая  причем ось s w:val="28"/></w:rPr><m:t>в‰Ў</m:t></m:r><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>z</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
причем ось s w:val="28"/></w:rPr><m:t>в‰Ў</m:t></m:r><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>z</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  направлена против вектора силы тяжести. Тогда выражения (2.9) для плотности и (2.11) для величины
направлена против вектора силы тяжести. Тогда выражения (2.9) для плотности и (2.11) для величины  принимают вид
принимают вид

 – ускорение силы тяжести. Подставляя выражение (2.1) для
– ускорение силы тяжести. Подставляя выражение (2.1) для 


 , при
, при  , соответственно в декартовой и круговой цилиндрической системах координат получаем:
, соответственно в декартовой и круговой цилиндрической системах координат получаем:


 неоднородного уравнения (2.11) в случаях декартовой и круговой цилиндрической систем координат. Для единичного вектора
неоднородного уравнения (2.11) в случаях декартовой и круговой цилиндрической систем координат. Для единичного вектора  примем выражение
примем выражение
 – меридиональный угол начала системы отсчета. В результате в декартовых координатах
– меридиональный угол начала системы отсчета. В результате в декартовых координатах 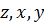 это решение запишется в виде
это решение запишется в виде


 выражение для компоненты скорости
выражение для компоненты скорости  имеет вид (3.5). Выражения для компонент скорости
имеет вид (3.5). Выражения для компонент скорости  имеют следующий вид:
имеют следующий вид:

 определяются выражениями (3.5).
определяются выражениями (3.5).
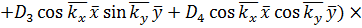



 – постоянная разделения;
– постоянная разделения;  постоянные;
постоянные;  – функция Бесселя. Элементарное решение в круговых цилиндрических координатах таково
– функция Бесселя. Элементарное решение в круговых цилиндрических координатах таково


 – постоянные;
– постоянные;  – функции Бесселя и Неймана.
– функции Бесселя и Неймана. . В частности, в круговых цилиндрических координатах оно имеет вид
. В частности, в круговых цилиндрических координатах оно имеет вид

 и
и  - постоянные.
- постоянные. для плотности ρ справедливо выражение
для плотности ρ справедливо выражение
 радиус Земли, величина α0 определяется согласно выражения (3.1). Принимая естественное допущение, из (2.11) и (3.7) приближенно получаем
радиус Земли, величина α0 определяется согласно выражения (3.1). Принимая естественное допущение, из (2.11) и (3.7) приближенно получаем

 , можем пренебречь соответствующими слагаемыми в уравнении (2.30). Переходя затем в получившемся уравнении от независимых переменных
, можем пренебречь соответствующими слагаемыми в уравнении (2.30). Переходя затем в получившемся уравнении от независимых переменных  и используя также малость параметра
и используя также малость параметра  , приходим к следующему уравнению:
, приходим к следующему уравнению:

 с учетом малости параметров
с учетом малости параметров  и
и  получаем
получаем

 с учетом малости параметров
с учетом малости параметров 


 с помощью второго уравнения, получаем следующее уравнение для определения азимутальной компоненты:
с помощью второго уравнения, получаем следующее уравнение для определения азимутальной компоненты:


 из запишем уравнение
из запишем уравнение







