
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Винтовые течения в сферических координатах при наличии осевой симметрии.Содержание книги
Поиск на нашем сайте Обратимся к системе уравнений (2.10) и (2.11) в сферических координатах
Полагая наличие осевой симметрии s w:val="28"/></w:rPr><m:t>в?‚П†</m:t></m:r></m:den></m:f><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>=0</m:t></m:r></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
Здесь
Учитывая в
Положим во втором слагаемом левой части и в правой части уравнения (4.4) приближенно
Частное решение неоднородного уравнения (4.5) разыскиваем в виде
Учитывая выражение (4.6) в уравнении (4.5), запишем
Анализ показал, что вторым слагаемым в левой части уравнения можно пренебречь. В результате для величины
Соответствующие (4.8) величины компонент скорости таковы:
Получим общее решение однородного (
При этом было приближенно положено
Записываем элементарное решение уравнения (4.11) с помощью метода разделения переменных
Подставляя выражение (4.12) в уравнение (4.11), для величин
Здесь
Они представляют собой полиномы Лежандра n-й степени первого порядка:
Решения уравнения (4.13) при выполнении условий (4.15) выражаются через функции Бесселя:
Таким образом, ограниченное и обладающее непрерывными до второго порядка производными на сфере решение уравнения (4.11), получаемое методом разделения переменных, запишем в виде
С учетом соотношений (4.8), (4.10) и (4.18) для функции тока имеем
В заключение данного параграфа отметим, что ограниченное и обладающее непрерывными до второго порядка производными на сфере решение уравнения (3.41), получаемое методом разделения переменных, имеет следующий вид:
Здесь
Поверхности тока вихрей первой и второй степени. В пренебрежении эффектом вращения (
Соответственно для компонент скорости имеем
Пусть имеют место условия
Здесь при
Условие нетривиальной разрешимости системы уравнений (5.4) имеет вид
Его решение таково:
Решая первое уравнение (5.4) относительно
При
Рассматривая при
Соответствующие поверхности тока при
|
||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 268; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 . Полагая ось вращения параллельной оси
. Полагая ось вращения параллельной оси  , для вектора
, для вектора  запишем
запишем
 ,решаем уравнение неразрывности (2.10):
,решаем уравнение неразрывности (2.10):

 – функция тока. Интегрируя
– функция тока. Интегрируя  - и
- и  - компоненты уравнения (2.11), выражаем -компоненту скорости через функцию тока:
- компоненты уравнения (2.11), выражаем -компоненту скорости через функцию тока:
 – компоненте уравнения (2.11) выражения (4.2) и (4.3), получаем следующее уравнение для функции тока
– компоненте уравнения (2.11) выражения (4.2) и (4.3), получаем следующее уравнение для функции тока 

 . Переходя, далее, от дифференцирования по
. Переходя, далее, от дифференцирования по 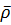 , приходим к следующему уравнению:
, приходим к следующему уравнению:




 получаем следующее выражение:
получаем следующее выражение:

 ) уравнения (4.5). Для этого удобно выразить функцию тока
) уравнения (4.5). Для этого удобно выразить функцию тока 



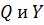 соответственно получаем уравнения
соответственно получаем уравнения

 – постоянная разделения. Ограниченные и обладающие непрерывными до второго порядка производными решения уравнения (4.14) существуют лишь при
– постоянная разделения. Ограниченные и обладающие непрерывными до второго порядка производными решения уравнения (4.14) существуют лишь при






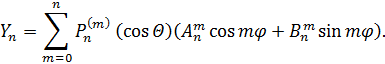
 – сферические функции; величины
– сферические функции; величины  определяются согласно соотношений (3.17).
определяются согласно соотношений (3.17).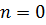 ) слагаемое в соотношении (3.19). Согласно (3.17), имеем
) слагаемое в соотношении (3.19). Согласно (3.17), имеем 
 . Таким образом, с большой точностью можно положить
. Таким образом, с большой точностью можно положить  . В результате, переобозначая постоянные
. В результате, переобозначая постоянные  , запишем
, запишем




 принято условие “твердой крышки”, как это иногда делается в динамике атмосферы. Подставляя выражение (5.2) для
принято условие “твердой крышки”, как это иногда делается в динамике атмосферы. Подставляя выражение (5.2) для  в условия (5.3), имеем
в условия (5.3), имеем



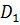 , исключаем затем коэффициент
, исключаем затем коэффициент 
 соотношение (5.7) определяет поверхности тока
соотношение (5.7) определяет поверхности тока  в вихре первой степени. Для
в вихре первой степени. Для  и высоты “твердой крышки”
и высоты “твердой крышки”
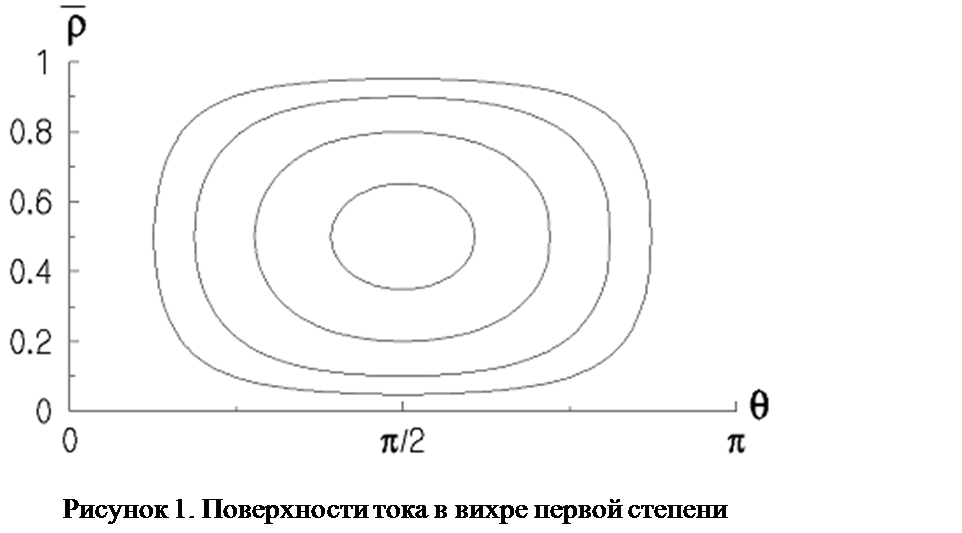 Эти поверхности представлены на рисунке 1.
Эти поверхности представлены на рисунке 1. ) слагаемое в соотношении (4.19), для функции тока вихря второй степени аналогично случаю вихря первой степени получаем
) слагаемое в соотношении (4.19), для функции тока вихря второй степени аналогично случаю вихря первой степени получаем
 представлены на рисунке 2. Как видно из рисунка 1 и 2, вихрь первой степени содержит одну циркуляционную зону, вихрь второй степени – две. Можно показать, что вихрь третьей (
представлены на рисунке 2. Как видно из рисунка 1 и 2, вихрь первой степени содержит одну циркуляционную зону, вихрь второй степени – две. Можно показать, что вихрь третьей ( ) степени содержит три циркуляционные зоны и т. д.
) степени содержит три циркуляционные зоны и т. д.



