
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерференция двух монохроматических волнСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте В идеальном случае монохроматических источников при наложении двух пучков света с интенсивностями
где
Интерференция волн от двух точечных монохроматических источников. Характер наблюдаемой интерференционной картины зависит от взаимного расположения источников Каждый интерференционный максимум (светлая полоса) соответствует разности хода
При симметричном расположении экрана по отношению к лучам 1 и 2 ширина интерференционных полос выражается соотношением: Приближение Одной из важных характеристик наблюдаемой интерференционной картины является видность V, которая характеризует контраст интерференционных полос. По определению
где При интерференции монохроматических волн видность V зависит только от соотношения интенсивностей интерферирующих пучков света и выражается формулой:
В случае пучков равной интенсивности (
При этом видность интерференционной картины максимальна и равна единице. При Основные понятия в теории интерференции. Оптическая длина пути и оптическая разность хода. Условия максимумов и минимумов интенсивности света через разность фаз и оптическую разность хода. (см. также вопрос 27) Оптическая длина пути, оптический путь, между точками А и В прозрачной среды; расстояние, на которое свет (оптическое излучение) распространился бы в вакууме за время его прохождения от А до В. Поскольку скорость света в любой среде меньше его скорости в вакууме, О. д. п. всегда больше реально проходимого светом расстояния (или, в предельном случае вакуума, равна ему). В оптической системе, состоящей из р однородных сред (траектория луча света в такой системе — ломаная линия), О. д. п. равна
Разность хода лучей, разность оптических длин путей двух световых лучей, имеющих общие начальную и конечную точки. Понятие Р. х. играет основную роль в описании интерференции света и дифракции света. Расчёты распределения световой энергии в оптических системах основаны на вычислении Р. х. проходящих через них лучей (или пучков лучей). Оптическая разность хода. Вместо разности фаз
Изменению разности фаз на В вакууме оптическая разность хода в отличие от разности фаз имеет наглядную интерпретацию. Если две интерферирующие волны испускаются одним источником света, то разность хода - это геометрическая разность длин путей, по которым два интерферирующих луча от одной точки источника достигли одной точки экрана.
Например, в оптической схеме опыта Юнга, изображенной на рис. 18, разность хода для точки P на экране находится по формуле: . В изотропной среде скорость света в n раз меньше, чем в вакууме, здесь n - показатель преломления среды. Частота света в среде и в вакууме одинакова, поэтому длина волны в среде в n раз меньше. В соответствии с соотношением Заменяя разность фаз интерферирующих волн оптической разностью хода, получаем следующее выражение для интенсивности интерференционной картины: . Приемники света в оптическом диапазоне реагируют на интенсивность света, а не на напряженность электрического или магнитного полей. Поэтому измеряемые в опыте величины, ширина полос и видность, также могут быть выражены через интенсивность, а значит и через оптическую разность хода. Следовательно, понятие оптической разности хода позволяет свести оптическую задачу по интерференции к геометрической задаче отыскания разности хода. Отметим, что разность хода лучей можно отсчитывать не только как разность длин путей от источника до точки наблюдения, но и как разность длин путей от двух точек любой поверхности равной фазы волны до точки наблюдения. При этом, конечно, две точки на поверхности равной фазы - не произвольные точки, а должны быть точками, через которые реально проходят лучи, попадающие в точку наблюдения. Так на рис. 18 18.1.2.1. Условия максимума и минимума на разность фаз δ
Оптическая разность хода Пусть для простоты, начальные фазы α1 и α2 интерферирующих волн равны нулю, тогда:
здесь λ0 = cT - длина световой волны в вакууме. Оптической разностью хода называют величину:
Тогда:
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1444; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |

 и
и 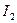 распределение интенсивности в интерференционной картине описывается формулой:
распределение интенсивности в интерференционной картине описывается формулой: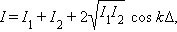
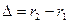 – разность хода интерферирующих волн,
– разность хода интерферирующих волн, 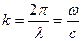 – волновое число.
– волновое число.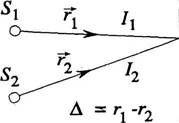 Рисунок 1.1.
Рисунок 1.1. и
и  и плоскости наблюдения P (рис. 1.1). Интерференционные полосы могут иметь, например, вид семейства концентрических колец или гипербол. Наиболее простой вид имеет интерференционная картина, полученная при наложении двух плоских монохроматических волн, когда источники
и плоскости наблюдения P (рис. 1.1). Интерференционные полосы могут иметь, например, вид семейства концентрических колец или гипербол. Наиболее простой вид имеет интерференционная картина, полученная при наложении двух плоских монохроматических волн, когда источники 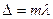 , где m – целое число, которое называется порядком интерференции. В частности, при
, где m – целое число, которое называется порядком интерференции. В частности, при 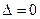 возникает интерференционный максимум нулевого порядка. В случае интерференции двух плоских волн ширина интерференционных полос l простым соотношением связана с углом схождения интерферерирующих лучей на экране (рис. ниже).
возникает интерференционный максимум нулевого порядка. В случае интерференции двух плоских волн ширина интерференционных полос l простым соотношением связана с углом схождения интерферерирующих лучей на экране (рис. ниже).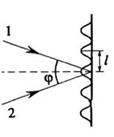
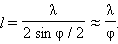
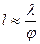 , справедливое при малых углах
, справедливое при малых углах  , применимо ко многим оптическим интерференционным схемам.
, применимо ко многим оптическим интерференционным схемам.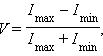
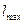 и
и 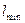 – соответственно максимальное и минимальное значения интенсивности в интерференционной картине.
– соответственно максимальное и минимальное значения интенсивности в интерференционной картине.
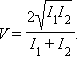
 ) из (1.1) следует:
) из (1.1) следует: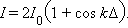
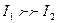 видность картины стремится к нулю и
видность картины стремится к нулю и  , где lk — расстояние, пройденное светом в k -той среде (k = 1, 2,..., р), nk — показатель преломления этой среды, å — знак суммы. Для одной среды (р = 1) сумма сокращается до единственного члена ln . В оптически неоднородной среде (с плавно меняющимся n; траектория луча в такой среде — кривая линия), О. д. п. есть
, где lk — расстояние, пройденное светом в k -той среде (k = 1, 2,..., р), nk — показатель преломления этой среды, å — знак суммы. Для одной среды (р = 1) сумма сокращается до единственного члена ln . В оптически неоднородной среде (с плавно меняющимся n; траектория луча в такой среде — кривая линия), О. д. п. есть  , где dl — бесконечно малый элемент траектории луча. Понятие О. д. п. играет большую роль в оптике, особенно в геометрической оптике и кристаллооптике, позволяя сопоставлять пути, проходимые светом в средах, в которых скорость его распространения различна. Геометрическое место точек, для которых О. д. п., отсчитываемая от одного источника, одинакова, называется поверхностью световой волны; световые колебания на этой поверхности находятся в одинаковой фазе.
, где dl — бесконечно малый элемент траектории луча. Понятие О. д. п. играет большую роль в оптике, особенно в геометрической оптике и кристаллооптике, позволяя сопоставлять пути, проходимые светом в средах, в которых скорость его распространения различна. Геометрическое место точек, для которых О. д. п., отсчитываемая от одного источника, одинакова, называется поверхностью световой волны; световые колебания на этой поверхности находятся в одинаковой фазе. интерферирующих волн удобно ввести в рассмотрение пропорциональную ей величину
интерферирующих волн удобно ввести в рассмотрение пропорциональную ей величину  - оптическую разность хода, которая отличается множителем
- оптическую разность хода, которая отличается множителем 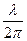 , где
, где 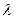 - длина световой волны.
- длина световой волны. 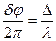
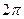 соответствует изменение разности хода на
соответствует изменение разности хода на 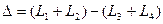

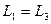 , поэтому две щели находятся на поверхности равной фазы, и, следовательно, разность хода можно найти по упрощенной формуле
, поэтому две щели находятся на поверхности равной фазы, и, следовательно, разность хода можно найти по упрощенной формуле  . Этот прием часто используется при решении задач.
. Этот прием часто используется при решении задач.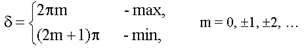
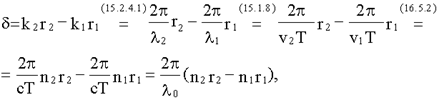
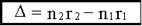 .
. .
.


