
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Явление электростатической индукции, распределение зарядов.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Явление поляризации электростатическим полем макроскопических тел называется электростатической индукцией. При электростатической индукции на одной стороне поверхности тела образуются положительные заряды, на другой стороне отрицательные.
Напряженность поля вблизи проводника перпендикулярна ему, а внутри равна нулю. Электроемкость уединенного проводника. Пример вычисления емкости шарового проводника. Конденсаторы. Емкость конденсатора. Вычисление емкости плоского конденсатора, сферического конденсатора. Все точки проводника в электрическом поле имеют одинаковый потенциал, зависящий от заряда проводника. Чтобы определять потенциал, зная заряд, и наоборот, вводится физическая величина - электрическая ёмкость. Потенциал любого проводника пропорционален его заряду, поэтому их отношение от заряда не зависит и может быть принято за характеристику проводника. Электрической ёмкостью проводника называется отношение заряда проводника к его потенциалу. Проводник называют уединённым, если он находится далеко от других тел, то есть его размеры много меньше расстояний до других тел. Электроёмкость уединённого проводника не зависит от его заряда. Электроёмкость любого проводника не зависит от материала. Она зависит только от формы и размеров проводника. Хотя электроёмкость и определяется через заряд и потенциал, она не зависит ни от заряда, ни от потенциала. Эта величина постоянна для данного уединённого проводника. Практическая польза электроёмкости состоит в том, что, определив её экспериментально или теоритически, можно при известном заряде проводника вычислить его потенциал и наоборот. В действительности проводник никогда не является абсолютно уединённым. Окружающие заряженные тела создают собственные электрические поля, а у незаряженных они возникают в поле проводника (поляризация диэлектриков, проводники в электрическом поле). Поэтому электроёмкость зависит от окружающих тел. Во многих случаях проводник всё же можно считать уединённым. Для некоторых тел электроёмкость вычислить несложно, в частности для уединённого проводящего шара. В СИ единица электроёмкости - фарад (Ф). 1Ф=Кл/В. Ёмкостью в один фарад обладает проводник, потенциал которого увеличивается на один вольт при сообщении заряда один кулон. Фарад - очень большая единица измерения, поэтому, как правило, исползуются производные единицы: микрофарад, 1 мкФ=10-6Ф, и пикофарад, 1 пФ=10-12Ф. Ёмкость земного шара меньше одной тысячной фарада, она равна 709 мкФ. Ёмкостью в один фарад обладал бы шар с радиусом в 13 раз большим радиуса Солнца. Конденсатор - система проводников, электрическая ёмкость которой не зависит от окружающих тел. Он представляет собой два проводника, разделённые слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Эти проводники называют обкладками конденсатора. Электроёмкость конденсатора может быть достаточно велика. Конденсатор также является устройством для накопления электрического заряда.
Чтобы сообщить конденсатору заряд, его нужно зарядить, например, подключив к источнику постоянного (!) тока. Зарядом конденсатора называют модуль заряда любой из его обкладок. Разность потенциалов между обкладками конденсатора пропорциональна напряжённости его поля, которая, в свою очередь, пропорциональна заряду. Следовательно, отношение заряда к разности потенциалов не зависит от заряда. Это позволяет ввести понятие электроёмкости конденсатора. Ёмкость конденсатора зависит от его формы, размера, взаимного расположения обкладок и диэлектрической проницаемости разделяющей их среды. Её можно вычислить, зная эти характеристики. Вычислим электроёмкость плоского конденсатора из двух пластин площадью S, находящихся на расстоянии d, в среде с диэлектрической проницаемостью ε. Напряжённость поля между обкладками равна сумме напряжённостей их полей, причём арифметической, так как они параллельны и одинаково направлены.
εS εε0S Вычислим электроёмкость сферического конденсатора, состоящего из двух концентрических сфер радиусами r1 и r2, r1<r2 с зарядами -q (внутренняя) и +q (внешняя). Потенциал заряженной сферы равен потенциалу точечного заряда, помещённого в её центр.
ε r1r2 r1r2
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 685; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.174.8 (0.007 с.) |

 В металлах ионы кристаллической решетки окружены свободными зарядами (электронами проводимости), которые могут перемещаться под действием поля на большие (в микроскопическом смысле) расстояния. Они накапливаются с той стороны металлического тела, куда «входит» вектор напряженности приложенного поля, а та сторона, откуда этот вектор «выходит», оказывается «обедненной электронами», и потому заряжена положительно. Процесс поляризации проводящего тела продолжается до тех пор, пока поле поляризации E ¢¢ (очевидно, направленное против приложенного поля E ¢) полностью не скомпенсирует E ¢ внутри проводника. В этот момент сила, действующая на электроны проводимости F = e E = e (E ¢ + E ¢¢), уменьшается до нуля, и процесс поляризации прекращается. В установившемся режиме
В металлах ионы кристаллической решетки окружены свободными зарядами (электронами проводимости), которые могут перемещаться под действием поля на большие (в микроскопическом смысле) расстояния. Они накапливаются с той стороны металлического тела, куда «входит» вектор напряженности приложенного поля, а та сторона, откуда этот вектор «выходит», оказывается «обедненной электронами», и потому заряжена положительно. Процесс поляризации проводящего тела продолжается до тех пор, пока поле поляризации E ¢¢ (очевидно, направленное против приложенного поля E ¢) полностью не скомпенсирует E ¢ внутри проводника. В этот момент сила, действующая на электроны проводимости F = e E = e (E ¢ + E ¢¢), уменьшается до нуля, и процесс поляризации прекращается. В установившемся режиме 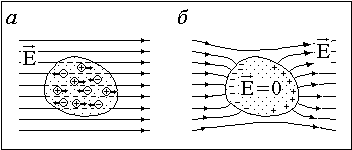 внутри проводника электростатическое поле отсутствует (Е = 0), а также равна нулю объемная плотность заряда. Избыточные заряды сосредоточены на поверхности проводника. На поверхности равна нулю касательная к поверхности компонента Е ( иначеэлектроны продолжали бы перемещаться вдоль поверхности). На рисунке показана картина силовых линий поля вблизи проводника до начала процесса электростатической индукции и в установившемся режиме. Длительность процесса поляризации проводника оценивается в пределах одной микросекунды.
внутри проводника электростатическое поле отсутствует (Е = 0), а также равна нулю объемная плотность заряда. Избыточные заряды сосредоточены на поверхности проводника. На поверхности равна нулю касательная к поверхности компонента Е ( иначеэлектроны продолжали бы перемещаться вдоль поверхности). На рисунке показана картина силовых линий поля вблизи проводника до начала процесса электростатической индукции и в установившемся режиме. Длительность процесса поляризации проводника оценивается в пределах одной микросекунды. Простейший плоский конденсатор состоит из двух противоположно заряженных пластин. Если заряды пластин одинаковы по модулю и противопложны по знаку, поле конденсатора почти полностью сосредоточено между его обкладками. Напряжённость направлена от положительно заряженной пластины к отрицательно заряженной. Поле плоского конденсатора между его обкладками можно считать однородным. Поле сферического конденсатора, состоящего из двух концентрических сфер, полностью сосредоточено между обкладками. В этой области оно подобно полю точечного заряда, помещённого в центр внутренней сферы.
Простейший плоский конденсатор состоит из двух противоположно заряженных пластин. Если заряды пластин одинаковы по модулю и противопложны по знаку, поле конденсатора почти полностью сосредоточено между его обкладками. Напряжённость направлена от положительно заряженной пластины к отрицательно заряженной. Поле плоского конденсатора между его обкладками можно считать однородным. Поле сферического конденсатора, состоящего из двух концентрических сфер, полностью сосредоточено между обкладками. В этой области оно подобно полю точечного заряда, помещённого в центр внутренней сферы.


