
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрическое поле в вакууме. Закон кулона. Закон сохранения заряда. Напряженность электрического поля. Напряженность поля точечного заряда. Принцип суперпозиции. Силовые линии поля.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Электрическое поле в вакууме. Закон Кулона. Закон сохранения заряда. Напряженность электрического поля. Напряженность поля точечного заряда. Принцип суперпозиции. Силовые линии поля. Электрическое поле — особая форма поля, существующая вокруг тел или частиц, обладающих электрическим зарядом, а также в свободном виде в электромагнитных волнах. Электрическое поле непосредственно невидимо, но может наблюдаться по его действию и с помощью приборов. Основным действием электрического поля является ускорение тел или частиц, обладающих электрическим зарядом. Электрическое поле можно рассматривать как математическую модель, описывающую значение величины напряженности электрического поля в данной точке пространства. Электрическое поле является одной из составляющих единого электромагнитного поля и проявлением электромагнитного взаимодействия. В настоящее время наука ещё не достигла понимания физической сущности таких полей, как электрическое, магнитное и гравитационное, а также их взаимодействия друг с другом. Пока еще только описаны результаты их механического воздействия на заряженные тела, а также существует теория электромагнитной волны, описываемая Уравнениями Максвелла. Эффект поля — Эффект поля заключается в том, что при воздействии электрического поля на поверхность электропроводящей среды в её приповерхностном слое изменяется концентрация свободных носителей заряда. Этот эффект лежит в основе работы полевых транзисторов. Основным действием электрического поля является силовое воздействие на неподвижные (относительно наблюдателя) электрически заряженные тела или частицы. Если заряженное тело фиксировано в пространстве, то оно под действием силы не ускоряется. На движущиеся заряды силовое воздействие оказывает и магнитное поле (вторая составляюшая силы Лоренца). Зако́н Куло́на — это закон взаимодействия точечных электрических зарядов. Был открыт Кулоном в 1785 г. Проведя большое количество опытов с металлическими шариками Шарль Кулон дал такую формулировку закона: Поток вектора напряженности электростатического поля. Теорема Гаусса и ее применение к расчету напряженности полей. Поле бесконечной равномерно заряженной плоскости. Поле заряженной сферы и заряженного шара. Поле бесконечной равномерно заряженной нити. Дифференциальная форма теоремы Гаусса. Поток векторного поля - поток Φ векторного поля
при этом векторный элемент площади поверхности определяется как
где Теорема Гаусса Поток вектора напряжённости электрического поля через любую, произвольно выбранную, замкнутую поверхность равен алгебраической сумме заключённых в этой поверхности электрических зарядов, делённой на электрическую постоянная ε0:
Данное выражение представляет собой теорему Гаусса в интегральной форме. В дифференциальной форме теорема Гаусса выражается следующим образом:
где ρ — объёмная плотность заряда
Теорема Гаусса выражает связь между потоком напряженности электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченной этой поверхностью. Физической основой теоремы Гаусса является закон Кулона или, иначе, теорема Гаусса является интегральной формулировкой закона Кулона.
Работа сил электростатического поля при перемещении зарядов. Потенциальный характер электростатического поля. Циркуляция вектора напряженности электростатического поля. Потенциал электростатического поля. Потенциал поля точечного заряда. Связь между напряженностью и потенциалом. Эквипотенциальные поверхности.
Работа электростатического поля (A)
A = Fd=qEd,
A1 = Fd1 cos a, но d1 cos a = d, A1 = qEd A = A1 A1,2,3,1 = A1,2 + A2,3 + A3,1
A1,2,3,1 = qEd1 cos a + Eqh cos 90° + Eqd cos 180° = qEd + 0 + (- qEd) A1,2,3,1 =0 т. е. работа при перемещении заряда между двумя точками в электростатическом поле не зависит от формы траектории, а зависит от положения этих точек. Работа по замкнутой траектории равна нулю. Электростатическое поле, как и гравитационное, потенциальное. Электростатические силы, как и гравитационные, относятся к консервативным (потенциальным) силам. Работа консервативных сил равна изменению потенциальной энергии взятому с противоположным знаком. A = å D Ai = - (W2 - W1) = - D Wп
Потенциальная энергия W заряда q в однородном электростатическом поле напряженностью E на расстоянии d от 0 потенциального уровня Wп = Eqd Потенциальность электростатического поля.
Суммируя (интегрируя) все элементарные работы, находим что и требовалось доказать. Работа определяется только расстояниями от источника до начальной и конечной точки траектории. Такое силовое поле в механике мы называли потенциальным. Из принципа суперпозиции следует потенциальность электростатического поля, созданного любой системой зарядов. Из (1.6.2) и принципа суперпозиции следует также, что работа электростатических сил над зарядом, перемещаемым по замкнутому контуру, равна 0: Таким образом, для любого контура в электростатическом поле циркуляция напряженности – тождественный нуль. В соответствии с утверждением (1.5.6) напряженность электростатического поля (с точностью до знака) может быть истолкована как градиент некоторой функции координат, называемой потенциалом электростатического поля Используя определение напряженности электростатического поля и формулу связи между силой F и потенциальной энергией W, известную из курса механики из (1.6.4) получим, что потенциал поля в данной точке наблюдения численно равен потенциальной энергии пробного заряда q, помещаемого в данную точку, отнесенной к величине этого заряда: Иначе говоря, поле, работа которого при перемещении заряда по любой замкнутой траектории равна нулю, называют потенциальным. Пример потенциального поля — электростатическое поле.
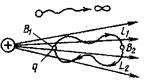
Потенциал В качестве энергетической характеристики поля в данной точке используют потенциал j. Потенциал электростатического поля — отношение потенциальной энергии заряда в поле к этому заряду:
Выражается потенциал в вольтах:
Потенциал j не зависит от заряда q, помещенного в данную точку поля. Для однородного поля
потенциал зависит от напряженности E и от расстояния d от данной точки поля до нулевого потенциального уровня.
Работа поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность характеризует потенциал в данной точке поля созданного точечным зарядом Q смотри рисунок выше,
где Q — заряд создающий поле, R — расстояние от данной точки поля до заряда Q. Потенциальная энергия электрического взаимодействия системы n точечных зарядов qi равна Wп = 1/2åqij i здесь j i — потенциал поля в точке, где находится заряд qi Если поле создано двумя зарядами, то выполняется следствие принципа суперпозиции полей. j = j 1 + j 2 Потенциал поля, созданного несколькими заряженными телами, равен алгебраической сумме потенциалов отдельных полей, создаваемых в данной точке пространства каждым из заряженных тел: j = j 1 + j 2+...+ j n
Проводники в электростатическом поле. Явление электростатической индукции. Свойства индукционных зарядов, характер их распределения. Напряженность поля вблизи поверхности проводника. Поле внутри проводника. Потенциал проводника. Электроемкость уединенного проводника. Пример вычисления емкости шарового проводника. Конденсаторы. Емкость конденсатора. Вычисление емкости плоского конденсатора, сферического конденсатора. Все точки проводника в электрическом поле имеют одинаковый потенциал, зависящий от заряда проводника. Чтобы определять потенциал, зная заряд, и наоборот, вводится физическая величина - электрическая ёмкость. Потенциал любого проводника пропорционален его заряду, поэтому их отношение от заряда не зависит и может быть принято за характеристику проводника. Электрической ёмкостью проводника называется отношение заряда проводника к его потенциалу. Проводник называют уединённым, если он находится далеко от других тел, то есть его размеры много меньше расстояний до других тел. Электроёмкость уединённого проводника не зависит от его заряда. Электроёмкость любого проводника не зависит от материала. Она зависит только от формы и размеров проводника. Хотя электроёмкость и определяется через заряд и потенциал, она не зависит ни от заряда, ни от потенциала. Эта величина постоянна для данного уединённого проводника. Практическая польза электроёмкости состоит в том, что, определив её экспериментально или теоритически, можно при известном заряде проводника вычислить его потенциал и наоборот. В действительности проводник никогда не является абсолютно уединённым. Окружающие заряженные тела создают собственные электрические поля, а у незаряженных они возникают в поле проводника (поляризация диэлектриков, проводники в электрическом поле). Поэтому электроёмкость зависит от окружающих тел. Во многих случаях проводник всё же можно считать уединённым. Для некоторых тел электроёмкость вычислить несложно, в частности для уединённого проводящего шара. В СИ единица электроёмкости - фарад (Ф). 1Ф=Кл/В. Ёмкостью в один фарад обладает проводник, потенциал которого увеличивается на один вольт при сообщении заряда один кулон. Фарад - очень большая единица измерения, поэтому, как правило, исползуются производные единицы: микрофарад, 1 мкФ=10-6Ф, и пикофарад, 1 пФ=10-12Ф. Ёмкость земного шара меньше одной тысячной фарада, она равна 709 мкФ. Ёмкостью в один фарад обладал бы шар с радиусом в 13 раз большим радиуса Солнца. Конденсатор - система проводников, электрическая ёмкость которой не зависит от окружающих тел. Он представляет собой два проводника, разделённые слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Эти проводники называют обкладками конденсатора. Электроёмкость конденсатора может быть достаточно велика. Конденсатор также является устройством для накопления электрического заряда.
Чтобы сообщить конденсатору заряд, его нужно зарядить, например, подключив к источнику постоянного (!) тока. Зарядом конденсатора называют модуль заряда любой из его обкладок. Разность потенциалов между обкладками конденсатора пропорциональна напряжённости его поля, которая, в свою очередь, пропорциональна заряду. Следовательно, отношение заряда к разности потенциалов не зависит от заряда. Это позволяет ввести понятие электроёмкости конденсатора. Ёмкость конденсатора зависит от его формы, размера, взаимного расположения обкладок и диэлектрической проницаемости разделяющей их среды. Её можно вычислить, зная эти характеристики. Вычислим электроёмкость плоского конденсатора из двух пластин площадью S, находящихся на расстоянии d, в среде с диэлектрической проницаемостью ε. Напряжённость поля между обкладками равна сумме напряжённостей их полей, причём арифметической, так как они параллельны и одинаково направлены.
εS εε0S Вычислим электроёмкость сферического конденсатора, состоящего из двух концентрических сфер радиусами r1 и r2, r1<r2 с зарядами -q (внутренняя) и +q (внешняя). Потенциал заряженной сферы равен потенциалу точечного заряда, помещённого в её центр.
ε r1r2 r1r2 Диэлектрики. Полярные и неполярные диэлектрики. Явление поляризации. Вектор поляризации, вектор электрической индукции, связь между ними. Электрическое поле в диэлектриках. Диэлектрическая проницаемость вещества. Теорема Гаусса для вектора индукции (интегральная и дифференциальная формы). Диэлектриками называют вещества, в которых отсутствуют свободные носители зарядов. Тем не менее, как и в любом другом теле, в диэлектрике носители заряда есть, но они не могут смещаться под действием сил электрического поля. Диэлектрики практически не проводят электрический ток - их используют в качестве электрических изоляторов. Удельная электропроводность диэлектриков занимает область, лежащую ниже 10-8 (Ом.м)-1. Mолекула диэлектрика – диполь с дипольным электрическим моментом p = ql, где q – абсолютная величина суммарного положительного (а также суммарного отрицательного) зарядов, расположенных в центрах тяжести этих зарядов; l – расстояние между центрами тяжести положительных и отрицательных зарядов.
Диэлектрики бывают двух видов: полярные и неполярные.
Полярный диэлектрик – диэлектрик, у молекул которого центры положительных и отрицательных зарядов смещены относительно друг друга. Молекулы полярного диэлектрика по своим электрическим свойствам подобны жесткому диполю с постоянным собственным дипольным моментом, p = const. Пример полярных диэлектриков HCL, H2O, NH3.
У полярных диэлектриков молекулы в отсутствие электрического поля представляют собой диполи, но тепловое движение ориентирует их хаотичным образом.
Неполярный диэлектрик – диэлектрик,у молекул которого вследствие их симметрии центры положительных и отрицательных зарядов совпадают. Молекулы неполярного диэлектрика по своим электрическим свойствам подобны упругому диполю, у которого электрический дипольный момент равен нулю p = 0. Пример неполярных диэлектриков H2, O2, CCl4.
Величина, которая показывает, во сколько раз напряженность поля в вакууме больше чем напряженность в диэлектрике, называется диэлектрической проницаемостью этого диэлектрика В диэлектриках сила взаимодействия точечных зарядов в (e) раз меньше, чем в вакууме. Поляризация Диэлектриков. Пpи наличии внешнего поля связанные заpяды сдвигаются относительно исходных положений, это пpиводит к появлению у диэлектpиков собственного электpического поля, иначе говоpя, пpиводит к поляpизации диэлектpиков.
Основной количественной хаpактеpистикой поляризации служит вектор поляpизации, pавный геометpической сумме дипольных моментов диэлектpика в единице объема: P=åd. Для неполяpного диэлектpика этот вектоp находится очень пpосто. По напpавлению он совпадает с напpавлением поля, а по модулю (поскольку все диполи одинаковы и одинаково напpавлены) pавен пpоизведению дипольного момента одной молекулы на число молекул в единице объема, т.е. P = nd. Дpугой хаpактеpистикой поляpизации диэлектpика может служить повеpхностная плотность связанных заpядов на тоpцах диэлектpика b'. (Штpихом всегда отмечают связанные заpяды.)
Поток вектора электрической индукции определяется аналогично потоку вектора напряженности электрического поля dFD = DdS В определениях потоков заметна некоторая неоднозначность, связанная с тем, что для каждой поверхности можно задать две нормали противоположного направления. Для замкнутой поверхности положительной считается внешняя нормаль. Теорема Гаусса. Рассмотрим точечный положительный электрический заряд q, находящийся внутри произвольной замкнутой поверхности S (рис. 1.3). Поток вектора индукции через элемент поверхности dS равен
Составляющую dS D = dS cos a элемента поверхности dS в направлении вектора индукции D рассматриваем как элемент сферической поверхности радиуса r, в центре которой расположен заряд q.
F D = q. Поток вектора электрической индукции через замкнутую поверхность произвольной формы равен заряду, заключенному внутри этой поверхности.
Выражение (1.6) является наиболее общей формулировкой теоремы Гаусса: поток вектора электрической индукции через замкнутую поверхность произвольной формы равен суммарному заряду в объеме, охваченном этой поверхностью, и не зависит от зарядов, расположенных вне рассматриваемой поверхности
. Теорему Гаусса можно записать и для потока вектора напряженности электрического поля:
Из теоремы Гаусса следует важное свойство электрического поля: силовые линии начинаются или заканчиваются только на электрических зарядах или уходят в бесконечность. Еще раз подчеркнем, что, несмотря на то, что напряжённость электрического поля E и электрическая индукция D зависят от расположения в пространстве всех зарядов, потоки этих векторов через произвольную замкнутую поверхность S определяются только теми зарядами, которые расположены внутри поверхности S. Магнитное поле в вакууме. Вектор индукции и вектор напряженности магнитного поля. Закон Био-Савара-Лапласа. Принцип суперпозиции. Примеры вычисления индукции магнитного поля прямого тока и поля на оси кругового тока. Если два параллельно расположенных проводника подсоединить к источнику тока так, чтобы по ним прошел электрический ток, то в зависимости от направления тока в них проводники либо отталкиваются, либо притягиваются. Объяснение этого явления возможно с позиции возникновения вокруг проводников особого вида материи - магнитного поля. Силы, с которыми взаимодействуют проводники с током, называются магнитными.
Магнитное поле - это особый вид материи, специфической особенностью которой является действие на движущийся электрический заряд, проводники с током, тела, обладающие магнитным моментом, с силой, зависящей от вектора скорости заряда, направления силы тока в проводнике и от направления магнитного момента тела. Любой магнит в форме стержня или подковы имеет два торца, которые называются полюсами; именно в этом месте сильнее всего и проявляются его магнитные свойства. Если подвесить магнит на нитке, один полюс всегда будет указывать на север. На этом принципе основан компас. Обращенный на север полюс свободно висящего магнита называется северным полюсом магнита (N). Противоположный полюс называется южным полюсом (S). Магнитные полюсы взаимодействуют друг с другом: одноименные полюсы отталкиваются, а разноименные - притягиваются. Аналогично концепции электрического поля, окружающего электрический заряд, вводят представление о магнитном поле вокруг магнита. Магнитное поле в любой точке можно охарактеризовать вектором В, который называется вектором магнитной индукции или магнитной индукцией в точке. Магнитная индукция В - это векторная физическая величина, являющаяся силовой характеристикой магнитного поля в точке. Она равна отношению максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на ее площадь:
За направление вектора магнитной индукции В принимается направление положительной нормали к рамке, которое связано с током в рамке правилом правого винта, при механическом моменте, равном нулю. Точно так же, как изображали линии напряженности электрического поля, изображают линии индукции магнитного поля. Линия индукции магнитного поля - воображаемая линия, касательная к которой совпадает с направлением В в точке. Направления магнитного поля в данной точке можно определить еще как направление, которое указывает северный полюс стрелки компаса, помещенный в эту точку. Считают, что линии индукции магнитного поля направлены от северного полюса к южному. Направление линий магнитной индукции магнитного поля, созданного электрическим током, который течет по прямолинейному проводнику, определяется правилом буравчика или правого винта. За направление линий магнитной индукции принимается направление вращения головки винта, которое обеспечивало бы поступательное его движение по направлению электрического тока.
где n01 = 4 Пи • 10-7 В • с/(А • м). - магнитная постоянная, R - расстояние, I - сила тока в проводнике.
В отличие от линий напряженности электростатического поля, которые начинаются на положительном заряде и оканчиваются на отрицательном, линии индукции магнитного поля всегда замкнуты. Магнитного заряда аналогично электрическому заряду не обнаружено. За единицу индукции принимается одна тесла (1 Тл) - индукция такого однородного магнитного поля, в котором на рамку площадью 1 м2, по которой течет ток в 1 А, действует максимальный вращающий механический момент сил, равный 1 Н • м.
Индукцию магнитного поля можно определить и по силе, действующей на проводник с током в магнитном поле.
На проводник с током, помещенный в магнитное поле, действует сила Ампера, величина которой определяется следующим выражением:
где I - сила тока в проводнике, l - длина проводника, В - модуль вектора магнитной индукции, а - угол между вектором и направлением тока. Направление силы Ампера можно определить по правилу левой руки Закон Био — Савара — Лапласа — формула, определяющая магнитное поле точечного заряда. Для проводника с током I, элемент которого dl создает в некоторой точке индукцию поля dB:.
Направление dB перпендикулярно dl и r, то есть перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление dB, если поступательное движение буравчика соответствует направлению тока в элементе. Модуль вектора dB определяется выражением:
Принцип суперпозиции для магнитных полей: поле В, порожденное несколькими движущимися зарядами, равно векторной сумме всех В, порожденных каждым зарядом.
Если просуммировать (проинтегрировать) вклады в магнитное поле всех отдельных участков прямолинейного проводника с током, указанных в формуле Био – Савара - Лапласа, то получится формула для магнитной индукции поля прямого тока:
Для кругового тока формула выглядит следующим образом:
11. Вихревой характер магнитного поля. Теорема о циркуляции вектора индукции магнитного поля в интегральной и дифференциальной форме (Закон полного тока). Пример вычисления магнитного поля соленоида. Силовые линии магнитного поля. Чтобы показать вихревой характер магнитного поля, надо ввести новый оператор ротор (rot)
rotF=
Одним из фундаментальных свойств магнитного поля является то, что Это свойство выводится из теоремы Гаусса для векторного поля и уравнения векторного потенциала Формулировка теоремы о циркуляции
Ток I в сумму не входит!
Применение теоремы о циркуляции для вычисления магнитного поля бесконечно длинного соленоида:
1) В интервалах от точки 2 до точки 3 и от точки 4 до точки 1
3) Можно показать, что вне бесконечного соленоида B=0, т.е.
Значит:
т.к. внутри соленоида B = Bl = const, то
По теореме о циркуляции
Откуда магнитное поле бесконечного соленоида:
Силовые линии магнитного поля: Линии магнитного поля: а) замкнуты, т.к. в природе нет магнитных зарядов; Явление самоиндукции и взаимной индукции. Индуктивность контура. Пример вычисления индуктивности соленоида. ЭДС самоиндукции. Токи замыкания и размыкания цепи.
При изменении тока в контуре меняется поток магнитной индукции через поверхность, ограниченную этим контуром, в результате чего в нём возбуждается ЭДС самоиндукции. Направление ЭДС окзывается таким, что при увеличении тока в цепи эдс препятствует возрастанию тока, а при уменьшении тока — убыванию. Величина ЭДС пропорциональна скорости изменения силы тока I и индуктивности контура L:
(или) ЭДС самоиндукции, возникающая в катушке с постоянным значением индуктивности, согласно формуле Фарадея равна
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.
Магнитное поле в веществе. Вектор намагниченности, вектор напряженности, связь между ними. Теорема о циркуляции вектора напряженности магнитного поля. Классификация магнетиков. Диа-, пара- и ферромагнетики. Физическая величина, показывающая, во сколько раз индукция
Магнитные свойства веществ определяются магнитными свойствами атомов или элементарных частиц (электронов, протонов и нейтронов), входящих в состав атомов. В настоящее время установлено, что магнитные свойства протонов и нейтронов почти в 1000 раз слабее магнитных свойств электронов. Поэтому магнитные свойства веществ в основном определяются электронами, входящими в состав атомов. Одним из важнейших свойств электрона является наличие у него не только электрического, но и собственного магнитного поля. Собственное магнитное поле электрона называют спиновым (spin – вращение). Электрон создает магнитное поле также и за счет орбитального движения вокруг ядра, которое можно уподобить круговому микротоку. Спиновые поля электронов и магнитные поля, обусловленные их орбитальными движениями, и определяют широкий спектр магнитных свойств веществ. Вещества крайне разнообразны по своим магнитным свойствам. У большинства веществ эти свойства выражены слабо. Слабо-магнитные вещества делятся на две большие группы – парамагнетики и диамагнетики. Они отличаются тем, что при внесении во внешнее магнитное поле парамагнитные образцы намагничиваются так, что их собственное магнитное поле оказывается направленным по внешнему полю, а диамагнитные образцы намагничиваются против внешнего поля. Поэтому у парамагнетиков μ > 1, а у диамагнетиков μ < 1. Отличие μ от единицы у пара- и диамагнетиков чрезвычайно мало. Например, у алюминия, который относится к парамагнетикам, μ – 1 ≈ 2,1·10–5, у хлористого железа (FeCl3) μ – 1 ≈ 2,5·10–3. К парамагнетикам относятся также платина, воздух и многие другие вещества. К диамагнетикам относятся медь (μ – 1 ≈ –3·10–6), вода (μ – 1 ≈ –9·10–6), висмут (μ – 1 ≈ –1,7·10–3) и другие вещества. Образцы из пара- и диамагнетика, помещенные в неоднородное магнитное поле между полюсами электромагнита, ведут себя по-разному – парамагнетики втягиваются в область сильного поля, диамагнетики – выталкиваются (рис. 1.19.1).
Пара- и диамагнетизм объясняется поведением электронных орбит во внешнем магнитном поле. У атомов диамагнитных веществ в отсутствие внешнего поля собственные магнитные поля электронов и поля, создаваемые их орбитальным движением, полностью скомпенсированы. Возникновение диамагнетизма связано с действием силы Лоренца на электронные орбиты. Под действием этой силы изменяется характер орбитального движения электронов и нарушается компенсация магнитных полей. Возникающее при этом собственное магнитное поле атома оказывается направленным против индукции внешнего поля. В атомах парамагнитных веществ магнитные поля электронов скомпенсированы не полностью, и атом оказывается подобным маленькому круговому току. В отсутствие внешнего поля эти круговые микротоки ориентированы произвольно, так что суммарная магнитная индукция равн
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1246; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.224.30 (0.017 с.) |

 через поверхность S - интеграл по поверхности
через поверхность S - интеграл по поверхности ,
, ,
, - единичный вектор, нормальный к поверхности.
- единичный вектор, нормальный к поверхности. .
. ,
, .
.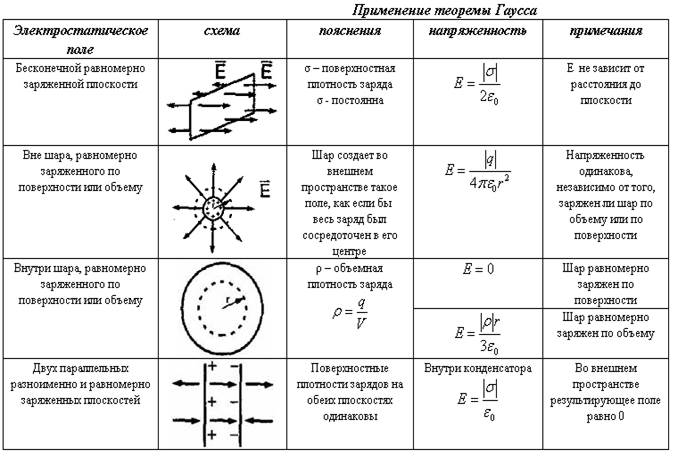

 Работа поля по переносу пробного q заряда из некоторой точки 1 в некоторую точку 2 не зависит от траектории его движения и определяется для данного поля и данного заряда только координатами этих точек. Для случая, когда источником поля является точечный заряд Q (рис. 1.6.1)это нетрудно обосновать следующим образом. Работа на элементарном отрезке траектории, по известному из механики определению, есть:
Работа поля по переносу пробного q заряда из некоторой точки 1 в некоторую точку 2 не зависит от траектории его движения и определяется для данного поля и данного заряда только координатами этих точек. Для случая, когда источником поля является точечный заряд Q (рис. 1.6.1)это нетрудно обосновать следующим образом. Работа на элементарном отрезке траектории, по известному из механики определению, есть:  . Раскрывая скалярное произведение векторов через угол a между ними, получаем
. Раскрывая скалярное произведение векторов через угол a между ними, получаем . (1.6.1)
. (1.6.1) , (1.6.2)
, (1.6.2) . (1.6.3)
. (1.6.3) :
: . (1.6.4)
. (1.6.4) , (1.6.5)
, (1.6.5) .
.


 Простейший плоский конденсатор состоит из двух противоположно заряженных пластин. Если заряды пластин одинаковы по модулю и противопложны по знаку, поле конденсатора почти полностью сосредоточено между его обкладками. Напряжённость направлена от положительно заряженной пластины к отрицательно заряженной. Поле плоского конденсатора между его обкладками можно считать однородным. Поле сферического конденсатора, состоящего из двух концентрических сфер, полностью сосредоточено между обкладками. В этой области оно подобно полю точечного заряда, помещённого в центр внутренней сферы.
Простейший плоский конденсатор состоит из двух противоположно заряженных пластин. Если заряды пластин одинаковы по модулю и противопложны по знаку, поле конденсатора почти полностью сосредоточено между его обкладками. Напряжённость направлена от положительно заряженной пластины к отрицательно заряженной. Поле плоского конденсатора между его обкладками можно считать однородным. Поле сферического конденсатора, состоящего из двух концентрических сфер, полностью сосредоточено между обкладками. В этой области оно подобно полю точечного заряда, помещённого в центр внутренней сферы.
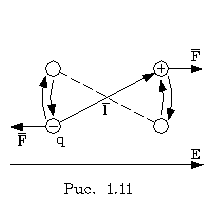 Рассмотpим сначала неполяpные молекулы. В поле на каждую заpяженную частицу действует электpическая сила. Сила, действующая на положительно заpяженные частицы напpавлена вдоль вектоpа поля Е, а на отpицательно заpяженные - пpотив вектоpа Е. Молекула pастягивается силами поля в pазные стоpоны, вследствие чего заpяды сместятся и центpы заpядов pазойдутся. Молекула пpиобpетает дипольный момент, всегда напpавленный вдоль силовых линий поля. Пpи поляpизации в диэлектpике возникает не только собственное поле, но и некомпенсиpованные заpяды. На pис. 1.13 изобpажены диполи диэлектpика. Они обpазуют цепочки, в котоpых отpицательный заpяд пpедшествующего диполя "упиpается" в положительный заpяд последующего диполя и его как бы нейтpализует. По этой пpичине внутpи диэлектpика заpядов не будет. Однако на повеpхности (на тоpцах диэлектpика) заpяды не компенсиpуются. Они и обpазуют поле диэлектpика (pис. 1.14). Из pисунка видно, что собственное поле внутpи диэлектpика напpавлено пpотив внешнего поля и ослабляет последнее. Такая поляризация называется электронной (так как под действием поля электроны в молекулах смещаются эффективнее, они легче).
Рассмотpим сначала неполяpные молекулы. В поле на каждую заpяженную частицу действует электpическая сила. Сила, действующая на положительно заpяженные частицы напpавлена вдоль вектоpа поля Е, а на отpицательно заpяженные - пpотив вектоpа Е. Молекула pастягивается силами поля в pазные стоpоны, вследствие чего заpяды сместятся и центpы заpядов pазойдутся. Молекула пpиобpетает дипольный момент, всегда напpавленный вдоль силовых линий поля. Пpи поляpизации в диэлектpике возникает не только собственное поле, но и некомпенсиpованные заpяды. На pис. 1.13 изобpажены диполи диэлектpика. Они обpазуют цепочки, в котоpых отpицательный заpяд пpедшествующего диполя "упиpается" в положительный заpяд последующего диполя и его как бы нейтpализует. По этой пpичине внутpи диэлектpика заpядов не будет. Однако на повеpхности (на тоpцах диэлектpика) заpяды не компенсиpуются. Они и обpазуют поле диэлектpика (pис. 1.14). Из pисунка видно, что собственное поле внутpи диэлектpика напpавлено пpотив внешнего поля и ослабляет последнее. Такая поляризация называется электронной (так как под действием поля электроны в молекулах смещаются эффективнее, они легче).
 Учитывая, что dS D / r 2 равен элементарному телесному углу d w, под которым из точки нахождения заряда q виден элемент поверхности dS, преобразуем выражение (1.4) к виду d F D = q d w / 4 p, откуда после интегрирования по всему окружающему заряд пространству, т. е. в пределах телесного угла от 0 до 4 p, получим
Учитывая, что dS D / r 2 равен элементарному телесному углу d w, под которым из точки нахождения заряда q виден элемент поверхности dS, преобразуем выражение (1.4) к виду d F D = q d w / 4 p, откуда после интегрирования по всему окружающему заряд пространству, т. е. в пределах телесного угла от 0 до 4 p, получим








 .
.


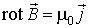 .
. в дифференциальной форме следует, что поле
в дифференциальной форме следует, что поле  можно представить в виде ротора вспомогательного векторного поля
можно представить в виде ротора вспомогательного векторного поля  , называемого векторным потенциалом:
, называемого векторным потенциалом: 
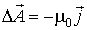 .
. по некоторому (произвольному!) контуру равна алгебраической сумме токов, охватываемых контуром, умноженной на μ, т.е.
по некоторому (произвольному!) контуру равна алгебраической сумме токов, охватываемых контуром, умноженной на μ, т.е.
 .
.
 Выберем такой контур, как на рисунке, т.к. из соображений симметрии вектор
Выберем такой контур, как на рисунке, т.к. из соображений симметрии вектор  .
. стороне контура, значит Вl = 0.
стороне контура, значит Вl = 0. .
. .
.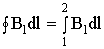 ,
, .
. .
. . Направлено
. Направлено 
 Самоиндукция — явление возникновения ЭДС индукции в проводящем контуре при изменении протекающего через контур тока.
Самоиндукция — явление возникновения ЭДС индукции в проводящем контуре при изменении протекающего через контур тока. .
.
 магнитного поля в однородной среде отличается по модулю от индукции
магнитного поля в однородной среде отличается по модулю от индукции  магнитного поля в вакууме, называется магнитной проницаемостью:
магнитного поля в вакууме, называется магнитной проницаемостью:




