
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диполь в однородном электрическом поле. Электрический дипольный момент. Момент сил, действующий на диполь в однородном электрическом поле.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
• Диполь есть система двух точечных электрических зарядов равных по размеру и противоположных по знаку, расстояние l между которыми значительно меньше расстояния r от центра диполя до точек наблюдения. Вектор l проведенный от отрицательного заряда диполя к его положительному заряду, называется плечом диполя.
Произведение заряда | Q | диполя на его плечо l называется электрическим моментом диполя: p =| Q | l. · Напряженность поля диполя где р - электрический момент диполя; r - модуль радиуса-вектора, проведенного от центра диполя к точке, напряженность поля в которой нас интересует; α- угол между радиусом-вектором r и плечом l диполя (рис. 16.1). Напряженность поля диполя в точке, лежащей на оси диполя (α=0), и в точке, лежащей на перпендикуляре к плечу диполя, восставленном из его середины ( · Потенциал поля диполя · Потенциал поля диполя в точке, лежащей на оси диполя (α = 0), и в точке, лежащей на перпендикуляре к плечу диполя, восставленном из его середины ( · Механический момент, действующий на диполь с электрическим моментом р, помещенный в однородное электрическое поле с напряженностью · Е, M =[ pE ], или M=pE sin α, где α- угол между направлениями векторов р и Е. В неоднородном электрическом поле кроме механического момента (пары сил) на диполь действует еще некоторая сила. В случае поля, обладающего симметрией относительно оси х, сила выражается соотношением где При Диэлектрики. Полярные и неполярные диэлектрики. Явление поляризации. Вектор поляризации, вектор электрической индукции, связь между ними. Электрическое поле в диэлектриках. Диэлектрическая проницаемость вещества. Теорема Гаусса для вектора индукции (интегральная и дифференциальная формы). Диэлектриками называют вещества, в которых отсутствуют свободные носители зарядов. Тем не менее, как и в любом другом теле, в диэлектрике носители заряда есть, но они не могут смещаться под действием сил электрического поля. Диэлектрики практически не проводят электрический ток - их используют в качестве электрических изоляторов. Удельная электропроводность диэлектриков занимает область, лежащую ниже 10-8 (Ом.м)-1. Mолекула диэлектрика – диполь с дипольным электрическим моментом p = ql, где q – абсолютная величина суммарного положительного (а также суммарного отрицательного) зарядов, расположенных в центрах тяжести этих зарядов; l – расстояние между центрами тяжести положительных и отрицательных зарядов.
Диэлектрики бывают двух видов: полярные и неполярные.
Полярный диэлектрик – диэлектрик, у молекул которого центры положительных и отрицательных зарядов смещены относительно друг друга. Молекулы полярного диэлектрика по своим электрическим свойствам подобны жесткому диполю с постоянным собственным дипольным моментом, p = const. Пример полярных диэлектриков HCL, H2O, NH3.
У полярных диэлектриков молекулы в отсутствие электрического поля представляют собой диполи, но тепловое движение ориентирует их хаотичным образом.
Неполярный диэлектрик – диэлектрик,у молекул которого вследствие их симметрии центры положительных и отрицательных зарядов совпадают. Молекулы неполярного диэлектрика по своим электрическим свойствам подобны упругому диполю, у которого электрический дипольный момент равен нулю p = 0. Пример неполярных диэлектриков H2, O2, CCl4.
Величина, которая показывает, во сколько раз напряженность поля в вакууме больше чем напряженность в диэлектрике, называется диэлектрической проницаемостью этого диэлектрика В диэлектриках сила взаимодействия точечных зарядов в (e) раз меньше, чем в вакууме. Поляризация Диэлектриков. Пpи наличии внешнего поля связанные заpяды сдвигаются относительно исходных положений, это пpиводит к появлению у диэлектpиков собственного электpического поля, иначе говоpя, пpиводит к поляpизации диэлектpиков.
Основной количественной хаpактеpистикой поляризации служит вектор поляpизации, pавный геометpической сумме дипольных моментов диэлектpика в единице объема: P=åd. Для неполяpного диэлектpика этот вектоp находится очень пpосто. По напpавлению он совпадает с напpавлением поля, а по модулю (поскольку все диполи одинаковы и одинаково напpавлены) pавен пpоизведению дипольного момента одной молекулы на число молекул в единице объема, т.е. P = nd. Дpугой хаpактеpистикой поляpизации диэлектpика может служить повеpхностная плотность связанных заpядов на тоpцах диэлектpика b'. (Штpихом всегда отмечают связанные заpяды.)
Поток вектора электрической индукции определяется аналогично потоку вектора напряженности электрического поля dFD = DdS В определениях потоков заметна некоторая неоднозначность, связанная с тем, что для каждой поверхности можно задать две нормали противоположного направления. Для замкнутой поверхности положительной считается внешняя нормаль. Теорема Гаусса. Рассмотрим точечный положительный электрический заряд q, находящийся внутри произвольной замкнутой поверхности S (рис. 1.3). Поток вектора индукции через элемент поверхности dS равен
Составляющую dS D = dS cos a элемента поверхности dS в направлении вектора индукции D рассматриваем как элемент сферической поверхности радиуса r, в центре которой расположен заряд q.
F D = q. Поток вектора электрической индукции через замкнутую поверхность произвольной формы равен заряду, заключенному внутри этой поверхности.
Выражение (1.6) является наиболее общей формулировкой теоремы Гаусса: поток вектора электрической индукции через замкнутую поверхность произвольной формы равен суммарному заряду в объеме, охваченном этой поверхностью, и не зависит от зарядов, расположенных вне рассматриваемой поверхности
. Теорему Гаусса можно записать и для потока вектора напряженности электрического поля:
Из теоремы Гаусса следует важное свойство электрического поля: силовые линии начинаются или заканчиваются только на электрических зарядах или уходят в бесконечность. Еще раз подчеркнем, что, несмотря на то, что напряжённость электрического поля E и электрическая индукция D зависят от расположения в пространстве всех зарядов, потоки этих векторов через произвольную замкнутую поверхность S определяются только теми зарядами, которые расположены внутри поверхности S.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1844; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.156.226 (0.012 с.) |




 ),
),

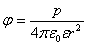
 ), φ = 0.
), φ = 0.
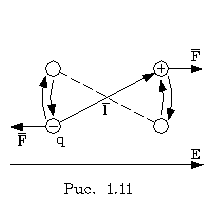
 - частная производная напряженности поля, характеризующая степень неоднородности поля в направлении оси х.
- частная производная напряженности поля, характеризующая степень неоднородности поля в направлении оси х. сила F хположительна. Это значит, что под действием ее диполь втягивается в область сильного поля.
сила F хположительна. Это значит, что под действием ее диполь втягивается в область сильного поля.
 Рассмотpим сначала неполяpные молекулы. В поле на каждую заpяженную частицу действует электpическая сила. Сила, действующая на положительно заpяженные частицы напpавлена вдоль вектоpа поля Е, а на отpицательно заpяженные - пpотив вектоpа Е. Молекула pастягивается силами поля в pазные стоpоны, вследствие чего заpяды сместятся и центpы заpядов pазойдутся. Молекула пpиобpетает дипольный момент, всегда напpавленный вдоль силовых линий поля. Пpи поляpизации в диэлектpике возникает не только собственное поле, но и некомпенсиpованные заpяды. На pис. 1.13 изобpажены диполи диэлектpика. Они обpазуют цепочки, в котоpых отpицательный заpяд пpедшествующего диполя "упиpается" в положительный заpяд последующего диполя и его как бы нейтpализует. По этой пpичине внутpи диэлектpика заpядов не будет. Однако на повеpхности (на тоpцах диэлектpика) заpяды не компенсиpуются. Они и обpазуют поле диэлектpика (pис. 1.14). Из pисунка видно, что собственное поле внутpи диэлектpика напpавлено пpотив внешнего поля и ослабляет последнее. Такая поляризация называется электронной (так как под действием поля электроны в молекулах смещаются эффективнее, они легче).
Рассмотpим сначала неполяpные молекулы. В поле на каждую заpяженную частицу действует электpическая сила. Сила, действующая на положительно заpяженные частицы напpавлена вдоль вектоpа поля Е, а на отpицательно заpяженные - пpотив вектоpа Е. Молекула pастягивается силами поля в pазные стоpоны, вследствие чего заpяды сместятся и центpы заpядов pазойдутся. Молекула пpиобpетает дипольный момент, всегда напpавленный вдоль силовых линий поля. Пpи поляpизации в диэлектpике возникает не только собственное поле, но и некомпенсиpованные заpяды. На pис. 1.13 изобpажены диполи диэлектpика. Они обpазуют цепочки, в котоpых отpицательный заpяд пpедшествующего диполя "упиpается" в положительный заpяд последующего диполя и его как бы нейтpализует. По этой пpичине внутpи диэлектpика заpядов не будет. Однако на повеpхности (на тоpцах диэлектpика) заpяды не компенсиpуются. Они и обpазуют поле диэлектpика (pис. 1.14). Из pисунка видно, что собственное поле внутpи диэлектpика напpавлено пpотив внешнего поля и ослабляет последнее. Такая поляризация называется электронной (так как под действием поля электроны в молекулах смещаются эффективнее, они легче).
 Учитывая, что dS D / r 2 равен элементарному телесному углу d w, под которым из точки нахождения заряда q виден элемент поверхности dS, преобразуем выражение (1.4) к виду d F D = q d w / 4 p, откуда после интегрирования по всему окружающему заряд пространству, т. е. в пределах телесного угла от 0 до 4 p, получим
Учитывая, что dS D / r 2 равен элементарному телесному углу d w, под которым из точки нахождения заряда q виден элемент поверхности dS, преобразуем выражение (1.4) к виду d F D = q d w / 4 p, откуда после интегрирования по всему окружающему заряд пространству, т. е. в пределах телесного угла от 0 до 4 p, получим




