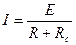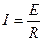Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дипольный эквивалентный генераторСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Потенциал точки поля диполя. Согласно уравнения (1) потенциал поля, создаваемого диполем, определяется выражением Найдем более подробный вид этого выражения, исходя из того, что диполь состоит из двух точечных зарядов. В среде с диэлектрической проницаемостью Е потенциал электрического поля, создаваемого точечным зарядом q на расстоянии r определяется по формуле:
В некоторой точке А, удаленной от зарядов соответственно на расстоянии r и r1 (рис.3) потенциалы зарядов будут складываться. Применяя к каждому заряду формулу (3) с учетом знаков зарядов и приводя слагаемые к общему знаменателю, получим потенциал диполя в целом.
Учитывая, что L<<r и L<<r1 можем приближенно считать, что r=r1, r*r1=r2 и r-r1=L*Cos α. Подставим эти результаты в формулу (4) и с учетом формулы (2) получим:
Таким образом, потенциал поля диполя в некоторой точке А прямо пропорционален моменту диполя Р и зависит от угла α между вектором Р и направлением от диполя на точку А. Кроме того потенциал зависит от расстояния (
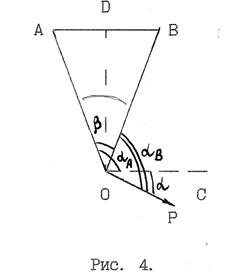
Разность потенциалов двух точек поля диполя. Пусть диполь, плечо которого мало (L→0) находится в точке 0 (рис.4). Вектор Р – электрический момент диполя.
Обозначим угол между вектором Р и направлением АВ
Учитывая эти равенства, выразим αв=α+
Тогда Cos (αв) – Соs(αA) =-2Sin((αB+αA)/2)*Sin((αB-αA)/2)= -2Sin(α+π/2)*Sin(-ß/2)=2Sin(ß/2)*Cos(α). Подставляя эту формулу в выражение (6), получим: UAB= φB-φA=
Таким образом, создаваемая диполем разность потенциалов двух точек прямо пропорциональна проекции электрического момента диполя, РСоsα на прямую, проходящую через точки А и В. Кроме того она зависит от свойств среды (ε), расстояния этих точек от диполя (~ Все эти зависимости будут использованы при введении понятия треугольника Эйнтховена(раздел 6.3) З. Токовый диполь
В организме сердце окружено другими органами и тканями, которые обладают некоторой электропроводностью. Поэтому, согласно принципу анатомо-физиологического соответствия, эквивалентный элект р ический генератор сердца следует считать расположенным в токопроводящей среде. Будучи помещенным в токопроводящую среду, заряд становится источником тока (рис 5) и через окружающую унидиполь сферу произвольного радиуса r будет протекать выходящий из него ток I. Потенциал, создаваемый униполем как генератором тока, определяется по формуле
где ρ – удельное сопротивление среды. Из сравнения формул (8) и (3) видно, что для токового униполя существует такой же характер зависимости потенциала от расстояния, как и для токового заряда в диэлектрической среде
Это значит, что повторив рассуждения, проделанные нами при выводе формул (5)-(7), мы и для токового диполя получим формулы с аналогичными зависимостями от углов и расстояний. Однако, влияние сопротивления проводящей среды надо рассматривать отдельно. Эквивалентная схема токового генератора во внешней проводящей среде представлена на рис.6. Здесь Rc - cопротивление внешней среды, R – внутреннее сопротивление токового генератора, Е – э.д.с. генератора, I – сила тока в цепи. По закону Ома для полной цепи сила суммарного тока в среде равна силе тока в генераторе и вычисляется по формуле:
Так как сопротивление мембран, на которых фактически генерируется разность потенциалов, во много раз больше сопротивления межклеточной жидкости(R>>Rc), то сопротивлением Rc можно пренебречь
Это значит, что сила тока в данной среде не зависит от сопротивления внешней среды, поэтому неоднородностями сопротивления окружающей среды можно пренебречь и считать, что оно расположено в однородной токопроводящей среде.
Основные положения теории Эйнтховена.
|
|||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 890; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.241.170 (0.011 с.) |

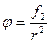
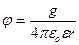 (3)
(3)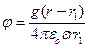 (4)
(4)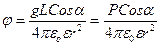 (5)
(5)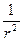 ) и свойств среды ε.
) и свойств среды ε.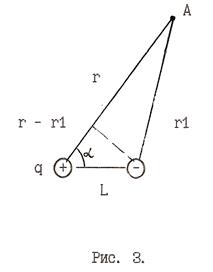



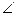 αА -
αА - 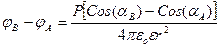 (6)
(6)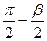
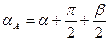
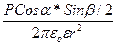 (7)
(7)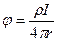 (8)
(8)