
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энергия системы зарядов. Энергия плоского конденсатора. Энергия электростатического поля. Объемная плотность энергии.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Потенциальную энергию взаимодействия двух точечных зарядов q1 и q2, находящихся в вакууме на расстоянии r12 друг от друга можно вычислить по:
Рассмотрим систему, состоящую из N точечных зарядов: q1, q2,..., qn.
Энергия взаимодействия такой системы равна сумме энергий взаимодействия зарядов взятых попарно:
В формуле 2 суммирование производится по индексам i и k (i№k). Оба индекса пробегают, независимо друг от друга, значения от 0 до N. Слагаемые, для которых значение индекса i совпадает со значением индекса k не учитываются. Коэффициент 1/2 поставлен потому, что при суммировании потенциальная энергия каждой пары зарядов учитывается дважды. Формулу (2) можно представить в виде:
где ji - потенциал в точке нахождения i-го заряда, создаваемый всеми остальными зарядами:
Энергия взаимодействия системы точечных зарядов, вычисляемая по формуле (3), может быть как положительной, так и отрицательной. Например она отрицательная для двух точечных зарядов противоположного знака.
Формула (3) определяет не полную электростатическую энергию системы точечных зарядов, а только их взаимную потенциальную энергию. Каждый заряд qi, взятый в отдельности обладает электрической энергией. Она называется собственной энергией заряда и представляет собой энергию взаимного отталкивания бесконечно малых частей, на которые его можно мысленно разбить. Эта энергия не учитывается в формуле (3). Учитывается только работа затрачиваемая на сближение зарядов qi, но не на их образование.
Полная электростатическая энергия системы точечных зарядов учитывает также работу, на образование зарядов qiиз бесконечно малых порций электричества, переносимых из бесконечности. Полная электростатическая энергия системы зарядов всегда положительная. Это легко показать на примере заряженного проводника. Рассматривая заряженный проводник как систему точечных зарядов и учитывая одинаковое значение потенциала в любой точке проводника, из формулы (3) получим: Эта формула дает полную энергию заряженного проводника, которая всегда положительна (при q>0, j>0, следовательно W>0, если q<0, то j<0, но W>0). Энергия заряженного плоского конденсатора Eк равна работе A, которая была затрачена при его зарядке, или совершается при его разрядке.
A = CU2/2 = Q2/2С = QU/2 = Eк.
Поскольку напряжение на конденсаторе может быть рассчитано из соотношения:
U = E*d, где E - напряженность поля между обкладками конденсатора, d - расстояние между пластинами конденсатора,
то энергия заряженного конденсатора равна:
Eк = CU2/2 = ee0S/2d*E2*d2 = ee0S*d*E2/2 = ee0V*E2/2, где V - объем пространства между обкладками конденсатора.
Энергия заряженного конденсатора сосредоточена в его электрическом поле. энергия конденсатора – это, на самом деле, энергия электростатического поля, энергия принадлежит полю, ни обкладкам конденсатора, ни заряду.
объёмная плотность энергии w представляет собой сумму плотностей собственно электромагнитной энергии и энергии материальной среды, обусловленной электромагнитным полем.
При линейной зависимости между W= Где
Магнитное поле в вакууме. Вектор индукции и вектор напряженности магнитного поля. Закон Био-Савара-Лапласа. Принцип суперпозиции. Примеры вычисления индукции магнитного поля прямого тока и поля на оси кругового тока. Если два параллельно расположенных проводника подсоединить к источнику тока так, чтобы по ним прошел электрический ток, то в зависимости от направления тока в них проводники либо отталкиваются, либо притягиваются. Объяснение этого явления возможно с позиции возникновения вокруг проводников особого вида материи - магнитного поля. Силы, с которыми взаимодействуют проводники с током, называются магнитными.
Магнитное поле - это особый вид материи, специфической особенностью которой является действие на движущийся электрический заряд, проводники с током, тела, обладающие магнитным моментом, с силой, зависящей от вектора скорости заряда, направления силы тока в проводнике и от направления магнитного момента тела. Любой магнит в форме стержня или подковы имеет два торца, которые называются полюсами; именно в этом месте сильнее всего и проявляются его магнитные свойства. Если подвесить магнит на нитке, один полюс всегда будет указывать на север. На этом принципе основан компас. Обращенный на север полюс свободно висящего магнита называется северным полюсом магнита (N). Противоположный полюс называется южным полюсом (S).
Магнитные полюсы взаимодействуют друг с другом: одноименные полюсы отталкиваются, а разноименные - притягиваются. Аналогично концепции электрического поля, окружающего электрический заряд, вводят представление о магнитном поле вокруг магнита. Магнитное поле в любой точке можно охарактеризовать вектором В, который называется вектором магнитной индукции или магнитной индукцией в точке. Магнитная индукция В - это векторная физическая величина, являющаяся силовой характеристикой магнитного поля в точке. Она равна отношению максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на ее площадь:
За направление вектора магнитной индукции В принимается направление положительной нормали к рамке, которое связано с током в рамке правилом правого винта, при механическом моменте, равном нулю. Точно так же, как изображали линии напряженности электрического поля, изображают линии индукции магнитного поля. Линия индукции магнитного поля - воображаемая линия, касательная к которой совпадает с направлением В в точке. Направления магнитного поля в данной точке можно определить еще как направление, которое указывает северный полюс стрелки компаса, помещенный в эту точку. Считают, что линии индукции магнитного поля направлены от северного полюса к южному. Направление линий магнитной индукции магнитного поля, созданного электрическим током, который течет по прямолинейному проводнику, определяется правилом буравчика или правого винта. За направление линий магнитной индукции принимается направление вращения головки винта, которое обеспечивало бы поступательное его движение по направлению электрического тока.
где n01 = 4 Пи • 10-7 В • с/(А • м). - магнитная постоянная, R - расстояние, I - сила тока в проводнике.
В отличие от линий напряженности электростатического поля, которые начинаются на положительном заряде и оканчиваются на отрицательном, линии индукции магнитного поля всегда замкнуты. Магнитного заряда аналогично электрическому заряду не обнаружено. За единицу индукции принимается одна тесла (1 Тл) - индукция такого однородного магнитного поля, в котором на рамку площадью 1 м2, по которой течет ток в 1 А, действует максимальный вращающий механический момент сил, равный 1 Н • м.
Индукцию магнитного поля можно определить и по силе, действующей на проводник с током в магнитном поле.
На проводник с током, помещенный в магнитное поле, действует сила Ампера, величина которой определяется следующим выражением:
где I - сила тока в проводнике, l - длина проводника, В - модуль вектора магнитной индукции, а - угол между вектором и направлением тока. Направление силы Ампера можно определить по правилу левой руки Закон Био — Савара — Лапласа — формула, определяющая магнитное поле точечного заряда. Для проводника с током I, элемент которого dl создает в некоторой точке индукцию поля dB:.
Направление dB перпендикулярно dl и r, то есть перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление dB, если поступательное движение буравчика соответствует направлению тока в элементе. Модуль вектора dB определяется выражением:
Принцип суперпозиции для магнитных полей: поле В, порожденное несколькими движущимися зарядами, равно векторной сумме всех В, порожденных каждым зарядом.
Если просуммировать (проинтегрировать) вклады в магнитное поле всех отдельных участков прямолинейного проводника с током, указанных в формуле Био – Савара - Лапласа, то получится формула для магнитной индукции поля прямого тока:
Для кругового тока формула выглядит следующим образом:
11. Вихревой характер магнитного поля. Теорема о циркуляции вектора индукции магнитного поля в интегральной и дифференциальной форме (Закон полного тока). Пример вычисления магнитного поля соленоида. Силовые линии магнитного поля. Чтобы показать вихревой характер магнитного поля, надо ввести новый оператор ротор (rot)
rotF=
Одним из фундаментальных свойств магнитного поля является то, что Это свойство выводится из теоремы Гаусса для векторного поля и уравнения векторного потенциала Формулировка теоремы о циркуляции
Ток I в сумму не входит!
Применение теоремы о циркуляции для вычисления магнитного поля бесконечно длинного соленоида:
1) В интервалах от точки 2 до точки 3 и от точки 4 до точки 1
3) Можно показать, что вне бесконечного соленоида B=0, т.е.
Значит:
т.к. внутри соленоида B = Bl = const, то
По теореме о циркуляции
Откуда магнитное поле бесконечного соленоида:
Силовые линии магнитного поля:
Линии магнитного поля: а) замкнуты, т.к. в природе нет магнитных зарядов;
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1004; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.10.207 (0.012 с.) |

 (1)
(1) (2)
(2) (3)
(3)



 и
и  , а также
, а также  и
и  (это имеет место в вакууме и линейных средах) имеем
(это имеет место в вакууме и линейных средах) имеем
 и
и  — вектор электрического смещения (индукции),
— вектор электрического смещения (индукции),  — вектор индукции магнитного поля.
— вектор индукции магнитного поля.






 .
.


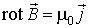 .
. в дифференциальной форме следует, что поле
в дифференциальной форме следует, что поле  можно представить в виде ротора вспомогательного векторного поля
можно представить в виде ротора вспомогательного векторного поля  , называемого векторным потенциалом:
, называемого векторным потенциалом: 
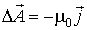 .
. по некоторому (произвольному!) контуру равна алгебраической сумме токов, охватываемых контуром, умноженной на μ, т.е.
по некоторому (произвольному!) контуру равна алгебраической сумме токов, охватываемых контуром, умноженной на μ, т.е.
 .
.
 Выберем такой контур, как на рисунке, т.к. из соображений симметрии вектор
Выберем такой контур, как на рисунке, т.к. из соображений симметрии вектор  .
. стороне контура, значит Вl = 0.
стороне контура, значит Вl = 0. .
. .
.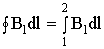 ,
, .
. .
. . Направлено
. Направлено 



