
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос №6 Электрическое полеСодержание книги
Поиск на нашем сайте ЭЛЕКТРИЧЕСКИМ ПОЛЕМ (ЭП) называется то, что существует в области пространства, в которой на электрически заряженную частицу действует сила, называемая электрической (кулоновской). ИСТОЧНИКОМ ЭП являются электрически заряженные частицы. ЗАРЯДОМ (электрическим) называется особая характеристика объекта, определяющая его способность создавать ЭП и взаимодействовать с ЭП. Часто «зарядом» называют заряженную частицу, а «точечным зарядом» - материальную точку, имеющую электрический заряд. Основные СВОЙСТВА электрического заряда: 1. Заряд ИНВАРИАНТЕН – его величина одинакова при измерении в любой инерциальной системе отсчета. 2. Заряд СОХРАНЯЕТСЯ – суммарный заряд изолированной системы тел не изменяется. 3. Заряд АДДИТИВЕН – заряд системы тел равен сумме зарядов отдельных тел. 4. Заряд ДИСКРЕТЕН – заряд любого тела по величине кратен минимальному заряду, который обозначается символом е и равен 1.6 10-19 Кл. 5. Существуют заряды ДВУХ разных «сортов». Заряды одного «сорта» названы положительными, а другого «сорта» -отрицательными. Одноименные заряды отталкиваются, а разноименные – притягиваются. Если вблизи одной заряженной частицы (заряда Q1), расположенной в начале координат, будет находиться вторая заряженная частица (заряд Q2), то на второй заряд будет действовать электрическая (кулоновская) НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ – характеристика силового действия ЭП на заряд. Напряженность ЭП,создаваемого зарядом Q1 , есть векторная величина, обозначаемая символом ЛИНИЯ ЭП – линия, в любой точке которой вектор напряженности ЭП направлен по касательной к ней. ЭП подчиняется ПРИНЦИПУ СУПЕРПОЗИЦИИ: напряженность ЭП нескольких источников является суммой векторов напряженности поля, создаваемого независимо каждым источником ПОТОКОМ ЭП называется интеграл по некоторой поверхности S от скалярного произведения напряженности ЭП на элемент поверхности: ЗАКОН ГАУССА ДЛЯ ЭП: ПОТОК ЭП через замкнутую поверхность S0 пропорционален суммарному ЗАРЯДУ, расположенному внутри объема, ограниченного поверхностью интегрирования потока V(S0): Линии напряженности электрического поля точечного заряда представляют собой прямые линии, идущие от заряда (положительного) или к заряду. ПОТЕНЦИАЛОМ данной точки
ДИПОЛЬ есть два одинаковых по величине, но противоположных по знаку точечных зарядов Q, расположенных на расстоянии L (L — плечо диполя). ДИПОЛЬНЫЙ (ЭЛЕКТРИЧЕСКИЙ) МОМЕНТ есть произведение Напряженность ЭП диполя вычисляется с использованием принципа суперпозиции для ЭП. Как видно из рисунка, а для суммарной силы получим На линии, проходящей через центр диполя, перпендикулярно электрическому моменту, и на большом расстоянии r от его центра:
Вопрос №9 Напряженность и потенциал однородно заряженной плоскости, бесконечного проводника и бесконечных разноименно заряженных плоскостей. Бесконечная плоскость заряжена с поверхностной плотностью зарядов s=dq/dS. Линии напряженности перпендикулярны плоскости и направлены в обе стороны от плоскости. В качестве замкнутой поверхности выберем поверхность цилиндра, основания которого параллельны бесконечной плоскости, а ось цилиндра ^ плоскости. Т.к. образующие цилиндра параллельны линиям напряженности(a=0,cosa=1), то поток вектора напряженности сквозь боковую поверхность равен 0, а полный поток сквозь цилиндрическую поверхность равен сумме потоков сквозь его основания. Для основания: Еn = E. Заряд, заключенный внутри построенной замкнутой поверхности, равен: s Sосн. Отсюда численная величина потока равна: Ф Е = Е 2 Sосн.. По теореме Гаусса: Ф Е = q/ε0 = σ*Sосн / ε0, тогда: E=S/2 ε0, не зависит от длины цилиндра и на любых расстояниях от плоскости одинакова по модулю. Поле равномерно заряженной плоскости однородно.
Где, σ = q / S – поверхностная плотность заряда. Чтобы получить выражение для потенциала между плоскостями, проинтегрируем выражение
При x 1 = 0 и x 2 = d На рисунке изображена зависимость напряженности E и потенциала φ от расстояния между плоскостями.
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 257; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

 , определяемая законом Кулона:
, определяемая законом Кулона: 
 тогда
тогда 
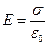 – напряженность электростатического поля между заряженными плоскостями
– напряженность электростатического поля между заряженными плоскостями







