
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос№14 Безвихревой характер электростатического поля
Работа, совершенная силами поля при перемещении заряда q из точки 1 в точку 2 определяется как Работа сил поля вдоль замкнутой кривой равна нулю. Для этого необходимо доказать, что циркуляция вектора Е равна нулю
В случае точечного заряда Так как Пользуясь теоремой Стокса Получаем
Это соотношение выражает основное свойство электростатического поля - оно безвихревое. Вопрос №15 Проводники в электростатическом поле При внесении незаряженного проводника в электрическое поле носители заряда приходят в движение: положительные в направление вектора
В металлических проводниках подвижными носителями заряда являются электроны, заряд которых является отрицательным. Поэтому электроны устремляются в направлении, противоположном направлению вектора Индуцированные заряды распределяются по внешней поверхности проводника. Если внутри проводника имеется полость, то при равновесном распределении индуцированных зарядов поле внутри нее также обращается в нуль. На этом основывается электростатическая защита. Когда какой – то прибор необходимо защитить от воздействия внешних полей, его окружают проводящим футляром (экраном). Внешнее поле компенсируется индуцированными зарядами. Подобный экран действует хорошо и в том случае, если его сделать не сплошным, а в виде густой сетки.
Таким образом, при внесении незаряженного проводника во внешнее электростатическое поле на поверхности проводника индуцируются заряды. Суммарный заряд проводника равен нулю. Равновесие зарядов на проводнике может наблюдаться лишь при выполнении следующих условий: 1. Напряженность электрического поля внутри проводника должна быть равна нулю.
В соответствии с формулой (33) 2. Напряженность поля на поверхности проводника должна быть направлена по нормали к поверхности, т.е.
Следовательно, в случае равновесия зарядов поверхность проводника будет эквипотенциальной. Можно доказать это последнее утверждение формально: проведем внутри проводника произвольную замкнутую поверхность S, ограничив некоторый объем внутри проводника. Тогда, согласно теореме Остроградского-Гаусса, суммарный заряд q этого объема равен нулю
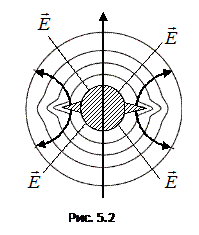
3. Если проводнику сообщить некоторый заряд q, то он распределится так, чтобы соблюдались условия равновесия заряда. Это означает, что ни в каком месте внутри проводника и на его поверхности избыточные заряды располагаться не могут, так как одноименные заряды, образующие данный заряд q, взаимно отталкиваются и стремятся расположиться на наибольшем расстоянии друг от друга. В заряженном проводнике некомпенсированные заряды располагаются только на поверхности (их расталкивают кулоновские силы). Рассмотрим поле, создаваемое изображенным на рис. 5.2 заряженным проводником. На больших расстояниях от проводника эквипотенциальные поверхности имеют характерную для точечного заряда форму сферы. По мере приближения к проводнику эквипотенциальные поверхности становятся все более сходными с поверхностью проводника, которая является эквипотенциальной. Вблизи выступов эквипотенциальные поверхности располагаются гуще, значит и, напряженность поля здесь больше. Отсюда следует, что плотность зарядов на выступах должна быть наибольшей. К такому же выводу можно прийти, учтя, что из–за взаимного отталкивания заряды стремятся расположиться как можно дальше друг от друга.
Покажем, что напряженность поля, созданного заряженным проводником вблизи его поверхности пропорциональна поверхностной плотности заряда. Выделим на поверхности Sпроводника площадку dS и построим на ней цилиндр с образующими, перпендикулярными к площадке dS, высотой dl.
На поверхности проводника вектор напряженности поля Поток вектора электрического смещения
С другой стороны, по теореме Остроградского-Гаусса:
гдеσ – поверхностная плотность зарядов на dS. Из равенства правых частей следует, что
Поверхностная плотность зарядов при данном потенциале проводника определяется кривизной поверхности – она растет с увеличением положительной кривизны (выпуклости) и убывает с увеличением отрицательной кривизны (вогнутости).
Поэтому вблизи углублений в проводнике эквипотенциальные поверхности расположены реже (рис. 5.3). Соответственно напряженность поля и плотность зарядов в этих местах будет меньше. На острие плотность заряда наибольшая, поэтому напряженность электростатического поля максимальна на острие заряженного проводника.
Так как на остриях велика плотность заряда, поэтому напряженность поля вблизи острия может быть настолько большой, что возникает ионизация молекул газа, окружающего проводник. Ионы иного знака, чем q, притягиваются к проводнику и нейтрализуют его заряд. Ионы того же знака, что и q, начинают двигаться от проводника, увлекая с собой нейтральные молекулы газа. В результате возникает ощутимое движение газа, называемое электрическим ветром. Заряд проводника уменьшается, он как бы стекает с острия и уносится ветром. Такое явление называют истечением заряда с острия (электростатический ветер). Большая напряженность поляEна остриях – нежелательное явление, т.к. происходит утечка зарядов и ионизация воздуха.Ионы уносят электрический заряд, проводник разряжается Есть наглядные эксперименты по этому явлению: сдувание пламени свечи электрическим ветром, колесо Франклина или вертушка, электростатический двигатель.
Таким образом, на заряженном проводнике заряды распределяются по его поверхности. Если заряженный металлический шарик привести в соприкосновение с поверхностью какого-либо проводника, то заряд шарика частично передается проводнику: шарик будет разряжаться до тех пор, пока их потенциалы не выровняются. Иначе обстоит дело, если шарик привести в соприкосновение с внутренней поверхностью полого проводника. При этом весь заряд с шарика стечет на проводник и распределится на внешней поверхности проводника (рисунок).
Потенциал полого проводника может быть больше, чем потенциал шарика, тем не менее, заряд с шарика стечет полностью. В точке 1 потенциал шарика меньше потенциала проводника (
Это свойство распределения зарядов по поверхности проводника можно использовать при перенесении заряда с одного проводника на другой или при создании электростатических генераторов.
|
|||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 202; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.192.3 (0.016 с.) |
 .
.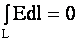 .
.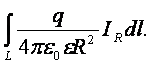
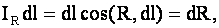 а
а 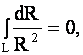 то
то 

 , отрицательные в противоположную сторону. В результате у концов проводника возникают заряды противоположного знака, называемые индуцированными зарядами (рис. 5.1).
, отрицательные в противоположную сторону. В результате у концов проводника возникают заряды противоположного знака, называемые индуцированными зарядами (рис. 5.1).
 это означает, что потенциал внутри проводника и на его поверхности должен быть постоянным (
это означает, что потенциал внутри проводника и на его поверхности должен быть постоянным ( )
)
 (2)
(2) , так как E = 0.
, так как E = 0.

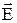 и вектор электрического смещения
и вектор электрического смещения  перпендикулярны поверхности. Поэтому поток
перпендикулярны поверхности. Поэтому поток 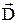 сквозь боковую поверхность равен нулю.
сквозь боковую поверхность равен нулю. через
через 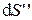 тоже равен нулю, так как
тоже равен нулю, так как  и, следовательно,
и, следовательно,  . Отсюда следует, что поток
. Отсюда следует, что поток  сквозь замкнутую поверхность равен потоку
сквозь замкнутую поверхность равен потоку  :
: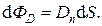

 , тогда
, тогда . (3)
. (3) Итак, напряженность поля вблизи поверхности заряженного проводника прямо пропорциональна поверхностной плотности зарядов.
Итак, напряженность поля вблизи поверхности заряженного проводника прямо пропорциональна поверхностной плотности зарядов.

 ),но пока мы переносили шарик в полость, мы совершили работу по преодолению сил отталкивания и, тем самым увеличивая потенциальную энергию, увеличили потенциал шарика. То есть, когда мы вносим шарик, потенциал его становится больше, и заряд как обычно перетекает от большего потенциала к меньшему. Перенося с помощью шарика следующую порцию заряда, мы совершаем еще большую работу. Это наглядный пример того, что потенциал – энергетическая характеристика.
),но пока мы переносили шарик в полость, мы совершили работу по преодолению сил отталкивания и, тем самым увеличивая потенциальную энергию, увеличили потенциал шарика. То есть, когда мы вносим шарик, потенциал его становится больше, и заряд как обычно перетекает от большего потенциала к меньшему. Перенося с помощью шарика следующую порцию заряда, мы совершаем еще большую работу. Это наглядный пример того, что потенциал – энергетическая характеристика.


