
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення моментів інерції твердих тіл з допомогою крутильного маятникаСодержание книги
Поиск на нашем сайте
Обладнання: стандартна лабораторна установка, масивне тверде тіло, мікрометр, штангенциркуль. Опис лабораторної установки Лабораторна установка містить в собі секундомір з пультом керування установкою (кнопки 1, 2, 3 та 4) і штатив, змонтовані на одному столику. На штативі на натягнутому дроті 8 підвішено рамку 7 з металевим вказівником 5 для запуску секундоміра з допомогою фотоелемента. Рамка починає коливання після вимикання електромагніту 6. Короткі теоретичні відомості Коливання крутильного маятника в повітрі із закріпленим у рамці масивним твердим тілом можна вважати гармонічними. За основним законом обертального руху, обертальний момент:
де Рівняння (20.1) можна також записати у вигляді:
Однорідне диференціальне рівняння другої степені (20.2) коливань крутильного маятника при величині
Знаючи період коливань крутильного маятника та користуючись рівнянням (20.3), можна визначити момент інерції цього маятника:
Запишемо відоме співвідношення між модулем зсуву
де Підставляючи (20.5) в (20.4), отримаємо:
Теоретичне значення для циліндра: для куба:
де Визначений за формулою (20.6) момент інерції ‑ це сумарний момент інерції рамки маятника і твердого тіла відносно осі маятника:
де Користуючись виразами (20.8) та (20.6) отримаємо:
де Порядок виконання роботи 1. Закріпіть досліджуване тіло вздовж його геометричної осі в рамці. 2. З дозволу викладача ввімкніть прилад в мережу та натисніть “Сеть”. 3. Поверніть рамку до її фіксації електромагнітом. 4. Натисніть клавіші “Сброс” та “Пуск”. 5. Після відліку лічильником чотирьох коливань (індикатор “Периоды“) натисніть клавішу “Стоп“. Мілісекундомір покаже час п'яти коливань. 6. Розділіть покази секундоміра на кількість коливань – це буде період коливань 7. Значення 8. Вийміть з рамки приладу досліджуване тіло. 9. Повторіть дії пп. 3‑8 для рамки без тіла в ній, в результаті чого знайдете період коливань 10. З допомогою штангенциркуля виміряйте діаметр
11. З допомогою штангенциркуля визначте довжину
12. Визначте момент інерції 13. Обчисліть теоретичне значення момента інерції
14. Результати вимірювань і обчислень занесіть до звітної таблиці 20.1. Таблиця 20.1
15. Обчисліть середнє арифметичне значення момента інерції тіла:
де 16. Обчисліть середньоквадратичне відхилення:
17. Розрахуйте абсолютну похибку:
де 18. Запишіть кінцевий результат:
19. Обчисліть відносну похибку розрахунку:
20. Розрахуйте відносно теоретичну похибку розрахунку:
21. Сформулюйте та запишіть висновок до роботи. Контрольні запитання до лабораторної роботи № 20 Поняття абсолютно твердого тіла, закон руху його центра мас. Момент сили і момент інерції твердого тіла відносно нерухомої осі. Основний закон обертального руху твердого тіла. Кінетична енергія тіла, яке обертається відносно нерухомої осі. Обчислення похибок при непрямих вимірюваннях. Лабораторна робота №21
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 267; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 Мета роботи: визначити момент інерції твердого тіла відносно деякої осі обертання.
Мета роботи: визначити момент інерції твердого тіла відносно деякої осі обертання.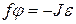 , (20.1)
, (20.1) ‑ константа момента пружних сил;
‑ константа момента пружних сил;  ‑ момент інерції твердого тіла;
‑ момент інерції твердого тіла;  ‑ кутове прискорення (відносно осі обертання).
‑ кутове прискорення (відносно осі обертання). (20.2)
(20.2) має коефіцієнт,
має коефіцієнт, 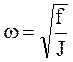 що дорівнює циклічній частоті
що дорівнює циклічній частоті 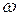 коливань маятника. Оскільки
коливань маятника. Оскільки  , то для періоду
, то для періоду  коливань крутильного маятника можемо записати:
коливань крутильного маятника можемо записати: (20.3)
(20.3) (20.4)
(20.4) і константою момента пружних сил
і константою момента пружних сил  , (20.5)
, (20.5) ‑ радіус дроту;
‑ радіус дроту;  - довжина дроту в крутильному маятнику.
- довжина дроту в крутильному маятнику. (20.6)
(20.6) для тіла відносно осі його обертання, що є віссю його симетрії:
для тіла відносно осі його обертання, що є віссю його симетрії:
 , (20.7)
, (20.7) ‑ радіус основи циліндра,
‑ радіус основи циліндра,  ‑ довжина ребра куба,
‑ довжина ребра куба,  ‑ маса тіла.
‑ маса тіла. , (20.8)
, (20.8) та
та  ‑ моменти інерції відповідно для твердого тіла та рамки маятника.
‑ моменти інерції відповідно для твердого тіла та рамки маятника. , (20.9)
, (20.9) та
та  ‑ періоди коливань маятника без досліджуваного тіла та з ним.
‑ періоди коливань маятника без досліджуваного тіла та з ним. дроту маятника та розрахуйте його радіус
дроту маятника та розрахуйте його радіус  досліджуваного тіла за формулою (20.9) і згідно з табл. Д2.
досліджуваного тіла за формулою (20.9) і згідно з табл. Д2. , кг·м2
, кг·м2
 , кг2·м4
, кг2·м4
 , (20.10)
, (20.10) ‑ кількість значень.
‑ кількість значень. (20.11)
(20.11)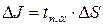 , (20.12)
, (20.12)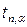 ‑ коефіцієнт Стьюдента.
‑ коефіцієнт Стьюдента. (20.13)
(20.13)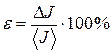 (20.14)
(20.14)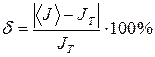 (20.15)
(20.15)


