
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналітичний спосіб визначення параметрів лінійної залежностіСодержание книги
Поиск на нашем сайте
Іншим способом визначення параметрів лінійної залежності, отриманої експериментальним шляхом, є аналітичний, який відомий також як метод найменших квадратів, ідея якого полягає в тому, що серед можливих комплектів пар чисел
де Виконавши розрахунки за формулами (ІІ.34) та (ІІ.35), бажано виконати перевірку: для цього потрібно за виразом (ІІ.27) визначити ординати прямої лінії при двох довільних значеннях абсциси Похибки розрахунку значень
де Правила округлень в розрахунках Поняття «оцінка похибки», крім всього іншого, також вказує на той факт, що немає сенсу вести розрахунки з «великою точністю», тобто, якщо при розрахунку отрималося деяке числове значення з великою кількістю цифр, то всі їх переписувати непотрібно. Для того, щоб правильно записати отриманий розрахунковий результат необхідно визначити лише першу значущу цифру, оскільки знання похибки, власне, й потрібне для того, щоб знайти той граничний розряд результату вимірювання, в якому міститься похибка. Цифри в розрядах, старших від граничного є достовірними, а в розрядах нижчих граничного – недостовірними. Цифра граничного розряду займає проміжне положення між достовірними і недостовірними розрядами та є частково достовірною, а її достовірність як раз і задається першою значущою цифрою похибки. В якості першої значущої цифри слід завжди приймати першу відмінну від нуля цифру в записі числа. Виходячи з вищесказаного, можемо сформулювати наступне правило округлень: похибку потрібно заокруглювати до однієї значущої цифри, а результат вимірювань – до граничного розряду. Так, наприклад, якщо при визначенні густини деякої речовини було отримано значення
Граничним розрядом у наведеному прикладі буде розряд десятків, а цифрою граничного розряду є цифра «7». Цифра «8» є достовірною, цифри «7» та «3» є частково достовірними, а цифри «0» є недостовірними. Щоб уникнути запису в кінцевому результаті недостовірних цифр можна використовувати науковий формат запису результату вимірювань, що передбачає запис отриманого результату з використанням мантиси та показника степені. Нехай в результаті розрахунку було отримане деяке число
де Отже, отриманий раніше результат
Для більш компактного запису отриманого результату рекомендується використовувати префікси десяткових одиниць (табл. Д4), у такому випадку останній запис може мати вигляд:
В ході проведення розрахунків рекомендується, якщо це можливо, вести запис проміжних результатів з кількістю цифр, що хоча б на одну цифру буде довшою від запису кінцевого результату. Тобто, якщо в кінцевому результаті очікується запис числа з округленням до сотих, то проміжні розрахунки бажано заокруглювати з точністю до тисячних – це дасть можливість попередити появу великої похибки в кінці вимірювань. ДОДАТКИ Додаток 1 Якісні задачі 1. Вагонетка, завантажена рудою, рухається з прискоренням 2. Які з наведених рівнянь: 1)
4. Накресліть графіки залежності швидкості та шляху деяких тіл від часу, маючи графіки прискорень цих тіл (рис. Д1.1). Початкова швидкість тіл у всіх випадках дорівнює нулю. 5. Кулька вільно падає на горизонтальну плиту з висоти
7. Велосипедист робить «вісімку» (рис. Д1.2). Як змінюється його прискорення під час цього руху? 8. Через нерухомий блок, вісь якого горизонтальна, перекинуто мотузку довжиною 9. Три тіла кинуті так: перше – вниз без початкової швидкості, друге – вниз з початковою швидкістю, третє – вгору. Що можна сказати про прискорення цих тіл? Опором повітря знехтуйте. 10. Забити цвях у фанерну стінку важко – при ударі фанера прогинається. Однак цвях вдається забити, якщо з протилежного боку стінку підперти масивним тілом. Як це можна пояснити? 11. Чому навантажений 50-тонний вагон, причеплений до пасажирського потягу, робить хід потягу більш плавним? 12. Чому небезпечно ривками піднімати шахтну кліть?
14. Чи можуть одночасно рухатися частини установки, зображеної на рис. Д1.3, за напрямами, що вказано стрілками?
16. На рис. Д1.4 показано залежність сили тертя в рідині від швидкості руху тіла. Чому дорівнює сила тертя, коли тіло знаходиться в стані спокою відносно рідини? Який фізичний зміст такої форми кривої графіка? 17. Правила технічної експлуатації залізниць вимагають, щоб двері критих вантажних вагонів, що їдуть порожніми, були закриті. Чому? 18. Чому кулька в циліндричній трубці, що наповнена в’язкою рідиною, падає з прискоренням, яке поступово зменшується, а при достатній довжині трубки рух кульки надалі стає рівномірним? 19. Якщо одночасно відпустити монету і такої ж величини паперовий круг, то вони будуть падати з різною швидкістю. Якщо ж цей круг покласти на монету і відпустити з монетою, то вони впадуть разом. Поясніть це явище. 20. Після сильного шторму вода в морі стає теплішою. Чому? 21. Як рухаються кабіни в атракціоні «Колесо огляду»: поступально чи обертально? 22. На потяг, що рухається прямолінійно вздовж горизонтальної ділянки шляху, діє постійна сила тяги тепловоза, рівна силі тертя. Який рух здійснює поїзд? Як проявляється в даному випадку закон інерції?
24. Насоси перекачують воду з нижнього рівня каналу в камеру шлюзу для підйому суден на більш високий рівень. Чи однакову роботу виконують насоси, коли в камері спочатку знаходиться великий теплохід, а потім – маленький човен? 25. Чи зміниться величина роботи, що виконується двигуном ескалатора, якщо пасажир, який стоїть на сходах ескалатора, що рухаються вгору, буде підійматися по сходах з постійною швидкістю? 26. У довгій посудині з теплоізольованими стінками знаходиться газ. Посудина закрита теплоізольованим поршнем. Поршню миттєво надається постійна швидкість. Як змінюється температура газу? Як залежить зміна температури газу від швидкості поршня? 27. Нагрівається чи охолоджується ідеальний газ при розширенні, якщо його тиск 28. Чому іній на деревах зникає іноді без відлиги? 29. Крапля води, потрапивши на розжарену плиту, починає на ній стрибати. Чому? 30. Чи впливає вітер на покази термометра? 31. Чому багато речей, висихаючи, коробляться (деформуються)? 32. Як змінюється абсолютна і відносна вологість повітря при його нагріванні? 33. Чи однаковий тиск водяної пари в закупореній посудині з водою і в атмосфері під час туману, якщо температура повітря в обох випадках однакова? 34. Чому сильна спека важче переноситься людиною в болотистих місцях, ніж у сухих? 35. Яку рідину можна налити в склянку вище країв? Чому? 36. Чому погано витираються мокрі руки вовняною або шовковою тканинами? 37. Якщо покласти шматок крейди на мокру губку, він намокне. Якщо суху губку покласти на мокру крейду, вона залишиться сухою. Чому? 38. а) як пояснити, що вода, яка знаходиться в слабо обпаленій глиняній посудині з дрібними порами, має температуру нижчу, ніж температура навколишнього повітря. б) за яких умов температура води в цій посудині буде такою ж, як і температура навколишнього середовища? 39. Чому балони зі стислим повітрям вибухонебезпечні, а труба з водою під великим тиском – вибухобезпечна? 40. Чому, спускаючись на човні по річці, пливуть посередині річки, а підіймаючись – намагаються триматися берега? 41. Що важче: 1 кг заліза, чи 1 кг вати? А в вакуумі? 42. Як і в якому напрямі потрібно стрибати з рухомого автомобіля, щоб якомога менше забитися? 43. Чому після сильного снігопаду стає значно тихіше? 44. Чому при виконанні повороту автомобілем небезпечно натискати на гальма і чому тиснуть на гальма гонщики при виході з повороту? 45. Чи відрізняється і чому тиск в середині мильної бульбашки від зовнішнього атмосферного тиску? Додаток 2 Таблиця Д2 Додаткові дані до лабораторних робіт
При необхідності дані, що їх наведено в табл. Д2, дозволяється редагувати «від руки» та/чи доповнювати ними відповідні комірки таблиці. Додаток 3 Таблиця Д3 Фізичні константи
Додаток 4 Таблиця Д4 Множники і префікси утворення десяткових кратних одиниць
Додаток 5 Таблиця Д5 Основні одиниці СІ
При виконанні обчислень шуканих величин необхідно слідкувати за розмірністю тих даних, які використовуються в розрахунках та вказувати розмірність кінцевого результату. Щоб упевнитися в надійності розрахунків бажано виконувати перевірку розмірності результату, яка включає в себе виконання арифметичних операцій з одиницями вимірювання: 1) додавати/віднімати можна лише однакові розмірності – в результаті отримаємо ту ж таки розмірність (наприклад, см + см = см); 2) дії множення/ділення, піднесення в степінь тощо для розмінностей виконуються як зі звичайними числами (наприклад, см/с∙кг/см=кг/с) Приклад: нехай шуканою величиною є момент інерції деякого твердого тіла, що визначається за формулою
Додаток 6 Таблиця Д6 Визначення похибок функцій однієї змінної
* ‑ для досить великих значень ** ‑ Додаток 7 Таблиця Д7 Визначення похибок функцій кількох змінних
Додаток 8 Таблиця Д8 Психрометрична таблиця
Таблиця містить значення максимальної вологості повітря (в мм.рт.ст.) при його різних температурах. Перший стовпчик відповідає цілій, а перший рядок ‑ дробовій частинам показів термометра. Так, якщо на термометрі 18,5°, то максимальна вологість повітря рівна 15,97 мм.рт.ст – навпроти «18» по першому стовпчику та під «0,5» по першому рядку. Додаток 9 Таблиця Д9 Коефіцієнти Стьюдента
Додаток 10 Виконання вимірювань штангенциркулем Для вимірювання довжин та/чи відстаней з точністю порядку 1 мм використовують лінійку (масштаб) з довжиною поділки (яку називають ціною поділки) 1 мм. Підвищити точність вимірювань можна, доповнивши масштаб ноніусом.
Лінійний ноніус – це невелика лінійка, що ковзає вздовж масштабу («основної лінійки»). На цій лінійці міститься маленька шкала, що має | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 та
та  існує єдиний такий комплект, для якого сума квадратів відхилень ординат експериментальних точок від відповідних ординат прямої лінії з параметрами
існує єдиний такий комплект, для якого сума квадратів відхилень ординат експериментальних точок від відповідних ординат прямої лінії з параметрами  (ІІ.34)
(ІІ.34) , (ІІ.35)
, (ІІ.35) ‑ число експериментальних точок;
‑ число експериментальних точок;  та
та  ‑ абсциса та ордината деякої
‑ абсциса та ордината деякої  -ої експериментальної точки;
-ої експериментальної точки;  ;
;  ;
;  ;
;  ;
;  .
. , нанести на графіку ці дві точки та сполучити їх прямою лінією, котра, якщо все було виконано правильно, автоматично має пройти через всі довірчі інтервали експериментальних точок і буде максимально наближеною до них.
, нанести на графіку ці дві точки та сполучити їх прямою лінією, котра, якщо все було виконано правильно, автоматично має пройти через всі довірчі інтервали експериментальних точок і буде максимально наближеною до них. (ІІ.36)
(ІІ.36) , (ІІ.37)
, (ІІ.37) ;
;  .
. =856,72 кг/м3, а оцінка похибки дала результат
=856,72 кг/м3, а оцінка похибки дала результат 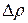 =31,289 кг/м3, то кінцевий запис
=31,289 кг/м3, то кінцевий запис  =(856,72±31,289) кг/м3 буде неправильним! В даному випадку першою значущою цифрою похибки буде цифра «3», тому кінцевий результат потрібно записати в такому вигляді:
=(856,72±31,289) кг/м3 буде неправильним! В даному випадку першою значущою цифрою похибки буде цифра «3», тому кінцевий результат потрібно записати в такому вигляді: . Науковим форматом запису цього числа буде наступний:
. Науковим форматом запису цього числа буде наступний: , (ІІ.37)
, (ІІ.37) ‑ мантиса числа (бажано дотримуватися правила
‑ мантиса числа (бажано дотримуватися правила  );
);  ‑ порядок числа.
‑ порядок числа. (
( ). Відомо, що в кінці четвертої секунди швидкість вагонетки дорівнює 6 м/с. Що можна сказати про величину шляху, пройденого за четверту секунду? Буде цей шлях більше, менше чи дорівнюватиме 6 м?
). Відомо, що в кінці четвертої секунди швидкість вагонетки дорівнює 6 м/с. Що можна сказати про величину шляху, пройденого за четверту секунду? Буде цей шлях більше, менше чи дорівнюватиме 6 м? , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  , 5)
, 5)  описують рівномірний рух?
описують рівномірний рух? 3. Рівняння швидкості тіла, що рухається, має вигляд:
3. Рівняння швидкості тіла, що рухається, має вигляд:  . Яке його рівняння шляху?
. Яке його рівняння шляху? . Вважаючи удар абсолютно пружним, накресліть графіки залежності швидкості кульки і її висоти над плитою від часу Часом удару знехтувати.
. Вважаючи удар абсолютно пружним, накресліть графіки залежності швидкості кульки і її висоти над плитою від часу Часом удару знехтувати.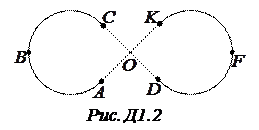 6. Через нерухомий блок перекинуто мотузку. Один кінець мотузки тримає людину, а до іншого прикріплений вантаж. Маса вантажу дорівнює масі людини. Що відбудеться, якщо людина почне на руках підтягуватися вгору по мотузці? Відповідь поясніть.
6. Через нерухомий блок перекинуто мотузку. Один кінець мотузки тримає людину, а до іншого прикріплений вантаж. Маса вантажу дорівнює масі людини. Що відбудеться, якщо людина почне на руках підтягуватися вгору по мотузці? Відповідь поясніть. . За кінці мотузки тримаються дві людини, що знаходяться на однакових відстанях
. За кінці мотузки тримаються дві людини, що знаходяться на однакових відстанях  від блока. Обидві людини починають одночасно підніматися вгору, причому одна з них піднімається відносно мотузки зі швидкістю
від блока. Обидві людини починають одночасно підніматися вгору, причому одна з них піднімається відносно мотузки зі швидкістю  , а інша – зі швидкістю
, а інша – зі швидкістю  . Порівняйте час, через який кожна людина досягає блока? Масою блока і мотузки знехтувати; маси людей однакові.
. Порівняйте час, через який кожна людина досягає блока? Масою блока і мотузки знехтувати; маси людей однакові. 13. Чому верхні спиці колеса, що котиться, іноді зливаються для очей, в той час як нижні видно роздільно?
13. Чому верхні спиці колеса, що котиться, іноді зливаються для очей, в той час як нижні видно роздільно?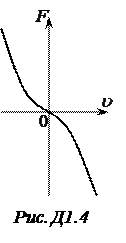 15. Чому дуже легке тіло важко кинути на далеку відстань?
15. Чому дуже легке тіло важко кинути на далеку відстань? 23. На рис. Д1.5 подано графік швидкості рухомого тіла. Що можна сказати про сили, що діють на це тіло?
23. На рис. Д1.5 подано графік швидкості рухомого тіла. Що можна сказати про сили, що діють на це тіло?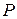 і об’єм
і об’єм 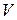 зв’язані формулою
зв’язані формулою  , де
, де  ? Маса газу залишається постійною.
? Маса газу залишається постійною.








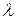


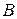















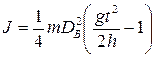 , виконаємо перевірку розмірності (в якості одиниць вимірювання величин слід приймати ті, з якими ці величини будуть підставлятися в розрахункову формулу):
, виконаємо перевірку розмірності (в якості одиниць вимірювання величин слід приймати ті, з якими ці величини будуть підставлятися в розрахункову формулу): ‑ розмірність правильна.
‑ розмірність правильна.





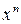






 *
*


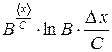



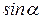
 **
**
 **
**
 **
**
 **
**

 **
**
 **
**

 **
**
 **
**
 (
(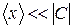 )
) вимірюється в радіанах
вимірюється в радіанах










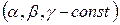





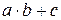





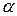


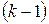 поділок основного масштабу, тобто:
поділок основного масштабу, тобто:


