
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Центробежный регулятор (центробежный маятник)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Рассмотрим силы, действующие на муфту регулятора скорости. К муфте приложены две приведенные силы: 1) упругая или поддерживающая сила 2) регулирующая (приведенная центробежная)сила Изобразим зависимости При установившемся движении, которому соответствует координата z 0 (точка А на рис. 1), регулятор находится в равновесии:
Рисунок 1 Силы действующие на муфту регулятора скорости
Предположим, мы имеем дело с малым возмущением силового поля, а следовательно, с малыми колебаниями муфты около положения равновесия:
Обозначим массу, приведенную к муфте, через М, тогда движение регулятора описывается дифференциальным уравнением
Далее обозначим:
Вычтем (1) из (2), получим уравнение малых колебаний регулятора
Так как
то уравнение регулятора принимает вид:
Для улучшения процесса регулирования в некоторых схемах вводят демпферы, называемыми катарактами (рис. 2), у которых степень демпфирования изменяются с помощью дросселя (перекрытие канала 3).
Рисунок 2 Катаракт:
1 – поршень; 2 – цилиндр; 3 – зазор; 4 – дроссель; 5 – масло.
Вследствие действия катаракты на муфту регулятора, возникает сила демпфирования:
где
Введем относительные переменные:
где
Тогда (4) примет вид:
или
где
где
Если нет катаракты, то есть демпфирование отсутствует, то уравнение регулятора из–за
Такое уравнение описывает гармонические колебания. Для увеличения быстродействия регулятора необходимо увеличивать частоту собственных колебаний, то есть, чтобы можно было пренебречь его массой. А это требует Касательные и кориолисовы силы инерции При выводе (5) не учитывались касательные и кориолисовы силы, действующие на центробежный регулятор. Касательные силы инерции определяются как:
где
В коническом регуляторе эта сила направлена перпендикулярно к плоскости, проходящей через ось регулятора и центр тяжести груза и вызывает лишь трение в шарнирах, пропорциональное ускорению Кориолисова сила инерции, после начала движения муфты, вызывает тангенциальное движение в шарнирах и изменяется пропорционально изменению величины скорости относительного движения грузов, то есть влияния этой силы на движение регулятора будет такое же, как катаракта. Величина кориолисовой силы инерции:
где
Примем
где Тангенциальные и кориолисовы силы вызывают давление в шарнирах, что в свою очередь приводит к трению и появлению зоны нечувствительности. С учетом силы
Здесь ЛЕКЦИЯ №12
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 712; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

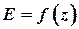 ;
; .
. .
.

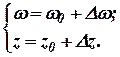
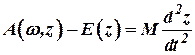 ,
,

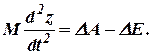
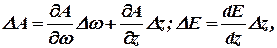
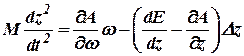 .
.


 – коэффициент пропорциональности, учитывающий передаточное число от приложения силы катаракта к муфте. Знак минус указывает, что сила катаракты всегда направлена в сторону, противоположную движению муфты. С учетом силы
– коэффициент пропорциональности, учитывающий передаточное число от приложения силы катаракта к муфте. Знак минус указывает, что сила катаракты всегда направлена в сторону, противоположную движению муфты. С учетом силы  уравнение регулятора примет вид:
уравнение регулятора примет вид: .
.

 – максимальный рабочий ход муфты, соответствующий максимальному статическому изменению регулируемой величины;
– максимальный рабочий ход муфты, соответствующий максимальному статическому изменению регулируемой величины;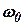 – значение регулируемой величины при режиме, который подвергается исследованию.
– значение регулируемой величины при режиме, который подвергается исследованию.




 – время катаракты;
– время катаракты;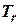 – время регулятора.
– время регулятора. с учетом постоянной скорости вращения
с учетом постоянной скорости вращения  станет таким:
станет таким: .
.
 , что достигается путем проектирования регулятора с малой приведенной массой и большой поддерживающей (силой упругости) силы.
, что достигается путем проектирования регулятора с малой приведенной массой и большой поддерживающей (силой упругости) силы.
 , (6)
, (6) – масса груза регулятора;
– масса груза регулятора; – радиус от силы вращения;
– радиус от силы вращения;
 – передаточное число между валом машины и валом регулятора (для упрощения принимаем
– передаточное число между валом машины и валом регулятора (для упрощения принимаем  );
);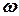 – угловая скорость вала турбины;
– угловая скорость вала турбины;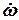 – ускорение вала турбины.
– ускорение вала турбины. . Эта сила имеет направление с изменением направления движения муфты регулятора.
. Эта сила имеет направление с изменением направления движения муфты регулятора. ,
,
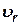 – относительная скорость движения грузов в плоскости, проходящей через ось регулятора;
– относительная скорость движения грузов в плоскости, проходящей через ось регулятора; – угол между вектором υr и этой осью.
– угол между вектором υr и этой осью.
 – коэффициент, представляющий передаточное число между ходом муфты и ходом грузов регулятора.
– коэффициент, представляющий передаточное число между ходом муфты и ходом грузов регулятора.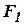 и
и  уравнение регулятора запишется:
уравнение регулятора запишется: .
.
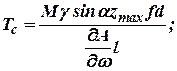

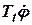 – отражает влияние касательных сил инерции.
– отражает влияние касательных сил инерции.


