Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие сведения о колебаниях. . 9Содержание книги
Поиск на нашем сайте
ВВЕДЕНИЕ.. 6 ОБЩИЕ СВЕДЕНИЯ О КОЛЕБАНИЯХ.. 9 Параметрические колебания. 9 Вынужденные колебания линейной системы с одной степенью свободы. 22 Колебания трубопроводов под лействием ветровой нагрузки. 33 ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ ПРЯМЫХ СТЕРЖНЕЙ.. 39 Основные допущения и уравнение поперечных колебаний прямого стержня 39 Краевые и начальные условия. 41 Собственные формы колебаний стержня и функции, их определяющие 43 ДИНАМИЧЕСКИЙ АНАЛИЗ ТРУБОПРОВОДОВ.. 46 Особенности динамического анализа. 46 Влияние расстояния между опорами трубопровода на его динамические характеристики. 50 Влияние типа опоры трубопровода на его динамические характеристики. 55 Влияние пружинных опор трубопровода на его динамические характеристики. 62 Влияние сосредоточенных масс на динамические характеристики трубопровода. 67 Динамический анализ обвязки насосного агрегата. 70 ЗАКЛЮЧЕНИЕ.. 78 СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ... 80
ВВЕДЕНИЕ Россия является одним из лидеров в мировой экономике по объемам добычи углеводородного сырья. Территория распределиния этих ресурсов весьма широка. Основная часть нефти и газа добывается в удаленных районах Сибири и Дальнего Востока. Главные же потребители – нефте- и газоперерабатывающие заводы преимущественно сосредоточены в центральной части России. Также, наша страна выступает одним из крупнейших экспортеров углеводородов в мире. Данные условия требуют транспортировки сырья на значительные расстояния. Наилучшим способом транспортировки является трубопроводный транспорт, так как он обладает рядом преимуществ перед другими способами транспортировки: - прокладка на любые расстояния и направления вне зависимости от ландшафта; - независимость от внешних условий (состояния погоды, времени года и суток); - высокая степень автоматизации; - отсутствие холостого пробега, который имеется при всех других видах транспорта, который возвращается обратно порожним. Что же касается нефтеперабатывающих производств, то кроме трубопроводного транспорта другие не представляются возможными, так как обычный транспорт не смог бы обеспечить непрерывность технологического процесса. Технологичекие трубопроводы объединяют большое количество производственного оборудования завода, ввиду чего, имеют сложную пространственную конфигурацию. Также данные трубопроводы испытывают значительный спектр нагрузок, которые действуют на магистральные трубопроводы в значительно меньшей степени или отсутствуют вовсе. Примерами таких нагрузок могут служить: - значительные температурные деформации, так как переработка нефти проиисходит при очень высоких температурах; - наличие большого количества арматуры и приборов КИПиА, являющихся источниками дополнительных концентраций напряжения; - преимущественно надземная прокладка трубопроводов, оказывающая напряжения при прогибе трубопроводов и возникающие ветровые нагрузки; - непосредственная близость расположения от технологического оборудования. Особенно это сказывается при работе динамических машин: насосов, компрессоров, АВО и т.д. Ввиду вышесказанного, становится важно какой важной задачей является корректный расчет технологических трубопроводов на воздейчтвие не только статических, но и динамических нагрузок Во время эксплуатации трубопроводов, содержащих пульсирующие потоки рабочей среды, возникает нарушение его герметичности и поломка арматуры, выводят из строя средства контроля и автоматики, оказывается неблагоприятное воздействие на обслуживающий персонал, даже в тех случаях, когда и нет непосредственной опасности для трубопроводов, аппаратов и строительных конструкций. Данные колебания опасны тем, что при определенных соотношениях частот вынужденных и собственных колебаний трубопровода возникает явление, называемое параметрическим резонансом, проявляющееся в неограниченном возрастании амплитуды параметрических колебаний. При проявлении резонанса трубопровод становится подвержен циклическому воздействию, который может стать причиной разрушения от усталостных напряжений. Таким образом, главной задачей динамического расчета конструкции, подверженной параметрическим колебаниям, является определение значений частот, при которых возможно проявление параметрического резонанса. Эти знания позволяют принять на стадии проектирования меры для избежания попадания конструкции во время эксплуатации в данные границы значений. ОБЩИЕ СВЕДЕНИЯ О КОЛЕБАНИЯХ Параметрические колебания Важным ампектом увеличения срока службы трубопровода является минимизация или полное устранение нежелательных вибраций, которые приводят к повреждению изоляции, коррозионному растрескиванию, усталостным напряжениям в стенке трубы. При неблагоприятных стечениях обстоятельств воздейчтвие вираций может привести даже к разрушению трубопровода. Спектр колебаний трубопровода представляет собой сложный комплекс взаимодействия свободных, вынужденных, параметрических, автоколебательных процессов. Спектр собственных частот конструкции очень широк. Значения собственных частот зависят от параметров самой системы и не зависят от внешних нагрузок. Примерами таких параметров могут служить: условия закрепления концов, ограничения перемещениям трубы, возникающих продольных сил, скорости и объемов движения жидкости, ее пульсации, упругих свойств грунта. Поэтому высока вероятность резонансных явлений при совпадении вынужденных и собственных частот при основном силовом резонансе или возникновения параметрических резонансов. Остановимся подробнее на параметрических колебаниях. По внешним проявлениям параметрические колебания очень схожи с обычными вынужденными, ввиду чего, они могут ошибочно классифицироваться как обычные резонансные. На самом же деле пареметрические колебания имеют принципиальные отличия. Параметрические колебания поддерживаются за счет изменения параметров системы. При определенных сочетаниях между частотой возмущающей силы и собственными частотами системы малое начальное возмущение приводит к развитию колебаний большой амплитуды. Соотношение частот, при котором наступает параметрический резонанс, отличается от соотношения частот при вынужденных колебаниях. Обычный резонанс – это возрастающие вынужденные колебания устойчивой системы, возникающие под действием возмущающей силы. Он проявляется только тогда, когда частота возмущающей силы равняется частоте собственных колебаний системы. Параметрический резонанс представляет собой возрастающие колебания около неустойчивого положения равновесия, т.е. параметрический резонанс связан с неустойчивостью равновесного состояния системы, при котором любое случайное возмущение приводит к её раскачке. Так, например, главный параметрический резонанс может быть реализован при амплитуде продольной силы составляющей менее одного процента от эйлерового значения. Для параметрического резонанса характерно наличие сплошных областей возбуждения (областей динамической неустойчивости). При обычном резонансе амплитуда колебаний возрастает по линейному, а при параметрическом – по экспоненциальному закону. Поэтому параметрический резонанс является наиболее опасным явлением. Параметрические колебания характеризуются еще одной особенностью. Если при обычном резонансе введение трения пропорционально скорости приводит к ограничению амплитуды колебаний, то параметрический резонанс может развиваться и при наличии трения. Вне области неустойчивости установившиеся колебания происходят с частотой внешней нагрузки. Магистральные трубопроводы выделяются своей большой протяженностью, разнообразием условий эксплуатации, значительными величинами диаметров и масс. Прокладка различных участков может быть осуществлена наземным, надземным, подводным и подземным способом. При подземной прокладке грунт оказывает большое демпфирующее воздействие. Возмущающие нагрузки могут быть различного происхождения: механического, гидродинамического, акустического происхождения, а также быть связанным с изменением температурного поля и сейсмическим воздействием. При надземной прокладке трубопроводы изгибаются под собственным весом и под действием переменного внутреннего давления совершают пространственные колебания. Значения амплитуды колебаний могут изменяться при различных соотношениях внешних нагрузок. Рассматриваются пространственные колебания трубы и заключенной в ней жидкости относительно горизонтальной оси, проходящей через опоры. В статическом состоянии труба изогнута собственным весом и находится под действием внутреннего давления. Предполагается, что она выводится из этого состояния путем отклонения на угол θ от вертикальной плоскости. Коэффициент упругости опор и деформации трубы, связанные с ее выходом из плоскости изгиба, считаются малыми, поэтому изогнутая ось трубопровода является плоской кривой. При этом учитываются силы инерции Кориолиса, выталкивающая сила Архимеда и сила сопротивления, пропорциональная первой степени скорости. Колебания трубы происходят под действием переменного внутреннего давления. Длина трубы равна L, толщина ее стенки – h, а суммарная масса однородной трубы и жидкости – m. Слева на рис. 1.1 изображен элемент трубы длиной dx и массой dm =(m/L) * dx, а справа на этом же рисунке показаны ускорения и силы, действующие на выделенный элемент трубы. Рисунок 1.1 - Расчетная схема изгибно-вращательных колебаний трубопровода.
Анализ последствий ряда землетрясений выявил, что под воздействием сейсмических нагрузок стальные магистральне трубопроводы очень часто получают повреждения различного рода вплоть до их разрушения. Во время исследования работы газопроводов, работающих в зонах гидродинамической активности, были получены следующие результаты. Вынужденные колебания возникают из-за действия многих аппаратов, одновременно работающих в сети. Примерами таких трубопроводов является трубопровод, сообщающийся с двумя и более резервуарами, на поверхности которых возникают волны различных типов с разными частотами. Типы волн давления показаны на рис. 1.2. Насосы могут вызвать вынужденные колебания на линии нагнетания, действующие на низовой трубопровод, а линии всасывания – вынужденные колебания, действующие на верховой трубопровод. Если на трубопроводе установлен байпас, то на него будут действовать два вынужденных колебания. Анализируя количество аварий, становится ясно, что около 2/3 от общего числа отказов происходят вблизи компрессорных станций, на участке до 15км..
Рисунок 1.2 - Типы волн, возникающих в трубопроводах.
Примерно такой же участок трубопровода (до 20 км от насосных агрегатов) считают динамически активным специалисты, занимающиеся вопросами отказа трубопроводов по причине коррозионного растрескивания под напряжением. Причем в зависимости от конкретных условий эксплуатации разрушение трубопроводов из-за коррозионного растрескивания под напряжением начинает проявляться через 5-16 лет после пуска их в эксплуатацию. С помощью высокочувствительных микросейсмических съемок вдоль трасс магистральных газопроводов установлены участки с повышенными показателями вибраций технологического характера. Компрессорные станции, являющиеся мощными источниками вибраций, способствуют образованию в системе "труба-грунт" колебаний от долей до сотен герц. Уровень микросейсмических шумов у компрессорных станций на два порядка превышает уровень шумов на участках, удаленных от компрессорных станций на более чем 15 км. Выявлена способность слабых вибраций с амплитудой 10 100 мкм/с в диапазоне частот 10- 40 Гц в системе "грунт-труба" повышать уровень технологических вибраций, отрицательно влияющих на техническое состояние трубопровода. Вышеизложенные результаты согласуются с современными представлениями о возникновении параметрических резонансов. На основании анализа опубликованных работ на рис. 1.3 представлены некоторые причины возникновения низкочастотных колебаний трубопроводов. Рассмотрим возможность устранения параметрического резонанса от действия продольной силы с пульсирующей составляющей. Это может быть достигнуто за счет снижения глубины пульсации и изменении упруго-диссипативной характеристики трубопровода. Параметрические колебания в детерминированных системах при линейной и нелинейной постановке задач исследованы весьма подробно. Рисунок 1.3 - Некоторые причины низкочастотных колебаний трубопровода Дифференциальное уравнение для определения динамического прогиба трубопровода при действии продольной силы с пульсирующей составляющей имеет вид:
где P 0 – постоянная составляющая продольной силы; P 1 – амплитуда переменной составляющей продольной силы; ω – возмущающая частота; EJ – жесткость трубопровода на изгиб; m – масса единицы длины трубопровода. Граничным условием шарнирно опертого участка трубопровода удовлетворяет функция
где T (t) – неизвестная функция времени; l – длина рассматриваемого участка трубопровода. При подстановке выражения (1.2) в уравнение (1.1) для n = 1, получим . Поскольку sin (πx/l) ≠0, из условия (3) имеем:
где Обозначив
придем к уравнению Матье
Уравнение Матье хорошо изучено и используется для оценки динамической устойчивости механических систем, подверженных параметрическим колебаниям. В параметрах a и q (1.5) строят диаграмму устойчивости Айнса-Стрейта (см. рис. 1.4). Неустойчивые области заштрихованы. Так, например, точка A находится в зоне параметрического резонанса, а точка N – в зоне устойчивых колебаний. Рисунок 1.4 - Диаграмма Айнса-Стретта с тремя областями резонанса
Показанные на диаграмме устойчивости три резонанса являются наиболее опасными при параметрических колебаниях, особенно первый при a =1, когда ω =2 ω 0, где ω – частота возбуждения, ω 0 – частота собственных колебаний механической системы. Оценим свойства параметрических колебаний при изменении частоты возбуждения ω. Как показывают выражения (1.5) с увеличением частоты возбуждения ω (рис. 2) параметры a и q будут уменьшаться по прямой, приближающейся к началу координат с угловым коэффициентом
Линия 1 (см. рис. 1.4) при этом пересекает чередующиеся области устойчивости и неустойчивости. В областях неустойчивости возникает параметрический резонанс. С увеличением глубины пульсации q за счет роста углового коэффициента K линия 2 пересекает области неустойчивости с большими интервалами и зоны параметрического резонанса расширяются. Уменьшая коэффициент K можно снизить величину интервалов резонансных зон. Это достигается (см. выражение 1.7) путем снижения величины составляющей продольной силы P 0, пульсирующей составляющей P 1, повышением величины критической силы Pкр. В качестве примера на диаграмме Айнса-Стретта (см. рис. 1.5) показаны области динамической неустойчивости трубопровода диаметром 402 мм с толщиной стенки 15 мм при разных длинах участков. Если для трубопровода при l =150 м и l =200 м (линии 1 и 2) неустойчивость наступает вблизи значений a =1 и a =4, то с увеличением длины l и глубины пульсации (линии 3 и 4) возрастают интервалы динамической неустойчивости. Рисунок 1.5. Фрагмент диаграммы Айнса-Стреттас главным и вторым параметрическими резонансами
Амплитуды колебаний быстро убывают с увеличением номера резонанса. Так, при q =0,05 амплитуды соответствующие первому, второму, третьему резонансам относятся как 1:0,22:0,5. Если в системе присутствуе диссипация, то эта разница будет еще больше. Поэтому при наличии затухания рассматривается обычно главный параметрический резонанс (ω =2 ω 0) как наиболее опасный с минимальным изменением области неустойчивости. При наличии затухания чаще пользуются не диаграммой Айнса-Стретта, а диаграммой относительно частоты возбуждения θ. На рис. 1.6 показаны области относительно частоты возбуждения для главного и второго параметрических резонансов без демпфирования и при декрементах затухания Δ=0,2 и Δ=0,4. Рисунок 1.6 - Области неустойчивости относительно частоты возбуждения θ для главного и второго параметрических резонансов: 1 - область неустойчивости без демпфирования; 2 – область неустойчивости при декременте затухания D = 0,2; 3 – область неустойчивости при декременте затухания D = 0,4
Как следует из рис. 1.6 с увеличением затухания области неустойчивости смещаются выше оси абсцисс и используя демпфирование можно полностью исключить параметрические колебания, если глубина пульсации не достигает областей неустойчивости. Параметрические резонансы подавляются сильнее с увеличением их номера. Для главного параметрического резонанса критическое значение частоты возбуждения равно
где Здесь ω 0 – частота собственных колебаний; для шарнирно-опертого трубопровода Критическое значение частоты возбуждения для второго параметрического резонанса будет иметь следующий вид . Приближенное значение коэффициента возбуждения μ при котором возникает неустойчивость системы будет равно для главного резонанса μ =Δ/ π, для второго резонанса Наряду с введением сопротивления для повышения устойчивости трубопроводов используются динамические гасители колебаний. Установка динамических гасителей позволяет отстроиться от параметрического резонанса. Динамический гаситель колебаний с вязким трением раздваивает главную область параметрического резонанса (см. рис. 1.7). Изменение настройки гасителя по массе и частоте собственных колебаний позволят сдвигать эти области вправо от оси ординат исключая при определенной глубине пульсации попадание в область динамической неустойчивости.
– область неустойчивости без демпфера; – область неустойчивости с демпфером
Постоянно меняющиеся условия эксплуатации в связи с пересеченной местностью, различными частотными и упругими характеристиками грунтов, всплытием трубопроводов и воздействием других факторов делает задачу об устранении параметрического резонанса трубопровода по трассе достаточно сложной. Изменение частотных параметров на разных участках трубопровода (см. рис. 1.8) меняет локальную добротность системы, т.е. ее восприимчивость к внешним воздействиям. При высокой добротности системы, последняя будет реагировать, в первую очередь, на ту часть спектра параметрического возбуждения, частоты которой близки к 2 ω 0. Рисунок 1.8 - Причины, способствующие изменению собственной частоты трубопровода при эксплуатации
Для предупреждения параметрических колебаний трубопровода можно рекомендовать следующие мероприятия: - устранение или уменьшение возбуждающих сил; -стабилизация динамической устойчивости трубопровода путем изменения его параметров; - использование динамических гасителей и демпферов с линейной и нелинейной характеристиками; - демпфирование трубопровода грунтом, подсыпкой. Для уменьшения влияния вибрации от работы поршневых компрессоров необходимо предусмотреть, чтобы фундаменты под компрессоры были отделены от конструкций зданий (фундаментов стен и колонн, перекрытий); площадки между смежными фундаментами компрессоров долны быть вкладными, свободно опирающимися на фундаменты. Трубопроводы, присоединяемые к компрессорам или агрегатам, должны надежно крепиться к конструкциям зданий. Для уменьшения вибрации трубопроводов, вызываемой пульсацией газов, предусматривают буферные емкости. Обвязочные трубопровод ды парообразного холодильного агента должны иметь небольшое число поворотов, а изменение направлений трубопроводов осуществляться с максимальными радиусами. Для изготовления обечаек, трубных пучков, змеевиков, штуцеров, патрубков и других элементов холодильного оборудования, находящихся в рабочем состоянии в контакте с холодильными агентами, следует применять только бесшовные трубы. Но во многих случаях не имеется возможности устранить совсем или уменьшить возбуждающее воздействие, как, например, в случае сейсмического воздействия, то необходимо учитывать стабилизацию динамической устойчивости трубопровода путем изменения его параметров на этапе проектирования. В связи с чем, возникает необходимость в создании математической модели для определения собственной частоты колебаний трубопровода. Краевые и начальные условия В простейших случаях, когда конец стержня свободен, или жестко закреплен, или шарнирно оперт, краевые условия выражаются следующими соотношениями: а) конец стержня свободен; на таком конце равны нулю изгибающий момент и поперечная сила, следовательно,
б) конец стержня жестко закреплен; на таком конце равны нулю прогиб и угол поворота, т. е.
в) в) конец стержня свободно оперт (или закреплен шарниром); в этом случае равны нулю прогиб и изгибающий момент, т. е.
Краевые условия, ограничивающие свободу перемещений концов Стержня, называются геометрическими условиями. Таковы, например, условия, в силу которых равны нулю прогиб и угол поворота, т, е. условия
Условия, налагающие ограничения на изгибающий момент и поперечную силу, например, условия, выражающиеся равенствами
мы будем называть динамическими условиями. В других случаях условия закрепления концов стержня выражаются более сложным образом. Например, при упругом закреплении конца стержня соответствующее такому закреплению краевое условие должно учитывать характер возможных смещений конца и возникающих при этом упругих восстанавливающих сил. Так будет, например, в случае закрепления упругого для поперечных смещений конца и жесткого для поворота или, наоборот, жесткого для поперечных смещений и упругого для поворота и т. д. С такими упругими закреплениями приходится встречаться при расчете на колебания турбинных лопаток, концы которых связаны бандажом, а также при учете упругой податливости заделки хвоста в ободе диска. Отметим, что, оставаясь в пределах линейной теории, мы ограничиваемся рассмотрением краевых условий, выражающихся уравнениями, линейными относительно величин
Начальные условия выражаются соотношениями
имеющими место в момент t=0, где и(х) и v(x)—некоторые заданные функции переменной x, определяющие начальное распределение по оси стержня поперечных отклонений и скоростей отдельных его элементов. ЗАКЛЮЧЕНИЕ В данной магистерской работе были рассмотрены условия, при которых возникают динамические нагрузки в магистральных и технологических трубопроводах. В ходе работы было установлено, что основная задача динамического расчета трубопровода состоит в недопущении в нем резонанса. Для этой цели важной задачей является определение частоты собственных колебаний трубопровода, так как она зависит не от нагрузок, а от конструктивных особенностей трубопровода и является постоянной величиной. Следовательно, зная динамические нагрузки, которые будут действовать на трубопровод в процессе его эксплуатации, на этапе проектирования трубопровода появляется возможность подобрать конструкцию трубопровода с собственной частотой, которая будет обеспечивать его безопасную работу. В ходе работы был проведен ряд исследований с применением моделирования в ANSYS с целью оценки степени влияния расстояния между опорами, типа опор, наличия сосредоточенных масс на частоту собственных колебаний трубопровода, а также коэффициент динамичности. Результаты показали, что частота собственных колебаний и коэффициент динамичности связаны между собой. Чем ниже частоты собственных колебаний, тем выше амплитуды колебаний системы. Частота собственных колебаний резко возрастает, когда в направлении колебаний действуют ограничения на перемещения или же увеличивается жесткость опоры. Важно определить направление возможного колебания трубопровода, чтобы была возможность эти колебания минимизировать. Так, например, изменение расстояния между опорами должным образом влияет только на вертикальные колебания, так как при использовании самых распространенных скользящих опор трубопровод при любом расстоянии не испытывает существенного сопротивления в направлении других осей. Про опоры можно сказать следующее. На колебания, происходящие в вертикальной плоскости их замена мало влияет. Так как изменение их жесткости при замене незначительно по отношению ко всей конструкции в целом и этого недостаточно для существенного изменения частоты колебаний. В то же время, используя опоры, ограничивающие перемещения трубы можно добиться значительного изменения частоты собственных колебаний, действующих в направлении этого ограничения. Отдельно стоит сказать про использование пружинных опор. Они обладают очень высокой податливостью, ввиду, чего при их использовании значительно снижается частота собственных колебаний. Данные результаты лишний раз подтвердили, что они могут значительно обезопасить работу трубопроводов с высокими частотами возмущающих колебаний, например, работающие насосные или компрессорные агрегаты. Наличие сосредоточенных масс оказало положительный эффект на колебания, действующие в горизонтальной плоскости по оси, поперечной трубопроводу. С увеличением массы коэффициент динамичности трубопровода снижался В то же время, в направлении других осей происходит обратная ситуация. В отношении же частот собственных колебаний наличие масс приводит к снижению их значений по всем направлениям, что находит свое применение в динамических гасителях колебаний. Но наличие масс вызывает дополнительные статические нагрузки на трубопровод, а также является металлозатратным ввиду высокой массы. Поэтому данный способ применяют редко, стараясь использовать пружинные опоры.
[1] Упругая ось стержня — это геометрическое место точек («центров жесткости»), к которым должны быть приложены внешние силы, чтобы вызвать изгиб стержня без кручения. Если упругая ось не. совпадает с линией центров тяжести, то, как известно, стержень, Изгибаясь, будет закручиваться. ВВЕДЕНИЕ.. 6 ОБЩИЕ СВЕДЕНИЯ О КОЛЕБАНИЯХ.. 9
|
||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 592; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.196.141 (0.014 с.) |


 (1.1)
(1.1) (1.2)
(1.2) (1.3)
(1.3)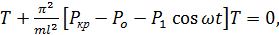 (1.4)
(1.4)
 (1.5)
(1.5) (1.6)
(1.6) (1.7)
(1.7) (1.8)
(1.8)
 ; ε – коэффициент затухания.
; ε – коэффициент затухания. (1.9)
(1.9)