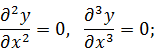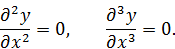Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поперечные колебания прямых стержнейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основные допущения и уравнение поперечных колебаний прямого стержня При выводе уравнения поперечных колебаний стержня (или балки) мы будем предполагать, что в недеформированном состоянии так называемая упругая ось[1] стержня прямолинейна и совпадает с линией центров тяжести поперечных сечений стержня. Эту прямолинейную ось мы примем за координатную ось x: и от нее будем отсчитывать отклонения элементов стержня при поперечных колебаниях. При этом мы будем считать, по крайней мере на первых порах, что отклонения отдельных точек оси стержня происходят перпендикулярно к прямолинейному, недеформированному ее направлению, пренебрегая смещениями этих точек, параллельными оси. Далее, мы предполагаем, что отклонения точек оси стержня при поперечных колебаниях происходят в одной плоскости («плоскость колебаний») и являются «малыми» отклонениями в том смысле, что возникающие при этом восстанавливающие силы остаются в пределах пропорциональности. При таких предположениях отклонения точек оси стержня при поперечных колебаниях однозначно определяются одной функцией двух переменных — координаты x и времени t:
Эта функция удовлетворяет линейному дифференциальному уравнению в частных производных четвертого порядка, которое может быть построено следующим образом. Обозначим через μ(х) массу единицы длины стержня (кГ/м), через EJ—жесткость на прогиб [ Е (Па) — модуль упругости, J(м4) - момент инерции поперечного сечения стержня относительно центральной оси сечения, перпендикулярной к плоскости колебаний], Jв (кГ∙м2) — момент инерции единицы длины стержня относительно центральной оси, перпендикулярной к плоскости колебаний. На стержень действует распределенная поперечная нагрузка, интенсивность которой мы обозначим через f(x,t), а также продольная сила (растягивающая или сжимающая), направленная по оси стержня с интенсивностью Р(x,t). Эти нагрузки могут зависеть не только от положения элементов стержня, но и от времени. Кинетическая, энергия колеблющегося стержня складывается из Кинетической энергии поперечных смещений элементов стержня
и кинетической энергии вращений элементов стержня вокруг осей, перпендикулярных к плоскости колебаний,
Потенциальная энергия равна сумме трех слагаемых: а) потенциальной энергии упругой деформации (работа восстанавливающих упругих сил)
б) потенциальной энергии прогиба от поперечной нагрузки f(x, t)
в) и, наконец, потенциальной энергии растяжения от продольной силы Р(x,t)
Функционал S Остроградского-Гамильтона имеет здесь вид
Уравнение поперечных колебаний стержня мы получим, составив для функционала S уравнение Эйлера
Это линейное уравнение четвертого порядка, составленное при самых общих предположениях относительно действующих на стержень сил, жесткости и распределения массы. В стержнях, длина которых значительно превосходит поперечные размеры, можно пренебречь инерцией вращения и опустить в левой части уравнения (2.7) последний член. Положив f(x,t)=0 и р(х,t)=0, мы рассмотрим сначала свободные колебания однородного стержня с постоянными жесткостью EJ и погонной массой μ. Для таких колебаний уравнение (2.7) будет иметь вид
где Краевые и начальные условия В простейших случаях, когда конец стержня свободен, или жестко закреплен, или шарнирно оперт, краевые условия выражаются следующими соотношениями: а) конец стержня свободен; на таком конце равны нулю изгибающий момент и поперечная сила, следовательно,
б) конец стержня жестко закреплен; на таком конце равны нулю прогиб и угол поворота, т. е.
в) в) конец стержня свободно оперт (или закреплен шарниром); в этом случае равны нулю прогиб и изгибающий момент, т. е.
Краевые условия, ограничивающие свободу перемещений концов Стержня, называются геометрическими условиями. Таковы, например, условия, в силу которых равны нулю прогиб и угол поворота, т, е. условия
Условия, налагающие ограничения на изгибающий момент и поперечную силу, например, условия, выражающиеся равенствами
мы будем называть динамическими условиями. В других случаях условия закрепления концов стержня выражаются более сложным образом. Например, при упругом закреплении конца стержня соответствующее такому закреплению краевое условие должно учитывать характер возможных смещений конца и возникающих при этом упругих восстанавливающих сил. Так будет, например, в случае закрепления упругого для поперечных смещений конца и жесткого для поворота или, наоборот, жесткого для поперечных смещений и упругого для поворота и т. д. С такими упругими закреплениями приходится встречаться при расчете на колебания турбинных лопаток, концы которых связаны бандажом, а также при учете упругой податливости заделки хвоста в ободе диска. Отметим, что, оставаясь в пределах линейной теории, мы ограничиваемся рассмотрением краевых условий, выражающихся уравнениями, линейными относительно величин
Начальные условия выражаются соотношениями
имеющими место в момент t=0, где и(х) и v(x)—некоторые заданные функции переменной x, определяющие начальное распределение по оси стержня поперечных отклонений и скоростей отдельных его элементов.
|
||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1649; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |


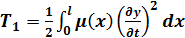 (2.1)
(2.1) (2.2)
(2.2) (2.3)
(2.3) (2.4)
(2.4) (2.5)
(2.5)
 (2.6)
(2.6) (2.7)
(2.7) (2.8)
(2.8)