
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение отрезков заданной длины с помощью поперечного масштабаСодержание книги
Поиск на нашем сайте Условные знаки Условные знаки, которые используются для обозначения на планах и картах различных предметов местности являются едиными для всей России и по характеру изображения подразделяются на 2 группы. · Масштабные (площадные) условные знаки служат для изображения объектов, занимающих значительную площадь и выражающихся в масштабе карты или плана.Площадной условный знак состоит из знака границы объекта и заполняющих его значков или условной окраски.При этом предметы местности изображают с соблюдением масштаба, что дает возможность определить по плану или карте не только местоположение предмета, но и его размеры, форму. · Внемасштабными называются такие условные знаки, которыми предметы местности изображаются без соблюдения масштаба карты или плана, что указывает только на характер и положение объекта в пространстве по его центру (колодцы, геодезические знаки, родники, столбы и т.п.). Эти знаки не позволяют судить о размерах изображаемых местных предметов. Например, на крупномасштабной карте города Томск представлен в виде контура (масштабно); на карте России в виде точки (внемасштабно). По способу изображения на карте условные знаки делят на 3 подгруппы:
Б. Цветовые условные знаки: · отмывка цветом по контуру объекта; · линии и объекты различного цвета. В. Пояснительные условные знаки – дополняют другие условные знаки цифровыми данными, пояснительными надписями (рис. 1.1); ставятся у различных объектов, чтобы охарактеризовать их свойство или качество, например: ширина моста, порода деревьев, средняя высота и толщина деревьев в лесу, ширина проезжей части и общая ширина дороги и т.п. На топографических картах условные знаки указываются в строго определённой последовательности: Пояснения к условным знакам приводятся всегда справа и только на учебных картах. Масштабы Горизонтальные проекции отрезков при составлении карт и планов изображают на бумаге в уменьшенном виде, т.е. в масштабе. Масштаб карты (плана) – отношение длины линии на карте (плане) к длине горизонтальной проекции линии местности:
Масштабы бывают численные и графические. Форма записи численного масштаба: · В виде простой дроби:
где m – степень уменьшения или знаменатель численного масштаба. Например: М 1/2000 (или М = 1:2000). Чем больше значение знаменателя численного масштаба m, тем больше степень уменьшения горизонтальных проекций линий местности и тем мельче масштаб плана или карты. В геодезии наиболее часто применяются следующие масштабы: 1:200, 1:500, 1:1000, 1:2000, 1:5000 - для планов и 1:10000, 1:25000, 1:50000, 1:100000, 1:200000, 1:300000, 1:500000, 1:1000000 – для карт. Указанные соотношения показывают, что горизонтальные проекции линий местности уменьшены на плане соответственно в 500,1000, 2000 и т. д. раз, т. е. отрезку в 1 см на плане соответствуют на местности длины: 500 см (5 м); 1000 см (10 м); 2000 см (20 м) и т. д. · В виде именованного соотношения, например: в 1 см 20 м. При помощи масштабов можно решать следующие задачи. 1. По длине отрезка на плане заданного масштаба определить длину линии на местности. Пусть на карте М Из соотношения следовательно 2. По длине горизонтальной проекции линии определить длину соответствующего отрезка на плане масштаба Пусть горизонтальное проложение между двумя точками на местности равно 400 м. Определить расстояние между этими точками на плане М = 1:2000. Из соотношения
Для того чтобы избежать вычислений и ускорить работу, а также повысить точность измерений на картах и планах, пользуются графическими масштабами: линейным (рис. 1.2) и поперечным (рис. 1.3).
   
Рис. 1.2. Линейный масштаб Линейный масштаб – графическое изображение численного масштаба в виде прямой линии. Для построения линейного масштаба на прямой линии откладывают ряд отрезков одинаковой длины. Исходный отрезок называется основанием масштаба. Крайнее основание делят на части (обычно на 10 частей). Затем линейный масштаб подписывают, исходя из того численного масштаба, для которого он строится (рис. 1.3 для М = 1:10000). Линейный масштаб позволяет оценить отрезок с точностью в 0,1 доли основания точно и до 0,01 доли основания на глаз (для данного масштаба). Для более точных измерений пользуются поперечным масштабом, имеющем на линейном масштабе дополнительное построение по вертикали (рис. 1.3), т.е. поперечный масштаб является разновидностью линейного масштаба. После откладывания необходимого количества оснований масштаба (обычно длиною 2 см, и тогда масштаб называется нормальным) восстанавливают перпендикуляры к исходной линии и делят их на равные отрезки (на m частей). Если основание разделено на n равных частей и точки деления верхнего и нижнего основания соединены наклонными линиями так, как показано на рисунке 1.3, то отрезок

Поперечный масштаб гравируют на металлических линейках, которые называются масштабными. Перед применением масштабной линейки следует оценить основание и его доли по следующей схеме. Пусть численный масштаб 1:5000, именованное соотношение будет: в 1 см 50 м. Если поперечный масштаб нормальный (основание 2 см), то: § одно целое основание масштаба (о.м.) – 100 м; § 0,1 основания масштаба – 10 м; § 0,01 основания масштаба – 1 м; § 0,001 основания масштаба – 0,1 м. Точность масштаба Точность масштаба даёт возможность определить, какие предметы местности можно изобразить на плане, а какие нет из-за их маленьких размеров. Решается и обратный вопрос: в каком масштабе надо составить план, чтобы предметы, имеющие, например, размеры 5 м, были изображены на плане. Для того чтобы в конкретном случае можно было принять определённое решение, вводится понятие точности масштаба. При этом исходят из физиологических возможностей человеческого глаза. Принято, что измерить расстояние, пользуясь циркулем и масштабной линейкой, точнее, чем 0,1 мм, в данном масштабе невозможно (таков диаметр кружка от остро отточенной иглы). Поэтому под предельной точностью масштаба понимают длину отрезка на местности, соответствующую 0,1 мм на плане данного масштаба. Практически принимается, что длина отрезка на плане или карте может быть оценена с точностью ± 0,2 мм. Горизонтальное расстояние на местности, соответствующее в данном масштабе 0,2 мм на плане, называется графической точностью масштаба. Следовательно, в этом масштабе (1:2000) наименьшие различия, которые можно выявить графически, составляют 0,4 м. Точность некоторых других масштабов приведена в табл. 1.1. Точность поперечного масштаба совпадает с точностью графического масштаба.
Таблица 1.1 Сравнительная точность некоторых масштабов
5. Линейные измерения на топографических картах и планах Отрезки, длину которых определяют по карте или плану, могут быть прямолинейными и криволинейными. Однако во всех случаях надо иметь в виду, что для получения необходимой точности измерений угол между плоскостью карты и каждой ножкой измерителя не должен быть меньше 60°, а измерение длины отрезка проводят не менее двух раз. Измерение линейных отрезков Определить линейные размеры объекта на карте или плане возможно с помощью: · линейки и численного масштаба; · циркуля-измерителя и линейного масштаба; · циркуля-измерителя и поперечного масштаба. Измерим отрезок по карте масштаба 1:10000 разными способами и сравним результаты.
Измеряя отрезок линейкой получим, например, 98 мм, или в масштабе – 980 м. Оценивая точность линейных измерений следует учесть, что линейкой можно измерить отрезок длиной не менее 0,5 мм – это величина погрешности линейных измерений при помощи линейки. Измерение отрезков с помощью линейного масштаба проводят в следующем порядке: · взять в раствор циркуля-измерителя отрезок, который необходимо измерить; · приложить раствор циркуля к основанию линейного масштаба, при этом его правую ножку совместить с одним из штрихов основания так, чтобы левая ножка поместилась на основании влево от нуля (на дробном основании); · посчитать количество целых и десятых долей основания масштаба: 1 Измерение расстояний с помощью поперечного масштаба проводят в следующем порядке(рис. 1.4): · оцифровывают поперечный масштаб (нормальный) в масштабе карты (в данном случае 1:10000):
· Берут в раствор циркуля-измерителя отрезок, который необходимо измерить, прикладывают к основанию поперечного масштаба. При этом правую ножку ставят на один из подписанных перпендикуляров так, чтобы и левая ножка оказалась на основании; · поднимают обе ножки измерителя вверх до совпадения левой ножки с каким-либо делением наклонной насечки левого основания масштаба; · подсчитывают число целых оснований по порядковому номеру перпендикуляра; число десятых долей основания – по порядковому номеру наклонной линии; число сотых – по числу делений между основанием и линией, на которой располагаются ножки циркуля; число тысячных (на глаз) – вертикальный отрезок делится на 10 частей и берётся необходимое количество частей.
Рис. 1.4. Измерение отрезка с помощью поперечного масштаба
Запись ведём в следующем виде:
При сравнении результатов измерений одного и того же отрезка с помощью линейки, линейного и поперечного масштабов видно, что более точное число получили при измерении отрезка с помощью поперечного масштаба. Таким образом, работа с поперечным масштабом позволяет более точно (до сотых долей основания масштаба точно и до тысячных долей основания масштаба на глаз) провести линейные измерения. Пример 1. Измерить с помощью поперечного масштаба отрезок в масштабах 1:500 и 1:2000.
1. Оцифровываем масштаб 1:500, измеряем и вычисляем длину отрезка.
2. Оцифровываем масштаб 1:2000, измеряем и вычисляем длину отрезка.
Задание Для выполнения предложенных заданий используют учебную топографическую карту с номенклатурой листа У-35-38-А-в-3. Вариант 1 1. Известна длина линии на карте (2,14 см) и на местности (4280,0 м). Определить численный масштаб карты. 2. Написать именованный масштаб, соответствующий численному 1:500, 1:25000. 3. На плане М 1:5000 отобразить объект, длина которого на местности - 30 м. Определить длину объекта на плане в мм. 4. Определить предельную и графическую точность масштаба 1:1000. 5. При помощи циркуля-измерителя и нормального поперечного масштаба отложить на листе бумаги отрезок 74,4 м в масштабе 1:2000. 6. Определить с помощью поперечного масштаба расстояния между абсолютными отметками точек – 129,2 и 122,1 (квадрат 67-12 учебной карты). 7. Измерить длину ручья (до р. Голубая) (квадрат 64-11) с помощью курвиметра и циркулем-измерителем с раствором 1 мм. Сравнить результаты. Вариант 2 1. Известна длина линии на карте (2,48 см) и на местности (620,0 м). Определить численный масштаб карты. 2. Написать именованный масштаб, соответствующий численному 1:2000, 1:10000. 3. Горизонтальное проложение между двумя точками на плане М 1:1000 составляет 2 см. Определить расстояние между этими точками на местности. 4. Определить предельную и графическую точность масштаба 1:50000. 5. При помощи циркуля-измерителя и нормального поперечного масштаба отложить на листе бумаги отрезок 1415 м в масштабе1:25000. 6. Определить с помощью поперечного масштаба расстояния между абсолютными отметками точек – 141,4 и 146,4 (квадрат 67-12). 7. Измерить длину ручья (до р. Голубая) (квадрат 64-11) с помощью курвиметра и циркулем-измерителем с раствором 1 мм. Сравнить результаты.
ЛАБОРАТОРНАЯ РАБОТА № 2 Тема: Рельеф, его изображение на картах и планах. Чтение рельефа. Решение задач по картам и планам с горизонталями. Построение профиля местности по топографической карте Цель: Ознакомиться с методом изображения рельефа на топографических картах и планах, с элементарными формами рельефа. Освоить определение превышений и абсолютных высот любой точки по карте. Построить профиль местности по линии АВ. Определение отметок точек Рельефомназывают совокупность неровностей поверхности Земли. При строительстве и эксплуатации различных объектов рельеф часто имеет решающее значение, так же как и при решении задач в геологии и геофизике. Для изображения рельефа изобретены различные способы (отмывка, штриховка и т. д.). Однако на современных топографических картах и планах, применяемых для решения инженерных задач, рельеф изображается горизонталями. Чтобы построить рельеф с помощью горизонталей, нужно знать абсолютные отметки точек. Численное значение высоты точкинад основной уровенной поверхностью называется абсолютной отметкой точки H (рис. 2.1 - НA, HB).
При проведении практических съемок часто оказывается целесообразным определять отметки не относительно основной, а относительно условно принятой уровенной поверхности. Такие отметки называются условными (НД, НC). Если известны отметки двух точек, то можно вычислить превышение одной точки над другой (относительную высоту). Так, превышение точки В над точкой А (рис. 2.1) составит:
Основные формы рельефа Рельеф в общем случае разделяют на три вида: равнинный – превышения до 30 м; холмистый – превышения до 200 м; горный – превышения более 200 м. В каждом виде рельефа из всего многообразия можно выделить 6 основных форм. · Гора, холм, сопка (рис. 2.4)– конусообразное возвышение над окружающей местностью. Её наивысшая точка называется вершиной, боковые поверхности – скатами, зона более или менее чёткого перехода горы в окружающий рельеф – подошвой, или основанием, горизонтальные площадки на скате горы – уступами. · · Хребет (рис. 2.6) - возвышенность, вытянутая в одном направлении, скаты которой при пересечении в верхней части образуют водораздел или водораздельную линию. · Лощина (рис. 2.7) - вытянутое углубление местности, постепенно понижающееся в одном направлении. Два ската лощины при пересечении образуют водосливную линию(тальвег). Широкая лощина с пологими скатами называется долиной, узкая лощина с крутыми скатами – оврагом. Скат долины может иметь почти горизонтальные площадки – террасы. Узкое углубление в начале оврага называют промоиной, овраг, заросший травой, называют балкой. Чтобы отличить хребет от лощины необходимо также смотреть бергштрихи и искать оцифрованные горизонтали. · · Крутой обрыв – крутая стенка, вертикальный крутой склон (рис. 2.8).
Характерные линии рельефа: водораздел, водослив.
· Точки, лежащие на одной горизонтали, имеют одинаковую абсолютную высоту. · Горизонтали – непрерывные замкнутые линии (могут выходить за рамку данного плана и замыкаться за его пределами). · Горизонтали относительно параллельны друг другу, никогда не пересекаются (исключение – нависающие или обратные скаты), но могут слиться в одну линию на крутом склоне. · Чем меньше заложение горизонталей d, тем круче скат. Линия, образованная наименьшими d, соответствует направлению наибольшей крутизны. · Всё, что относится к рельефу (горизонтали, цифры, подписи, бергштрихи) изображается коричневым цветом. · Линии водораздела и водослива пересекаются горизонталями под прямым углом. Определение крутизны ската Рассматривая план или карту в горизонталях, мы видим, что взаимные расстояния между горизонталями чрезвычайно разнообразны. Это говорит о различной крутизне поверхности земли. Крутизна ската характеризуется углом наклона линии к горизонту ν (ню) и величиной уклона линии i, которые могут быть как отрицательными, так и положительными. Эти величины определяют по следующим формулам:
где h – высота сечения рельефа, м; d –заложение, м. Уклон линии является отвлечённой величиной и выражается в процентах или промилле (тысячных долях единицы - ‰). Угол наклона выражается в градусах. Пример 5. Рассчитайте уклон линии и угол наклона, если величина заложения в масштабе карты равна 20 м, высота сечения рельефа – 5 м.
Пример6. Между двумя точками з аложение в масштабе карты равно 332 м, а уклон линии составил 0,0028. Найдите превышение
Пример7. Для учебной карты самое маленькое расстояние между горизонталями составляет 1 мм, а самое большое – 5,7 см. Рассчитайте крутизну скатов. Высота сечения рельефа – 2,5 м.
Пример8. Рассчитайте величину заложения, соответствующую уклону 25 промилле, если масштаб плана 1:2000, а высота сечения рельефа 2,5 м.
Пример9. Длина линии, измеренная на местности рулеткой, составила 270 м. Определить длину этой линии на плане масштаба 1:1000, если крутизна ската равна 20˚.
Для избежания расчетов при определении уклонов и наклонов линий по плану или карте на практике пользуются специальными графиками, называемыми масштабами заложений – для углов наклона (рис. 2.11) или для уклонов. Масштабы заложений строятся для определённой высоты сечения рельефа. Для построения графика заложений углов наклона горизонтальную линию делят на равные отрезки произвольной длины и у концов отрезка подписывают значения углов наклона. Затем вычисляют заложения, соответствующие каждому значению угла наклона при принятой высоте сечения рельефа, по формуле
Полученные величины заложений, выраженные в масштабе карты, откладывают на перпендикулярах к горизонтальной линии против соответствующих углов наклона. Полученные точки соединяют (рис. 2.11). Если вместо углов наклона подписать уклоны, то получим график уклонов. Для определения угла наклона или уклона с плана берут в раствор циркуля соответствующее заложение, переносят его на график заложений так, чтобы одна ножка циркуля располагалась на основании, другая – на кривой. Обе ножки измерителя должны быть при этом на одном перпендикуляре к основанию. Пример 10. Построить график заложения углов наклона линии для М 1:5000. Высота сечения рельефа – 5 м (рис. 2.12 [3]).
Задания ВАРИАНТ 1 I. Провести интерполирование горизонталей между точками с абсолютными отметками 212 и 227. Расстояние между точками – 5см. Горизонтали провести через 10 м II. Решить задачи Задача 1. Точка М находится между горизонталями с отметками 125 и 127, 5 м. Найдите абсолютную отметку этой точки, если заложение – 25 мм, расстояние от точки, отметку которой нужно определить, до ближайшей горизонтали (125 м) – 5 мм. Задача 2. На карте приведена замкнутая горизонталь с отметкой 105 м (дно котловины). Найти отметку любой точки (А), расположенной внутри горизонтали, если высота сечения рельефа 5 м. Задача 3. Рассчитайте длину линии на местности, если длина этой же линии на плане масштаба 1:2000 равна 7,08 см, а высотные отметки точек начала и конца линии соответственно равны 98 м и 76 м. Задача 4. Рассчитайте величину заложения, соответствующую уклону 25 промилле, если масштаб плана 1:2000, а высота сечения рельефа 2,5 м. III. Построить профиль местности по линии АВ учебной карты с номенклатурой листа У-35-38-А-в-3.
ВАРИАНТ 2 I. Провести интерполирование горизонталей между точками с абсолютными отметками 57 и 43,3 м. Расстояние между точками – 7 см. Горизонтали провести через 2,5 м II. Решить задачи Задача 1. Точка М находится внутри горизонтали с отметкой 98 м. Отметка характерной точки (дно) – 100 м. Найдите абсолютную отметку точки М, если высота сечения рельефа – 2,5 м; расстояние от характерной точки до горизонтали – 20 мм, расстояние от точки, отметку которой нужно определить, до ближайшей горизонтали по карте – 9 мм. Задача 2. Точка К находится внутри замкнутой горизонтали с отметкой 80 м (дно котловины). Найти отметку точки, расположенной внутри горизонтали, если высота сечения рельефа 5 м. Задача 3. Длина линии на плане масштаба 1:2000 составила 11,05 см. Определить длину этой линии на местности, если её уклон равен 100 промилле. Задача 4. Определить уклон линии АВ, если НВ=47 м, НС=66 м, dВС= 900 м, результат выразить в процентах. III. Построить профиль местности по линии АВ учебной карты с номенклатурой листа У-35-38-А-в-3.
ЛАБОРАТОРНАЯ РАБОТА № 3 Тема: Определение географических и прямоугольных координат по карте или плану Цель: Ознакомиться с географической и прямоугольной системами координат. Освоить определение географических и прямоугольных координат точек по карте Задания Для выполнения предложенных заданий используют учебную топографическую карту с номенклатурой листа У-35-38-А-в-3.
ВАРИАНТ 1 I. Определить географические и прямоугольные координаты точек с абсолютными высотами по учебной карте в квадрате 67-11 2. Найти на карте точки со следующими географическими координатами:
3. Нанести на карту точки со следующими прямоугольными координатами:
4. Определить по учебной карте, какие объекты имеют следующие географические координаты:
5. Определить по учебной карте, какие объекты имеют следующие прямоугольные координаты:
ВАРИАНТ 2 I. Определить географические и прямоугольные координаты точек с абсолютными высотами квадрате 67-12 2. Нанести на карту точки со следующими прямоугольными координатами:
3. Нанести на карту точки со следующими географическими координатами:
6. Определить по учебной карте, какие объекты имеют следующие географические координаты:
7. Определить по учебной карте, какие объекты имеют следующие прямоугольные координаты:
ЛАБОРАТОРНАЯ РАБОТА № 4 Тема: Углы ориентирования в географической системе координат и плоской прямоугольной системе координат Гаусса-Крюгера Цель: Освоить измерение и взаимные пересчёты углов ориентирования в разных системах координат 1. Измерение углов ориентирования на карте или плане в географической системе координат Углы ориентирования в географической системе координат: географический (истинный) азимут прямой, географический (истинный) азимут обратный, географический румб прямой, географический румб обратный. Географический азимут (Аг) – угол, отсчитываемый по часовой стрелке от северного направления географического меридиана до ориентируемой линии. Изменяется от 0˚ до 360˚. Чтобы определить Аг линии АВ необходимо: (рис. 4.1): · провести географический меридиан через начальную точку А; для этого с помощью треугольника провести линию, параллельную географическому меридиану карты; · измерить азимут прямой с помощью транспортира (с точностью до 30´´). Аналогично измеряют азимут географический обратный линии АВ (АгВА), но географический меридиан проводят через точку В. Зная прямой азимут географический линии АВ – АгАВ можно высчитать азимут географический обратный по формулам:
Румбы изменяются от 0˚ до 90˚ и кроме углового значения имеют ещё названия – СВ, ЮВ, ЮЗ, СЗ, например: Обратный румб по значению равен прямому румбу, но имеет противоположное направление. Пример 1. Определить углы ориентирования в географической системе координат линии АВ, заданной на учебной карте (квадрат 68-13, северная часть) (рис. 4.2).
Рис.4.2. Фрагмент учебной топографической карты
Зная азимут географический можно рассчитать румб географический, и наоборот. Пример 2 (рис.4.3). Известен Для решения задачи можно воспользуемся формулами взаимосвязи азимутов и румбов (табл. 4.1). Поскольку линия находится в III четверти, формула пересчёта:
РЕШЕНИЕ
Таблица 4.1 Схема взаимосвязи азимутов и румбов
2. Измерение углов ориентирования на карте и плане в плоской системе координат Гаусса-Крюгера Углы ориентирования в плоской системе координат Гаусса-Крюгера: дирекционный угол прямой, дирекционный угол обратный, румб дирекционный прямой, румб дирекционный обратный, сближение меридианов. Дирекционный угол (a) – угол, отсчитываемый от северного направления осевого меридиана или линии, ему параллельной, по ходу часовой стрелки до ориентируемой линии. Изменяется от 0˚ до 360˚. Дирекционный румб (ra) – угол между ориентируемой линией и ближайшим направлением осевого меридиана или линии, ему параллельной. Изменяется от 0˚ до 90˚. Чтобы найти по карте дирекционный угол линии АВ необходимо (рис. 4.4): · провести осевой меридиан · Обратный дирекционный угол линии АВ – Дирекционному углу плоской системы координат Гаусса-Крюгера соответствует азимут географический, а дирекционному румбу – румб географический; это одни и те же углы, только в разных системах координат. Пример 3. Измерить углы ориентирования в плоской системе координат Гаусса-Крюгера линии АВ, заданной на учебной карте (квадрат 68-13, северная часть).
Измеренные углы ориентирования линии АВ в географической системе координат и плоской системе координат Гаусса-Крюгера отличаются на 2°. Это есть гауссово сближение меридианов (γ) – угол между географическим и осевым меридианами (рис. 4.5).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 11707; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.01 с.) |

 А. Графические условные знаки – линии различной конфигурации (сплошные, пунктирные, штрихпунктирные…), а также комбинации их в виде геометрических фигур. Графические условные знаки используют для изображения объектов линейного типа: дороги, реки, трубопроводы, линии электропередач и т.п., ширина которых меньше точности масштаба данной карты.
А. Графические условные знаки – линии различной конфигурации (сплошные, пунктирные, штрихпунктирные…), а также комбинации их в виде геометрических фигур. Графические условные знаки используют для изображения объектов линейного типа: дороги, реки, трубопроводы, линии электропередач и т.п., ширина которых меньше точности масштаба данной карты.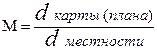 . (1)
. (1) , (2)
, (2) расстояние между точками составляет 5 см. Определить горизонтальное проложение между этими же точками на местности.
расстояние между точками составляет 5 см. Определить горизонтальное проложение между этими же точками на местности. следует:
следует:  ,
,
 .
. найдём
найдём  . Подставив известные значения, получим:
. Подставив известные значения, получим:
 . Соответственно, отрезок
. Соответственно, отрезок 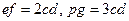 и т.д. Если
и т.д. Если  основания, т.е. такой поперечный масштаб позволяет оценить отрезок точно в 0,01 доли основания, и до 0,001 доли основания – на глаз.
основания, т.е. такой поперечный масштаб позволяет оценить отрезок точно в 0,01 доли основания, и до 0,001 доли основания – на глаз. .
. ;
; ;
; ;
; .
.






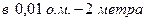








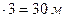







 .
.







 .
.
 (4)
(4)
 Котловина, впадина (рис. 2.5) - замкнутое углубление, самая низкая ее точка – дно, боковые поверхности – скаты, линия перехода в окружающий рельеф – бровка. По характеру изображения на плоскости совпадает с горой. Для отличия этих форм рельефа на карте используют а)бергштрихи, б)проставляют абсолютные отметки в разрывах горизонталей.
Котловина, впадина (рис. 2.5) - замкнутое углубление, самая низкая ее точка – дно, боковые поверхности – скаты, линия перехода в окружающий рельеф – бровка. По характеру изображения на плоскости совпадает с горой. Для отличия этих форм рельефа на карте используют а)бергштрихи, б)проставляют абсолютные отметки в разрывах горизонталей. Седловина (рис. 2.4) – пониженная часть местности между двумя соседними возвышенностями с расходящимися в противоположные стороны лощинами, имеет обычно вид седла. Седловина изображается горизонталями, обращёнными выпуклостями друг к другу.
Седловина (рис. 2.4) – пониженная часть местности между двумя соседними возвышенностями с расходящимися в противоположные стороны лощинами, имеет обычно вид седла. Седловина изображается горизонталями, обращёнными выпуклостями друг к другу. Характерные точки рельефа: вершина горы, дно котловины, самая низкая точка седловины, перегиб ската.
Характерные точки рельефа: вершина горы, дно котловины, самая низкая точка седловины, перегиб ската. 4. Свойства горизонталей
4. Свойства горизонталей ,
,  , (7, 8)
, (7, 8)

 между этими точками.
между этими точками.




 ;
; 


 . (9)
. (9) ,
,





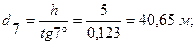

 [4]; (14)
[4]; (14) [5], (15)
[5], (15) где
где  – сближение меридианов в географической системе координат (угол между касательными к меридианам в данных точках, направленных на полярную звезду).
– сближение меридианов в географической системе координат (угол между касательными к меридианам в данных точках, направленных на полярную звезду). ;
; 



 Найти rГ.
Найти rГ. .
.

 через начальную точку ориентируемой линии (А). Для этого приложить треугольник к точке А и провести линию, параллельную осевому меридиану карты;
через начальную точку ориентируемой линии (А). Для этого приложить треугольник к точке А и провести линию, параллельную осевому меридиану карты; измерить дирекционный угол с помощью круглого транспортира (с точностью до 30´´).
измерить дирекционный угол с помощью круглого транспортира (с точностью до 30´´). измеряют таким же образом, только осевой меридиан проводят через точку В.
измеряют таким же образом, только осевой меридиан проводят через точку В.


 Зарамочное оформление учебной карты свидетельствует, что сближение меридианов равно 2°22´,
Зарамочное оформление учебной карты свидетельствует, что сближение меридианов равно 2°22´, 


