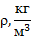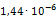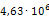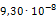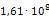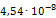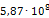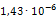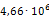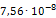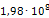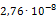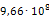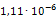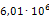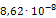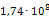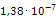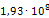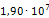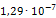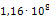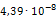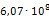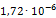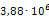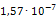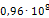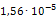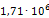Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Влияние типа опоры трубопровода на его динамические характеристикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Существует множество различных видов опор трубопроводов. По характеру работы и назначению опоры можно подразделить на подвижные, к которым относятся скользящие, катковые, шариковые, пружинные и т. п., и неподвижные, которые бывают приварными, хомутовыми и упорными. Подвижные опоры устанавливаются для обеспечения свободного перемещения трубопроводов на опорах при температурных деформациях. Эти опоры воспринимают вертикальную нагрузку — силу тяжести трубопроводов с размещенной на них арматурой и теплоизоляции различных типов, а также горизонтальную нагрузку, зависящую от коэффициента трения на подошве опоры. На величину трения влияет конструкция подвижной опоры. Наиболее распространенными подвижными опорами являются скользящие опоры, перемещающиеся вместе с трубой по различным опорным конструкциям; коэффициент трения для скользящей опоры принимают равным 0,3. Для организации более свободного перемещения трубопровода применяют катковые опоры с коэффициентом трения 0,1, Шариковые опоры воспринимают горизонтальные осевые и боковые нагрузки. Пружинные опоры применяются для поглощения вибрации, передаваемой от технологического оборудования, и обеспечивают надежную работу как сварных, так и фланцевых соединений. Неподвижные (мертвые) опоры устанавливают на трубопроводах для обеспечения поглощения линейных удлинений при температурных перепадах транспортируемой среды. Кроме вертикальных нагрузок от собственного веса трубопровода, изоляции и др. неподвижные опоры воспринимают весьма значительные горизонтальные усилия, возникающие при температурных деформациях. Между неподвижными опорами, как правило, устанавливаются компенсаторы. Горизонтальные усилия, действующие на неподвижные опоры, можно подразделить на осевые и боковые: осевые — передаются на все неподвижные опоры, боковые — на опоры, расположенные вблизи поворотов трубопровода и в местах подсоединения их вблизи опор. Горизонтальные усилия и расстояния между неподвижными опорами определяются соответствующими расчетами. Различные типы опорных конструкций показаны на рис. 3.5.
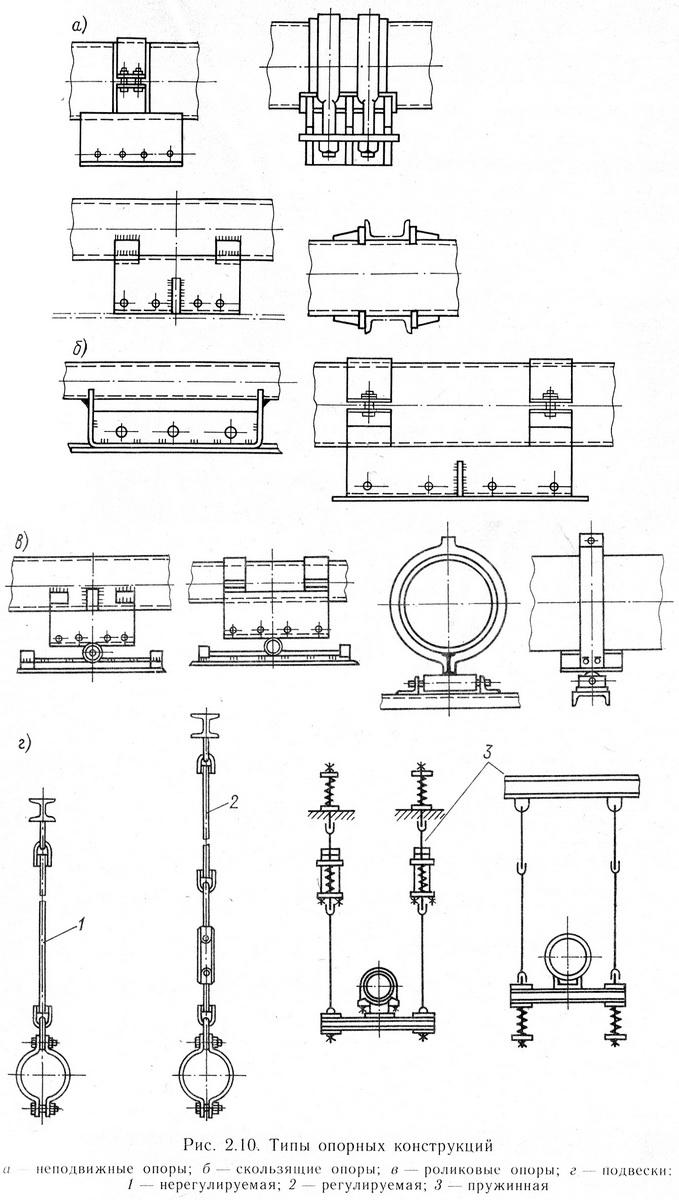
Рисунок 3.5 - Типы опорных конструкций. А – неподвижные опоры; б – скользящие опоры; в – роликовые опоры; г – подвески:
1 – нерегулируемая; 2 – регулируемая; 3 – пружинная. Рассмотрим как влияет выбор типа опоры на коэффициент динамичности трубопровода. Для расчета было выбрано 5 типов опор по ОСТ 36-146-88: - КП-АС21 - опора корпусная приварная высотой 150мм и длиной 170мм; - КП-АС22 - опора корпусная приварная высотой 150мм и длиной 340мм; - КП-АС11 - опора корпусная приварная высотой 100мм и длиной 170мм; - КХ-АС21 - опора хомутовая высотой 150мм и длиной 170мм; - КН-АС11 - опора хомутовая высотой 170мм и длиной 200мм. Модели данных опор представлены на рис. 3.6.
Рисунок 3.6 – Модели опор. Для того чтобы упростить модель и снизить время расчета, выполним моделирование в несколько этапов. Для начала определим жесткости опор в направлении осей координат. Для каждой из опор решается серия задач о нахождении деформированного состояния опоры под действием различных усилий, приложенных к трубе, которая моделируется как “абсолютно твердое тело” (модуль Юнга на несколько порядков превышает модуль Юнга стали). Задачи решаются с учетом контактного взаимодействия опоры и участка трубы. При вычислении каждой трансляционной жесткости к трубе прикладывается сила F, направленная вдоль одной из осей (рис. 3.7). Рисунок 3.7 – Схема приложения нагрузок для определения жесткости опоры. В результате КЭ решения данных задач по полученным деформированным состояниям опоры определяются соответствующие жесткости. Трансляционная жесткость опоры Ki в i-ом направлении вычисляются следующим образом. Деформация упругого элемента под действием приложенной силы определяется по следующей формуле (рис.3.8):
где Р – приложенная сила, l – длина элемента, E – модуль Юнга, равный для стали F – площадь поперечного сечения элемента.
Рисунок 3.8 – Расчетная схема определения жесткости опор.
Жесткость является обратной величиной деформации. Если принять силу равной 1Н, то получим искомую жесткость элемента.
Для упрощения расчета определим реальные трансляционные жесткости опор и затем при расчете трубопровода заменим опоры на кубические элементы с размерами 200х100х150мм (ДхШхВ), обладающие жесткостью, эквивалентной реальным опорам (рис. 3.9).
Рисунок 3.9 – Эквивалентная опора.
Эквивалентной жесткости можно добиться путем изменения любых параметров формулы (3.4) таким образом, чтобы жесткость К оставалась неизменной. Мы же добьемся эквивалентной жесткости путем изменения модуля Юнга. Для каждого из направления действия вычмслим его значение по формуле:
Приведем пример расчета одной из опор на примере опоры 219-КП-АС21. В направлении оси Х к торцам трубопровода приложены силы, равные 1Н. В связи с тем, что силы две, то P=2Н. Значение l здесь будет принимать ширина опоры, равная 100мм. После расчета деформаций определили максимальную деформацию опоры в направлении оси Х, равное
Аналогичным образом определим все остальные значения модуля Юнга. Результаты расчета сведены в таблицу 3.2. Кроме жесткости опор также следует пересчитать плотности материала эквивалентных опор, чтобы их массы соответствовали значениям реальных опор. Так, например, реальная масса m опоры 219-КП-АС21 составляет 3,4кг. Модель эквивалентной опоры имеет объем V равный 0,003 м3. Таким образом, эквивалентная плотность материала данной опоры составит:
Значения плотностей для остальных опор также сведены в таблицу 3.2. Таблица-3.2. Результаты определения жесткостей опор.
При моделировании опор в ANSYS для них задается новый материал, обладающий ортотропными свойствами. Для каждого направления осей координат задаются определенные выше значения модуля Юнга, а также плотность материала. Модальный и гармонический анализ определены для того же трубопровода, что и в пункте 3.2. Расстояние между опорами трубопровода принято равным 9м. Граничные условия для всех трубопроводов аналогичны, за исключением опоры 219-КН-АС11. Так как данная опора является направляющей, то на нее наложено дополнительное ограничение по перемещениям в горизонтальном направлении поперечном оси трубопровода. Результаты расчетов приведены в таблице 3.3 и на рис. 3.10. Таблица-3.3. Результаты анализа частот собственных колебаний при изменении типа опоры.
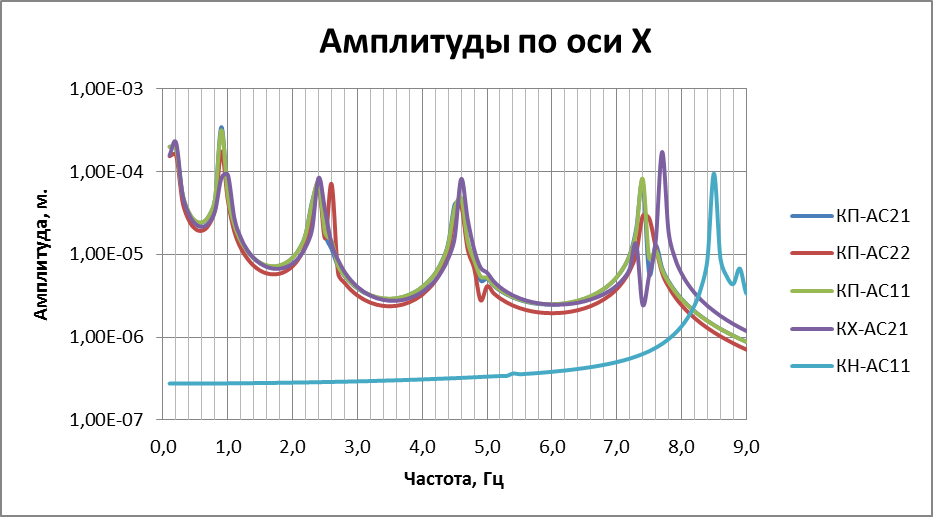
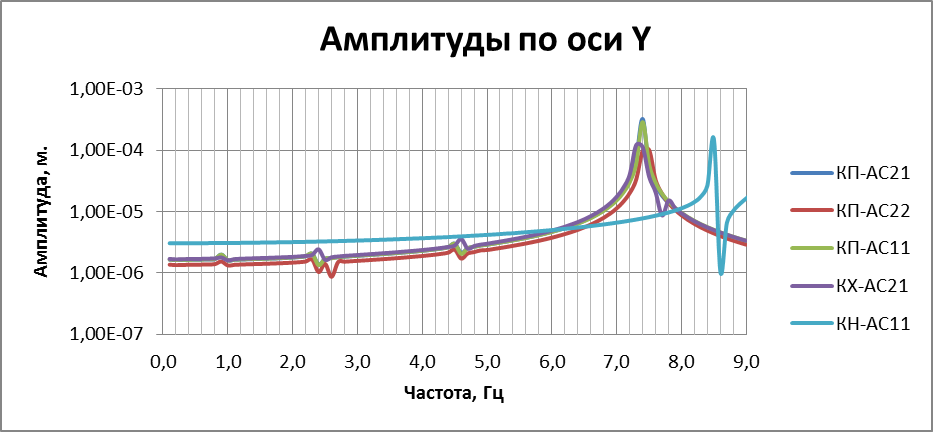
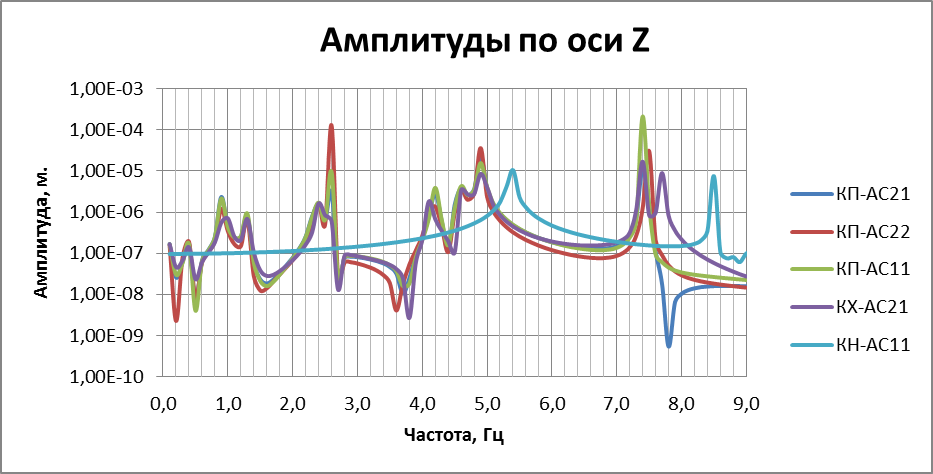
Рисунок 3.10. Спектры отклика в зависимости от типа опоры. Как видно из результатов анализа, собственные частоты ненаправляющих опор различаются между собой в пределах до 5%. Спектры отклика системы на гармоническое возмущение для них также лежат в близких друг к другу границах. Сильно отличаются среди всех результаты расчета для катковой направляющей опоры. Частоты ее собственных колебаний значительно выше, чем у других опор, а коэффициент динамичности – ниже. На основании этого можно сделать вывод, что жесткость опоры мало влияет на динамические свойства системы. Это происходит ввиду того, что на динамику конструкции влияют прежде всего ее масса и геометрические параметры. Если же между собой опоры и имеют значительные различия в жесткости и массе, то в масштабах всей конструкции эта разница малозаметна.
В свою очередь, граничные условия опирания оказывают значительное влияние на динамику системы. Это хорошо наблюдалось на примере направляющей опоры. Наложение дополнительного ограничения на перемещения увеличило частоту собственных колебаний, снизив при этом значения перемещений.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 765; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.239.63 (0.009 с.) |

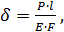 (3.3)
(3.3)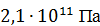 ,
,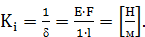 (3.4)
(3.4)
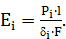 (3.4)
(3.4)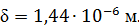
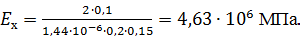 (3.5)
(3.5) (3.6)
(3.6)