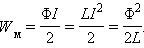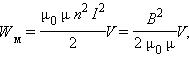Эдс, возникающая в проводниках, движущихся в магнитном поле

ЭДС индукции возникает либо в неподвижном замкнутом проводнике, помещённом в изменяющееся во времени магнитное поле, либо в проводнике, движущемся в магнитном поле, которое может и не меняться со временем. ЭДС индукции в обоих случаях рассчитывается по формуле

Сила Лоренца вызывает перемещение электронов в проводниках, движущихся в магнитном поле.

 

6. Вихревые поля

Причина возникновения электрического тока в неподвижном проводнике - электрическое поле.

Всякое изменение магнитного поля порождает индукционное электрическое поле независимо от наличия или отсутствия замкнутого контура, при этом если проводник разомкнут, то на его концах возникает разность потенциалов; если проводник замкнут, то в нем наблюдается индукционный ток.

Индукционное электрическое поле является вихревым.

Направление силовых линий вихревого эл. поля совпадает с направлением индукционного тока

Индукционное электрическое поле имеет совершенно другие свойства в отличии от электростатического поля.

Вихревое электрическое поле возникает в случае изменения ектора магнитной индукции внешнего поля.

 

Связь электрического и магнитного полей

Магнитное поле способно в определенных условиях порождать электрическое без помощи зарядов, а электрическое — непосредственно порождать магнитное. Именно так: магнитное поле рождает только электрическое, а электрическое — только магнитное, которое, правда, в свою очередь может породить электрическое.

 

Самоиндукция

Самоиндукция - явление возникновения ЭДС индукции в эл.цепи в результате изменения силы тока.

Возникающая при этом ЭДС называется ЭДС самоиндукции

Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре. Данное явление называется самоиндукцией, а соответствующее значение - ЭДС самоиндукции.

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней

 

Индуктивность

Индуктивностью (от латинского inductio - наведение, побуждение), называется величина, характеризующая связь между изменением тока в электрической цепи и возникающей при этом ЭДС (электродвижущей силы) самоиндукции. Индуктивность обозначается большой латинской буквой «L», в честь немецкого физика Ленца. Термин индуктивности предложил в 1886 году Оливер Хевисайд.,

 

Величина магнитного потока, проходящего через контур, связана с силой тока следующим образом: Φ = LI. Коэффициент пропорциональности L называется коэффициентом самоиндукции контура или просто индуктивностью. Значение индуктивности зависит от размеров и формы контура, а также от магнитной проницаемости среды. Единицей измерения индуктивности является Генри (Гн). Дополнительные величины: мГн, мкГн.

 

Зная индуктивность, изменение силы тока и время этого изменения, можно найти ЭДС самоиндукции, которая возникает в контуре:

Через индуктивность выражают также энергию магнитного поля тока:

Соответственно чем больше индукция, тем больше магнитная энергия, накапливаемая в пространстве вокруг контура с током. Индуктивность является своеобразным аналогом кинетической энергии в электричестве.

 

7. Индуктивность соленоида.

L - Индуктивность (соленоида), размерность в CИ Гн

L - Длина (соленоида), размерность в СИ - м

N - Число (витков соленоида

V- Объём (соленоида), размерность в СИ - м3

- Относительная магнитная проницаемость

- Магнитная постоянная Гн/м

 

Энергия магнитного поля соленоида

Энергия Wм магнитного поля катушки с индуктивностью L, создаваемого током I, равна

Применим полученное выражение для энергии катушки к длинному соленоиду с магнитным сердечником. Используя приведенные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, можно получить: