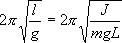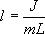Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параметры колебательного движенияСодержание книги Поиск на нашем сайте
1. Смещение х - отклонение колеблющейся точки от положения равновесия в данный момент времени (м). 2.Амплитуда хм - наибольшее смещение от положения равновесия (м). Если колебания незатухающие, то амплитуда постоянна. 3. Период Т — время, за которое совершается одно полное колебание. Выражается в секундах (с).
4. Частота n — число полных колебаний за единицу времени. В СИ измеряется в герцах (Гц). Частота колебаний равна одному герцу, если за 1 секунду совершается 1 полное колебание. 1 Гц= 1 с-1.
5. Циклической (круговой) частотой w периодических колебаний наз. число полных колебаний, которые совершаются за 2p единиц времени (секунд). Единица измерения – с-1.
6. Фаза колебания - j - физическая величина, определяющая смещение x в данный момент времени. Измеряется в радианах (рад). Фаза колебания в начальный момент времени (t=0) называется начальной фазой (j0).
Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом: x(t) = Asin(ωt + φ)
или x(t) = Acos(ωt + φ),
Графики функций f(x) = sin(x) и g(x) = cos(x) на декартовой плоскости.
где х — значение изменяющейся величины, t — время, остальные параметры - постоянные: А — амплитуда колебаний, ω — циклическая частота колебаний, (ωt + φ) — полная фаза колебаний,
Обобщенное гармоническое колебание в дифференциальном виде
2. Колебание груза на пружине Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению F (t) = ma (t) = –m ω2 x (t)
Частота ω0 называется собственной частотой колебательной системы. Период T гармонических колебаний груза на пружине равен
3. Математическим маятником называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. Колебания маятника при больших амплитудах не являются гармоническими. Для малых колебаний математического маятника второй закон Ньютона записывается в виде
Формула Гюйгенса
4. Физический маятник
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения
Решение этого уравнения
Определим длину l математического маятника, при которой период его колебаний равен периоду колебаний физического маятника, т.е.
Из этого соотношения определяем
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 949; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.101.51 (0.006 с.) |

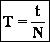
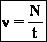
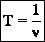
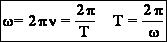
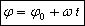
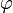 — начальная фаза колебаний.
— начальная фаза колебаний.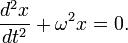
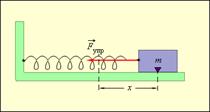 Круговая частота ω0 свободных колебаний груза на пружине находится из второго закона Ньютона:
Круговая частота ω0 свободных колебаний груза на пружине находится из второго закона Ньютона: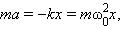 откуда
откуда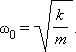
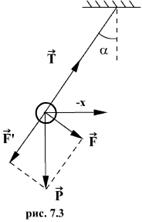
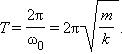
 Математический маятник.
Математический маятник.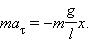
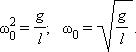
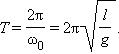
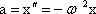
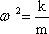
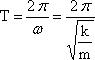
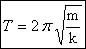
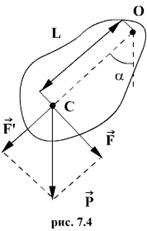 Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной.
Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной.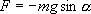
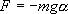
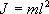 Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид:
Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид: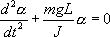
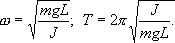
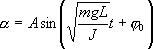
 или
или