
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Действие магнитного поля на заряды и токиСодержание книги
Поиск на нашем сайте
Сила Лоренца На частицу с зарядом q, движущуюся со скоростью
Эта сила называется силой Лоренца. Модуль силы Лоренца равен:
где Так как
Полное ускорение частицы равно нормальному ускорению
где m – масса движущейся частицы. На характер движения частицы значительно влияет угол Рассмотрим частный случай однородного магнитного поля. 1. Если заряженная частица влетает в однородное магнитное поле параллельно линиям магнитной индукции, т. е. 2. Если заряженная частица влетает в однородное магнитное поле перпендикулярно линиям индукции (поперечное магнитное поле) (рис. 26), т. е.
откуда следует, что
Из (2.1) и (2.2) следует, что сила Лоренца
и лежит в плоскости, перпендикулярной к вектору магнитной индукции Таким образом, движение частицы можно представить как суперпозицию двух движений: перемещение вдоль направления
Время T, которое частица затрачивает на один оборот, найдем, разделив длину окружности
Результирующее движение происходит по винтовой траектории, ось которой совпадает с направлением
Направление закручивания винтовой траектории зависит от знака заряда частицы (рис. 26 и 27). Эффект Холла Пусть по проводнику прямоугольного поперечного сечения (b – ширина, а – толщина образца) течет постоянный электрический ток, I – сила тока. Если образец поместить в однородное магнитное поле, перпендикулярное двум его граням (на рис. 28 это передняя и задняя грани), то между двумя другими гранями возникает разность потенциалов. Это явление было обнаружено Холлом и называется эффектом Холла. Разность потенциалов между гранями называется эдс Холла Эффект Холла объясняется следующим образом. В отсутствие магнитного поля в проводнике существует лишь продольное электрическое поле

 , направленная перпендикулярно вектору магнитной индукции и току, модуль которой , направленная перпендикулярно вектору магнитной индукции и току, модуль которой 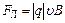 . .
В результате действия этой силы носители тока смещаются в поперечном направлении. На одной грани пластинки образуется избыток отрицательных зарядов, а на другой соответственно избыток положительных. Таким образом, появляется дополнительное поперечное электрическое поле, напряженность
Отсюда
где Сила тока I связана со скоростью упорядоченного движения электронов соотношением [5]:
где S – площадь прямоугольного поперечного сечения образца шириной b и толщиной а; j – плотность тока; n – концентрация носителей тока. Таким образом, из (2.9) и (2.10) получаем значение эдс Холла
|
||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.255.103 (0.007 с.) |

 в магнитном поле, индукция которого равна
в магнитном поле, индукция которого равна 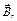 действует сила
действует сила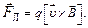 (2.1)
(2.1) (2.2)
(2.2)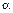 – угол между векторами
– угол между векторами 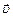 и
и 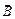 . Направление силы Лоренца зависит от знака заряда и всегда перпендикулярно плоскости, содержащей вектора
. Направление силы Лоренца зависит от знака заряда и всегда перпендикулярно плоскости, содержащей вектора 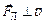 , работа силы Лоренца, равная скалярному произведению силы на элементарное перемещение, равна нулю [6]. Следовательно, кинетическая энергия и скорость частицы при ее движении в магнитном поле остаются постоянными по своей величине. Таким образом, сила Лоренца изменяет вектор скорости только по направлению, поэтому тангенциальное ускорение частицы [6]
, работа силы Лоренца, равная скалярному произведению силы на элементарное перемещение, равна нулю [6]. Следовательно, кинетическая энергия и скорость частицы при ее движении в магнитном поле остаются постоянными по своей величине. Таким образом, сила Лоренца изменяет вектор скорости только по направлению, поэтому тангенциальное ускорение частицы [6] .
.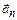 , тогда по второму закону Ньютона
, тогда по второму закону Ньютона , (2.3)
, (2.3)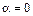 , то
, то 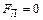 . В этом случае частица не отклоняется от направления своего движения, двигаясь вдоль линий индукции магнитного поля.
. В этом случае частица не отклоняется от направления своего движения, двигаясь вдоль линий индукции магнитного поля.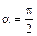 , то из (2.2) и (2.3) следует, что
, то из (2.2) и (2.3) следует, что 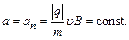
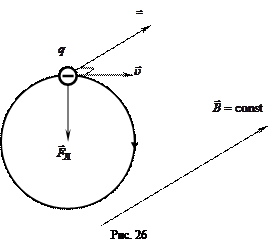 Таким образом, в однородном поперечном магнитном поле заряженная частица будет двигаться равномерно по окружности в плоскости, перпендикулярной вектору магнитной индукции (рис. 26). Радиус окружности R определяется из соотношения для центростремительного ускорения:
Таким образом, в однородном поперечном магнитном поле заряженная частица будет двигаться равномерно по окружности в плоскости, перпендикулярной вектору магнитной индукции (рис. 26). Радиус окружности R определяется из соотношения для центростремительного ускорения: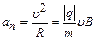 ,
,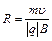 . (2.4)
. (2.4) 3. Выясним характер движения заряженной частицы в случае, когда угол
3. Выясним характер движения заряженной частицы в случае, когда угол  . Разложим вектор
. Разложим вектор 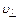 – перпендикулярную
– перпендикулярную 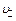 – параллельную
– параллельную  ,
,  .
.
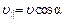 и равномерное движение по окружности со скоростью
и равномерное движение по окружности со скоростью  на
на 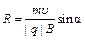 . (2.5)
. (2.5)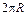 на скорость частицы
на скорость частицы  . (2.6)
. (2.6) на время одного оборота:
на время одного оборота: . (2.7)
. (2.7)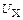 .
.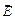 , обусловливающее ток. Эквипотенциальные поверхности этого поля перпендикулярны вектору
, обусловливающее ток. Эквипотенциальные поверхности этого поля перпендикулярны вектору 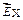 которого в итоге достигает такого значения, что электрическая сила, равная
которого в итоге достигает такого значения, что электрическая сила, равная 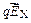 , уравновешивает силу Лоренца
, уравновешивает силу Лоренца 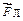 . В результате устанавливается равновесие, при котором
. В результате устанавливается равновесие, при котором . (2.8)
. (2.8)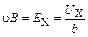 , (2.9)
, (2.9) (2.10)
(2.10)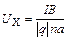 . (2.11)
. (2.11) В заключение заметим, что эффект Холла дает достаточно простой способ экспериментального определения концентрации носителей тока, а в случае полупроводников – типа их проводимости (по знаку эдс Холла). Если же концентрация носителей заряда известна, эффект Холла может быть использован для измерения магнитной индукции (датчики Холла).
В заключение заметим, что эффект Холла дает достаточно простой способ экспериментального определения концентрации носителей тока, а в случае полупроводников – типа их проводимости (по знаку эдс Холла). Если же концентрация носителей заряда известна, эффект Холла может быть использован для измерения магнитной индукции (датчики Холла).


