
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды машин переменного тока и их устройствоСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте ЭДС обмоток переменного тока
При проектировании МПрТ стремятся к такому, чтобы их ЭДС имела синусоидальную форму. В машинах, в которых ЭДС наводится в обмотках, вращающимся полем индуктора, форма кривой ЭДС зависит от распределения индукции в воздушном зазоре. Чтобы обеспечить синусоидальную форму ЭДС, надо приблизить распределение индукции в воздушном зазоре к синусоидальному.
ЭДС проводника, витка и катушки
Вопросы наведения ЭДС в обмотке переменного тока удобно рассматривать на примере СМ. С этой целью удобно часть машины, соответствующую двойному полюсному делению изобразить в развернутом виде (рис.1.6). При вращении индуктора первая гармоника индуктирует в каждом из проводников ЭДС
где
Здесь
где На рис. 1.6 указаны следующие обозначения:
Следовательно, максимальное и действующее значения ЭДС проводника будут:
Нередко в машинах выполняют пазы со скосом по длине. В этом случае начало и конец проводника оказываются сдвинутыми относительно друг друга на угол γ
где Можно разбить проводник на малые участки по длине. В разное время эти участки будут находится под различным воздействием поля. Следовательно, ЭДС этих участков будут сдвинуты во времени относительно друг друга. Так, например, ЭДС начального и конечного участка будут сдвинуты на угол ЭДС всего проводника в данном случае будет равна геометрической сумме ЭДС отдельных участков, причем сумма геометрическая меньше суммы арифметической. Уменьшение ЭДС проводника при наличии скоса пазов характеризуется коэффициентом скоса. Если участки принять бесконечно малыми, то геометрическая сумма их ЭДС изобразится дугой, а ее величина – хордой дуги, опирающейся на угол
Определим ЭДС витка. Виток – совокупность двух последовательно соединенных проводников, расположенных на расстоянии равном или близком к полюсному делению. Шаг витка обозначается у (рис. 1.9). При диаметральном или полном шаге витка (
ЭДС проводников можно изобразить в виде противоположно направленных векторов. Величина ЭДС витка в данном случае
В машинах переменного тока часто прибегают к укорочению шага (см. рис. 1.9). В этом случае ЭДС проводников, составляющих виток, будут сдвинуты не на π, а на угол Величина ЭДС витка с укороченным шагом (
Здесь Окончательно
Обмотки, как правило, выполняются из катушек. Катушка – совокупность нескольких последовательно соединенных витков
ЭДС катушечной группы
Обмотки машин переменного тока, как правило, выполняются из катушечных групп. Катушечная группа – это совокупность q последовательно соединенных катушек, катушечные стороны которых расположены в q соседних пазах.
Угол, который соответствует катушечной группе в пределах одного или двух полюсных делений, называют углом фазной зоны. В машинах переменного тока применяют симметричные трехфазные обмотки шестизонные и трехзонные. В первом случае угол фазной зоны 60˚, во втором случае угол фазной зоны 120˚. В случае шестизонной обмотки в пределах каждого полюсного деления размещаются три фазы, при этом на каждую фазу приходится одинаковое число пазов
При вращении первая гармоника поля наводит в катушках ЭДС, сдвинутые во времени по фазе на угол
Для определения ЭДС катушечной группы следует геометрически сложить ЭДС отдельных катушек. При этом сумма геометрическая меньше суммы арифметической ЭДС катушек. Отношение величины геометрической суммы к сумме арифметической – коэффициент распределения. Он характеризует уменьшение ЭДС катушечной группы из
В результате ЭДС катушечной группы с учетом скоса, укорочения и распределения
Здесь Фазная обмотка обычно состоит из нескольких катушечных групп, соединенных последовательно, последовательно–параллельно или параллельно. ЭДС фазы равна ЭДС параллельной ветви. Если в этой параллельной ветви имеется n последовательно соединенных катушечных групп, то
Здесь
Классификация обмоток
В машинах переменного тока применяются следующие виды обмоток. 1. Обмотки, расположенные в пазах статора или ротора, и подключенные к внешней цепи. 2. Обмотки, расположенные в пазах статора или ротора и замкнутые накоротко. 3. Обмотки, по которым протекает постоянный ток, например, обмотки возбуждения синхронной машины, создающие магнитное поле. Простейшим элементом обмотки является виток, представляющий совокупность двух последовательно соединенных проводников находящихся на расстоянии близком или равном Катушечные обмотки изготавливаются в виде катушек вне машины, а затем укладываются в пазы. Стержневые обмотки выполняются из стержней – полукатушек. Они также могут укладываться через отверстия в пазы. Если пазы полузакрытые, то стержни укладываются в них с торцов.
Пазы могут быть: · открытыми (рис.1.15,а); · полуоткрытыми (рис.1.15,б); · полузакрытыми (рис.1.15,в,г); · закрытыми (рис.1.15,д).
По форме: · прямоугольными (рис.1.15,а,б); · трапециевидными (рис.1.15,в); · овальными (рис.1.15,г); · круглыми (рис.1.15,д). Обмотки АМ могут быть однослойными и двухслойными. Однослойные обмотки
При изучении обмоток переменного тока, как и при изучении обмоток якоря машины постоянного тока, удобно пользоваться развёрнутыми схемами. Под схемой-развёрткой понимают цилиндрическую поверхность статора или ротора, видимую со стороны пазов, разрезанную по одной из образующих цилиндра и развёрнутую в плоскость. При построении развертки обмотки, задаются следующие данные: z – число пазов; Рассмотрим принцип образования схемы трёхфазной однослойной обмотки при следующих данных:
На каждом полюсном делении размещены пазы, принадлежащие трём фазам, причем каждой фазе принадлежит одинаковое число пазов q=2. Все 24 паза делятся равномерно на 3 фазы. На каждую фазу приходится по 8 пазов: фазе В пределах каждой фазы катушечные стороны расположены в восьми пазах и могут соединяться по-разному (рис. 1.17). В связи с этим возможно несколько вариантов обмотки. Рассмотрим некоторые из них.
Двухслойные обмотки
Обмотка укладывается в пазах в два слоя. В верхнем слое одного паза укладывается одна сторона катушки, а другая сторона – в нижем слое другого паза, сдвинутого на шаг. Двухслойная обмотка позволяет получить любое желаемое укорочение шага, и следовательно, обеспечить нужную форму кривой ЭДС. Укорочение шага позволяет резко понизить расход меди на лобовые соединения. Двухслойные обмотки выполняются как петлевыми, так и волновыми. Петлевые выполняют из многовитковых катушек (секций). Эти катушки изготовляются вне машины, хорошо изолируются и в готовом виде укладываются в открытые пазы. Если пазы полузакрытые, то обмотка выполняется из мягких секций, которые изготовляются вне машины из круглого провода, а затем по одному проводку упаковываются (всыпаются в паз). Такие обмотки называются всыпными. Двухслойные обмотки могут иметь целое число пазов на полюс и фазу Двухслойные обмотки отличаются от обмотки якоря машины постоянного тока. Рассмотрим образование двухслойной шестизонной трёхфазной обмотки из обмотки якоря машины постоянного тока при 2р=2. Обмотку якоря такой машины можно разделить на 6 частей – катушечных групп (рис. 1.20). В рассматриваемом случае каждая из фаз образуется последовательным соединением катушечных групп сдвинутых в общем случае на 1800 эл. градусов, причём ЭДС этих групп складываются. Катушечные группы в пределах каждой фазы можно также соединить параллельно, тогда каждая фазная обмотка будет состоять из двух параллельных ветвей.
Рассмотрим принцип образования трёхфазной, двухслойной петлевой обмотки с полным шагом при следующих данных:
Как следует из схемы (рис. 1.21), фаза U состоит из четырёх последовательно соединённых катушечных групп. Фазы V и W выполняются аналогично со сдвигом на 1200 эл. град, то есть на В общем случае число последовательно соединённых катушечных групп в фазной обмотке равно Пример двухслойной петлевой обмотки с укороченным шагом (рис. 1.22). Рассмотрим принцип образования такой обмотки:
Порядок соединения катушечных сторон влияет на величину ЭДС обмотки, следовательно, в данном случае двухслойную обмотку с укороченным шагом можно представить как совокупность двух однослойных обмоток расположенных в верхнем и нижнем слоях и сдвинутых друг от друга на угол укорочения шага. Однослойные обмотки при этом имеют полный шаг. Заметим, что в данном случае лишь в части пазов лежат катушечные стороны, принадлежащие одной фазе. В других пазах расположены катушечные стороны разных фаз. Рассматриваемая петлевая обмотка имеет межгрупповые и межкатушечные соединения, что увеличивает расход меди. Кроме того, наличие витковой изоляции, в случае многовитковой секции, ухудшает использование паза. Поэтому в ряде случаев предпочтение отдается стержневой обмотке волнового типа. В этом случае в пазу укладывается лишь два массивных стержня: один в верхнем, другой в нижнем слое паза. Эти обмотки применяются в мощных машинах (ГГ и ТГ), имеющих мощный поток и большее число катушек. Катушки выполняются с числом витков Рассмотрим принцип образования стержневой обмотки волнового типа при следующих данных (рис. 1.23): В данном случае при выполнении схемы обмотки делаются волны. После первого обхода волна сдвигается влево на 1 паз и, следовательно, обмотка с укороченным переходом. У нас сделано 2 цикла обходов, один влево, другой вправо. Каждый цикл состоит из двух обходов и содержит 2рq последовательно соединённых катушечных групп. В рассмотренном случае обмотку можно выполнить с числом параллельных ветвей а=2 по числу циклов обхода.
МДС катушки
При изучении МДС обмоток переменного тока делаются следующие допущения: а) магнитная проницаемость стальных участков магнитопровода б) выступающие полюса и паза отсутствуют и зазор равномерен; в) катушечные стороны обмотки расположены непосредственно в воздушном зазоре и в сечении имеют вид тонких лент с шириной δ; г) воздушный зазор очень мал по сравнению с радиусом расточки статора и величиной полюсного деления. Указанные допущения наиболее близки в действительности в АМ, у которых, расточка статора и ротор имеют цилиндрическую форму. Пусть на статоре АМ размещена простейшая обмотка с полным шагом
Катушечный ток При протекании тока, катушка создаёт пульсирующее магнитное поле. МДС действующая по каждому из контуров 1,2 и т.д. может быть определена по закону полного тока:
Так как согласно первому допущению
или
Здесь
причем Отметим, что МДС катушки пульсирует во времени по закону синуса, причем
где
Так как
где Тогда где Таким образом, МДС катушки в любой момент времени и в любой точке пространства, удалённой на расстояние x от оси катушки, может быть представлена как сумма основной и высших пространственных гармоник, пульсирующих во времени по закону синуса с одинаковой частотой.
МДС катушечной группы
Как известно, катушечная группа представляет собой совокупность последовательно соединённых q катушек, катушечные стороны которых в пределах полюсного деления размещены в соседних пазах. При
Указанные гармоники МДС катушек можно представить в виде пространственных векторов, сдвинутых на угол α (рис. 1.25,б). Максимальная амплитуда первой гармоники МДС катушечной группы может быть получена геометрическим сложением МДС отдельных катушек.
где
Физически этот коэффициент характеризует уменьшение МДС катушечной группы с числом витков МДС катушечной группы в любой момент времени и в любой точке, удалённой от оси этой группы на расстояние x можно записать в виде
где МДС фазной обмотки
Пусть на статоре размещена двухслойная обмотка с укороченным шагом и 2р=2 (рис. 1.26). Как показано выше, двухслойная обмотка с укороченным шагом может быть представлена как совокупность двух однослойных обмоток с полным шагом, расположенных в верхнем и нижнем слоях и сдвинутых относительно друг друга на угол укорочения шага (см. рис. 1.26,б).
где Далее можно записать
где
В общем случае, когда машина имеет число полюсов 2р, то фазная обмотка состоит из 2р – катушечных групп, которые можно соединить последовательно, последовательно–параллельно и параллельно. При последовательно-параллельном соединении катушечных групп, число последовательно соединённых витков в фазе будет
где а – число параллельных ветвей;
Тогда или где Для любой
Таким образом, МДС фазной обмотки в любой момент времени и в любой точке сдвинутой относительно оси обмотки на расстояние x будет
Рассмотрим свойства первой гармоники МДС фазы.
Как следует из построения,
При
или
откуда выражение для частоты вращения рассматриваемой прямовращающейся волны получает вид
Путём аналогичного анализа можно доказать, что вторая составляющая
Таким образом, первую гармонику МДС фазной обмотки можно представить в виде двух вращающихся в противоположные стороны с одинаковой частотой вращения волн. При этом амплитуда каждой из них равна половине максимальной амплитуды пульсирующей волны. Для любой
Можно получить тот же вывод методом графического построения. Первую гармонику пульсирующей МДС фазы можно представить в виде пульсирующего пространственного вектора, изменяющегося в пределах
МДС трехфазной обмотки
Трёхфазная обмотка представляет собой совокупность трёх различных обмоток, сдвинутых относительно друг друга на
Каждая из фаз создаёт свою пульсирующую МДС и, следовательно в случае трёхфазной обмотки в воздушном зазоре располагаются три кривых сдвинутых на Рассмотрим первую гармонику. Согласно сказанному выше, значение первой гармоники МДС фаз
В результате первая гармоника МДС трехфазной обмотки
Таким образом, первая гармоника МДС трехфазной обмотки представляет собой прямовращающуюся волну с амплитудой
Если число фаз равно m, то
Этот же вывод следует из графических построений. Удобно первые гармоники МДС отдельных фаз, пульсирующие во времени, представлять в виде пульсирующих пространственных векторов, ориентированных по осям соответствующих фаз. Величина этих векторов пропорциональна мгновенным значениям токов фаз. Для двух моментов времени Мгновенные значения токов определяются, как проекции векторов на вертикаль, которая в данном случае принимается за ось времени. Мгновенные значения токов пропорциональны МДС соответствующих фаз. Выполним графическое построение МДС отдельных фаз и трехфазной обмотки для указанных моментов времени (см. рис. 1.29).
Особо подчеркнем, что при вращении амплитуда первой гармоники результирующей МДС в любой момент времени располагается по оси той фазы, в которой ток максимальный.
МДС двухфазной обмотки
Допустим, что на статоре расположены две обмотки, сдвинутые в пространстве на угол
Рассмотрим моменты времени: Из графического построения (рис. 1.30) следует, что при питании двух фаз, сдвинутых в пространстве на угол
Виды машин переменного тока и их устройство Электрические машины переменного тока включают в себя: 1) синхронные машины (СМ), 2) асинхронные машины (АМ), 3) коллекторные машины переменного тока. Машина переменного тока (МПрТ) состоит из двух основных частей: неподвижной – статора и вращающейся – ротора. Между ними имеется воздушный зазор. Все машины переменного тока работают на принципе вращающегося магнитного поля, поэтому в их теории много общего. В синхронной машине ротор вращается с той же частотой вращения и в том же направлении, что и магнитное поле. То есть в этих машинах ротор и поле вращаются синхронно. В асинхронных машинах ротор вращается с частотой вращения, отличающейся от частоты вращения поля. Другими словами, ротор вращается не синхронно (асинхронно) по отношению к полю. Коллекторные машины являются асинхронными машинами с коллектором. Синхронные машины преимущественно применяются в качестве генераторов, а также нередко – двигателями. Асинхронные машины преимущественно применяются в качестве двигателей. В устройстве статора асинхронной и синхронной машин много общего (рис. 1.1). Сердечник статора набирается из листов электротехнической стали по 0,5 мм, изолированных друг от друга. Сердечник статора запрессовывается в корпус. На внутренней цилиндрической поверхности статора размещены пазы, в которые укладывается распределенная обмотка, как правило, трехфазная. Сердечник ротора асинхронной машины набирается также из листов электротехнической стали, которые в крупных машинах покрываются с обеих сторон масляно-канифольным изоляционным лаком, а в машины малой мощности не имеют лакового покрытия. В последнем случае изоляцией служит искусственно созданный или естественный слой окислов.
а) с фазным ротором или с контактными кольцами (АДФ); б) с короткозамкнутым ротором (АДК). В случае АДФ обмотка ротора выполняется, как и статорная – распределенной. Концы фаз соединяются в общую точку, а начала через контактные кольца и металлографитовые щетки выводятся наружу.
В случае АДК обмотка выполняется в виде беличьей клетки. В каждом пазу укладывается алюминиевый или медный стержень и концы всех стержней с обеих торцов ротора замыкаются накоротко алюминиевыми или медными кольцами. В АМ до 100 кВт обмотка выполняется путем заливки ротора алюминием. Что касается роторов СМ, то их конструкция существенно отличается от конструкции ротора АМ. Существуют две разновидности СМ: |
|
| Поделиться: |

 В СМ это достигается конструктивными мерами. Так воздушный зазор под серединой полюсного наконечника берут меньше зазора под краями (рис. 1.5). Тем не менее, кривая поля в воздушном зазоре содержит, как правило, кроме первой высшие гармоники. Определим ЭДС обмотки от первой гармоники поля.
В СМ это достигается конструктивными мерами. Так воздушный зазор под серединой полюсного наконечника берут меньше зазора под краями (рис. 1.5). Тем не менее, кривая поля в воздушном зазоре содержит, как правило, кроме первой высшие гармоники. Определим ЭДС обмотки от первой гармоники поля.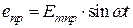 ,
,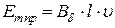 .
.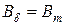 – максимальное значение индукции в воздушном зазоре от первой гармоники поля;
– максимальное значение индукции в воздушном зазоре от первой гармоники поля;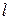 – активная длина проводника;
– активная длина проводника;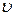 – окружная скорость поля, причем
– окружная скорость поля, причем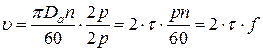 ,
,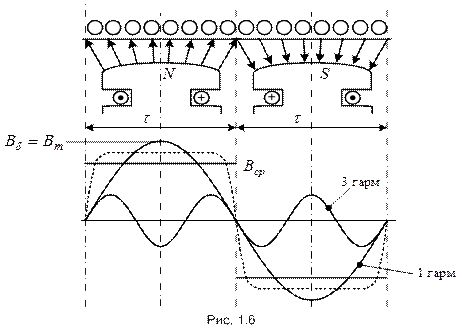
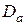 – диаметр расточки якоря,
– диаметр расточки якоря,  – полюсное деление,
– полюсное деление,  – число пар полюсов,
– число пар полюсов, 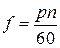 – частота ЭДС.
– частота ЭДС.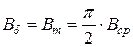 – максимальное значение индукции;
– максимальное значение индукции;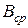 – среднее значение индукции.
– среднее значение индукции.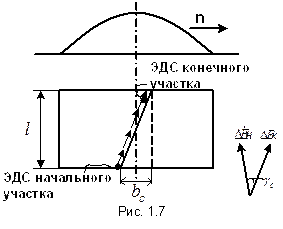
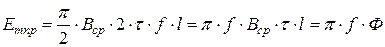 ,
,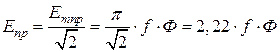 .
. ,
,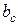 – расстояние между началом и концом проводника (рис. 1.7).
– расстояние между началом и концом проводника (рис. 1.7). и их можно представить в виде векторов, сдвинутых на указанный угол.
и их можно представить в виде векторов, сдвинутых на указанный угол.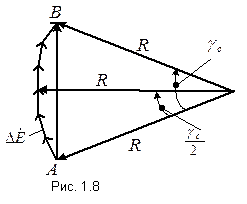 Непосредственно из построения (рис. 1.8) коэффициент скоса
Непосредственно из построения (рис. 1.8) коэффициент скоса 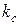 и ЭДС проводника с учетом скоса можно представить в следующем виде:
и ЭДС проводника с учетом скоса можно представить в следующем виде: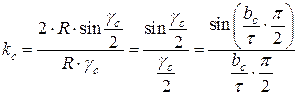 ;
;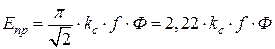 .
. ) ЭДС проводников, составляющих виток сдвинуты на угол π:
) ЭДС проводников, составляющих виток сдвинуты на угол π: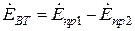 .
.
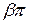 , где
, где 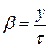 – относительный угловой шаг обмотки.
– относительный угловой шаг обмотки.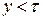 ) уменьшается по сравнению с ЭДС витка с полным шагом (рис. 1.10)
) уменьшается по сравнению с ЭДС витка с полным шагом (рис. 1.10)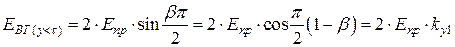 .
.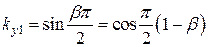 – коэффициент укорочения по первой гармонике.
– коэффициент укорочения по первой гармонике.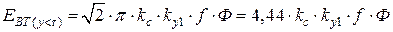 .
.
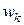 . ЭДС катушки можно записать с учетом скоса и укорочения:
. ЭДС катушки можно записать с учетом скоса и укорочения: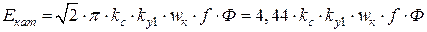 .
.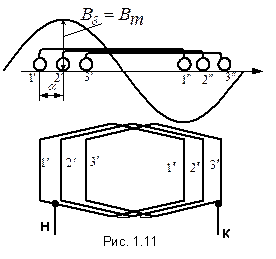 Допустим
Допустим 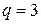 (рис. 1.11). Угол между соседними пазами:
(рис. 1.11). Угол между соседними пазами: 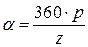 – эл. град или
– эл. град или  – эл. рад, где z – число пазов статора (якоря).
– эл. рад, где z – число пазов статора (якоря).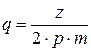 .
. , соответствующий пространственному углу
, соответствующий пространственному углу 
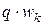 витков, распределенных в q пазах по сравнению с ЭДС тех же витков, расположенных в одном пазу. Определим коэффициент распределения из графического построения (рис. 1.13):
витков, распределенных в q пазах по сравнению с ЭДС тех же витков, расположенных в одном пазу. Определим коэффициент распределения из графического построения (рис. 1.13): .
.
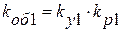 – обмоточный коэффициент по первой гармонике.
– обмоточный коэффициент по первой гармонике.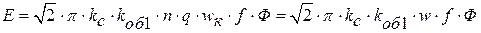 .
.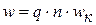 – число последовательно соединенных витков фазы.
– число последовательно соединенных витков фазы. – шагу обмотки. Совокупность нескольких последовательно соединенных витков образуют катушку или секцию. Нередко катушкой называют несколько секций, объединенных общей изоляцией. В машинах переменного тока применяются катушечные и стержневые обмотки, петлевые и волновые.
– шагу обмотки. Совокупность нескольких последовательно соединенных витков образуют катушку или секцию. Нередко катушкой называют несколько секций, объединенных общей изоляцией. В машинах переменного тока применяются катушечные и стержневые обмотки, петлевые и волновые.
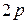 – число плюсов; m – число фаз; y – шаг обмотки;
– число плюсов; m – число фаз; y – шаг обмотки;  – число пазов на полюс и фазу.
– число пазов на полюс и фазу.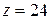 ;
;  ;
;  ;
; 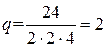 ;
;  (рис. 1.16).
(рис. 1.16).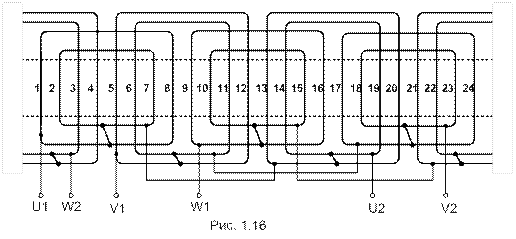
 , N=8
, N=8 или дробное число
или дробное число  В общем случае, когда машина имеет 2р полюсов, каждая из фаз будет состоять из 2р катушечных групп, которые можно соединить последовательно, последовательно-параллельно и параллельно. Максимальное число параллельных ветвей фазы
В общем случае, когда машина имеет 2р полюсов, каждая из фаз будет состоять из 2р катушечных групп, которые можно соединить последовательно, последовательно-параллельно и параллельно. Максимальное число параллельных ветвей фазы 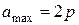 .
.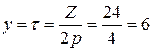 ;
;  .
.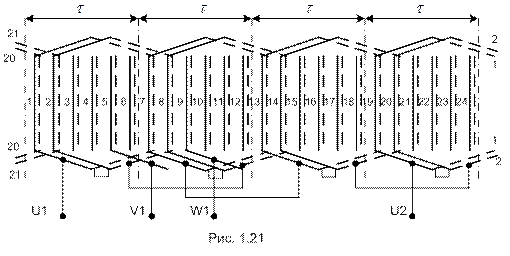
 , что соответствует 4 пазам. Катушечная группа в пределах фазной обмотки могут соединяться последовательно (см. рис. 1.21), а также последовательно-параллельно и параллельно.
, что соответствует 4 пазам. Катушечная группа в пределах фазной обмотки могут соединяться последовательно (см. рис. 1.21), а также последовательно-параллельно и параллельно. , где а – число параллельных ветвей. Максимальное число параллельных ветвей будет в том случае, когда все катушечные группы соединены параллельно (
, где а – число параллельных ветвей. Максимальное число параллельных ветвей будет в том случае, когда все катушечные группы соединены параллельно ( ;
;  ;
;  .
.
 . Эти обмотки применяются также для роторов асинхронных машин с контактными кольцами.
. Эти обмотки применяются также для роторов асинхронных машин с контактными кольцами. ;
; 
 принимается бесконечной;
принимается бесконечной;
 .
. .
. , то можно пренебречь падением магнитного потенциала на стальных участках и считать, что вся МДС идёт на проведение потока через воздушный зазор:
, то можно пренебречь падением магнитного потенциала на стальных участках и считать, что вся МДС идёт на проведение потока через воздушный зазор: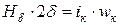
 .
. .
. – удельная магнитная проводимость воздушного зазора;
– удельная магнитная проводимость воздушного зазора; – МДС на полюс,
– МДС на полюс, ,
, – максимальная амплитуда пульсации МДС.
– максимальная амплитуда пульсации МДС.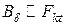 . Следовательно, кривая
. Следовательно, кривая  аналогична кривой МДС. Поэтому определение индукции
аналогична кривой МДС. Поэтому определение индукции  ,
, .
. , то
, то ,
, – максимальная амплитуда пульсаций первой гармоники МДС.
– максимальная амплитуда пульсаций первой гармоники МДС. ,
, – максимальная амплитуда пульсаций
– максимальная амплитуда пульсаций  -той гармоники МДС.
-той гармоники МДС. . Там изображены первые гармоники катушек и катушечной группы.
. Там изображены первые гармоники катушек и катушечной группы.
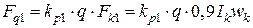 ,
, – коэффициент распределения для первой гармоники.
– коэффициент распределения для первой гармоники.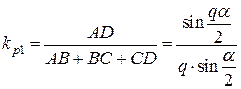 .
. ,
, .
. . Такой подход в данном случае вполне обоснован, так как величина МДС не зависит от порядка соединения проводников, а зависит от тока в проводниках и их размещения. В результате любую гармонику МДС двухслойной обмотки с укороченным шагом можно получить путём сложения соответствующих гармоник МДС воображаемых однослойных обмоток. При этом МДС катушечных групп, лежащих в верхнем и нижнем слоях, можно представить в виде пространственных векторов, сдвинутых на угол
. Такой подход в данном случае вполне обоснован, так как величина МДС не зависит от порядка соединения проводников, а зависит от тока в проводниках и их размещения. В результате любую гармонику МДС двухслойной обмотки с укороченным шагом можно получить путём сложения соответствующих гармоник МДС воображаемых однослойных обмоток. При этом МДС катушечных групп, лежащих в верхнем и нижнем слоях, можно представить в виде пространственных векторов, сдвинутых на угол  , определяемый укорочением шага. На рис. 1.26,а показано построение первых гармоник МДС катушечных групп и фазной обмотки при
, определяемый укорочением шага. На рис. 1.26,а показано построение первых гармоник МДС катушечных групп и фазной обмотки при 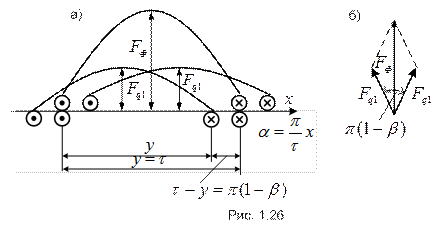
 ,
, – коэффициент укорочения для первой гармоники.
– коэффициент укорочения для первой гармоники. ,
, – обмоточный коэффициент.
– обмоточный коэффициент. .
. ,
, .
.
 ,
, – ток фазной обмотки.
– ток фазной обмотки. .
. .
.
 Изобразим первую составляющую
Изобразим первую составляющую  для двух моментов времени:
для двух моментов времени:  и
и  (рис. 1.27).
(рис. 1.27).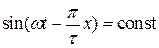 или
или 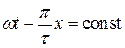 .
.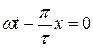 ,
,  и
и
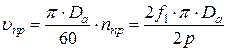 ,
, .
.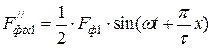 – является обратновращающейся волной
– является обратновращающейся волной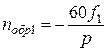 .
. ;
; ,
,  .
. . Такой вектора можно заменить двумя вращающимися векторами. Построим эти векторы для моментов времени
. Такой вектора можно заменить двумя вращающимися векторами. Построим эти векторы для моментов времени  ;
;  ;
;  (рис. 1.28)
(рис. 1.28)
 эл. радиан. При симметричной нагрузке в фазных обмотках будут протекать токи, сдвинутые во времени на
эл. радиан. При симметричной нагрузке в фазных обмотках будут протекать токи, сдвинутые во времени на  ;
; ;
;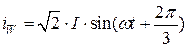 .
. в любой момент времени и в любой точке зазора, сдвинутой относительно оси фазы
в любой момент времени и в любой точке зазора, сдвинутой относительно оси фазы  , можно представить соответственно:
, можно представить соответственно:


 .
. .
. .
. – синхронная частота вращения.
– синхронная частота вращения.
 и
и  построим векторные диаграммы токов (рис. 1.29,а,в).
построим векторные диаграммы токов (рис. 1.29,а,в). Таким образом, как следует из построения, складывая первые гармоники пульсирующих МДС отдельных фаз в разные моменты времени, получаем пространственный результирующий вектор, изображающий первую гармонику МДС трехфазной обмотки, вращающуюся в определенном направлении
Таким образом, как следует из построения, складывая первые гармоники пульсирующих МДС отдельных фаз в разные моменты времени, получаем пространственный результирующий вектор, изображающий первую гармонику МДС трехфазной обмотки, вращающуюся в определенном направлении  . При этом амплитуда этой гармоники
. При этом амплитуда этой гармоники  и
и 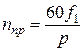 .
. (обмотки
(обмотки 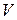 ). В этих обмотках протекают одинаковые токи, сдвинутые по фазе на тот же угол. Допустим, что ток фазы
). В этих обмотках протекают одинаковые токи, сдвинутые по фазе на тот же угол. Допустим, что ток фазы  ,
,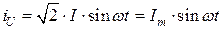 .
. ,
, 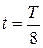 ,
,  и имеющая амплитуду
и имеющая амплитуду 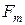 (речь идет об первой гармонике МДС).
(речь идет об первой гармонике МДС).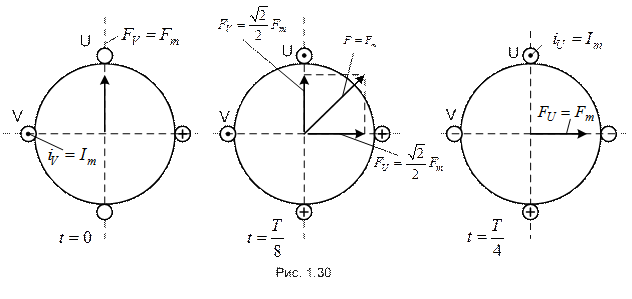
 Пакет листов ротора АМ напрессовывается на вал (рис. 1.2,а) или на втулку вала. В крупных АМ он напрессовывается на крестовину (обод) (рис. 1.2,б). В пазах на наружной поверхности пакета ротора укладывается обмотка ротора. В зависимости от типа обмотки различают два различных типа АМ:
Пакет листов ротора АМ напрессовывается на вал (рис. 1.2,а) или на втулку вала. В крупных АМ он напрессовывается на крестовину (обод) (рис. 1.2,б). В пазах на наружной поверхности пакета ротора укладывается обмотка ротора. В зависимости от типа обмотки различают два различных типа АМ:



