
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ЭДС обмоток переменного токаСодержание книги Поиск на нашем сайте
При проектировании МПрТ стремятся к такому, чтобы их ЭДС имела синусоидальную форму. В машинах, в которых ЭДС наводится в обмотках, вращающимся полем индуктора, форма кривой ЭДС зависит от распределения индукции в воздушном зазоре. Чтобы обеспечить синусоидальную форму ЭДС, надо приблизить распределение индукции в воздушном зазоре к синусоидальному.
ЭДС проводника, витка и катушки
Вопросы наведения ЭДС в обмотке переменного тока удобно рассматривать на примере СМ. С этой целью удобно часть машины, соответствующую двойному полюсному делению изобразить в развернутом виде (рис.1.6). При вращении индуктора первая гармоника индуктирует в каждом из проводников ЭДС
где
Здесь
где На рис. 1.6 указаны следующие обозначения:
Следовательно, максимальное и действующее значения ЭДС проводника будут:
Нередко в машинах выполняют пазы со скосом по длине. В этом случае начало и конец проводника оказываются сдвинутыми относительно друг друга на угол γ
где Можно разбить проводник на малые участки по длине. В разное время эти участки будут находится под различным воздействием поля. Следовательно, ЭДС этих участков будут сдвинуты во времени относительно друг друга. Так, например, ЭДС начального и конечного участка будут сдвинуты на угол ЭДС всего проводника в данном случае будет равна геометрической сумме ЭДС отдельных участков, причем сумма геометрическая меньше суммы арифметической. Уменьшение ЭДС проводника при наличии скоса пазов характеризуется коэффициентом скоса. Если участки принять бесконечно малыми, то геометрическая сумма их ЭДС изобразится дугой, а ее величина – хордой дуги, опирающейся на угол
Определим ЭДС витка. Виток – совокупность двух последовательно соединенных проводников, расположенных на расстоянии равном или близком к полюсному делению. Шаг витка обозначается у (рис. 1.9). При диаметральном или полном шаге витка (
ЭДС проводников можно изобразить в виде противоположно направленных векторов. Величина ЭДС витка в данном случае
В машинах переменного тока часто прибегают к укорочению шага (см. рис. 1.9). В этом случае ЭДС проводников, составляющих виток, будут сдвинуты не на π, а на угол Величина ЭДС витка с укороченным шагом (
Здесь Окончательно
Обмотки, как правило, выполняются из катушек. Катушка – совокупность нескольких последовательно соединенных витков
ЭДС катушечной группы
Обмотки машин переменного тока, как правило, выполняются из катушечных групп. Катушечная группа – это совокупность q последовательно соединенных катушек, катушечные стороны которых расположены в q соседних пазах.
Угол, который соответствует катушечной группе в пределах одного или двух полюсных делений, называют углом фазной зоны. В машинах переменного тока применяют симметричные трехфазные обмотки шестизонные и трехзонные. В первом случае угол фазной зоны 60˚, во втором случае угол фазной зоны 120˚. В случае шестизонной обмотки в пределах каждого полюсного деления размещаются три фазы, при этом на каждую фазу приходится одинаковое число пазов
При вращении первая гармоника поля наводит в катушках ЭДС, сдвинутые во времени по фазе на угол
Для определения ЭДС катушечной группы следует геометрически сложить ЭДС отдельных катушек. При этом сумма геометрическая меньше суммы арифметической ЭДС катушек. Отношение величины геометрической суммы к сумме арифметической – коэффициент распределения. Он характеризует уменьшение ЭДС катушечной группы из
В результате ЭДС катушечной группы с учетом скоса, укорочения и распределения
Здесь Фазная обмотка обычно состоит из нескольких катушечных групп, соединенных последовательно, последовательно–параллельно или параллельно. ЭДС фазы равна ЭДС параллельной ветви. Если в этой параллельной ветви имеется n последовательно соединенных катушечных групп, то
Здесь
|
||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 340; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.134.165 (0.01 с.) |

 В СМ это достигается конструктивными мерами. Так воздушный зазор под серединой полюсного наконечника берут меньше зазора под краями (рис. 1.5). Тем не менее, кривая поля в воздушном зазоре содержит, как правило, кроме первой высшие гармоники. Определим ЭДС обмотки от первой гармоники поля.
В СМ это достигается конструктивными мерами. Так воздушный зазор под серединой полюсного наконечника берут меньше зазора под краями (рис. 1.5). Тем не менее, кривая поля в воздушном зазоре содержит, как правило, кроме первой высшие гармоники. Определим ЭДС обмотки от первой гармоники поля.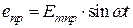 ,
,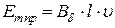 .
. – максимальное значение индукции в воздушном зазоре от первой гармоники поля;
– максимальное значение индукции в воздушном зазоре от первой гармоники поля; – активная длина проводника;
– активная длина проводника;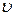 – окружная скорость поля, причем
– окружная скорость поля, причем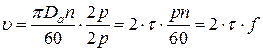 ,
,
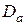 – диаметр расточки якоря,
– диаметр расточки якоря,  – полюсное деление,
– полюсное деление,  – число пар полюсов,
– число пар полюсов, 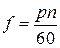 – частота ЭДС.
– частота ЭДС.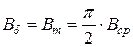 – максимальное значение индукции;
– максимальное значение индукции; – среднее значение индукции.
– среднее значение индукции.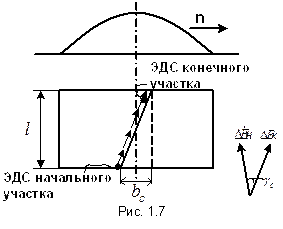
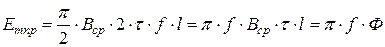 ,
,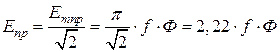 .
. ,
, – расстояние между началом и концом проводника (рис. 1.7).
– расстояние между началом и концом проводника (рис. 1.7). и их можно представить в виде векторов, сдвинутых на указанный угол.
и их можно представить в виде векторов, сдвинутых на указанный угол.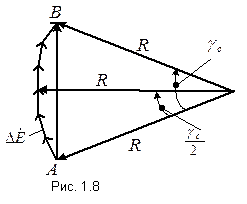 Непосредственно из построения (рис. 1.8) коэффициент скоса
Непосредственно из построения (рис. 1.8) коэффициент скоса 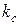 и ЭДС проводника с учетом скоса можно представить в следующем виде:
и ЭДС проводника с учетом скоса можно представить в следующем виде: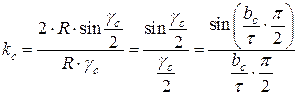 ;
;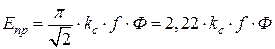 .
. ) ЭДС проводников, составляющих виток сдвинуты на угол π:
) ЭДС проводников, составляющих виток сдвинуты на угол π: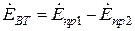 .
.
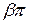 , где
, где 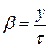 – относительный угловой шаг обмотки.
– относительный угловой шаг обмотки.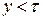 ) уменьшается по сравнению с ЭДС витка с полным шагом (рис. 1.10)
) уменьшается по сравнению с ЭДС витка с полным шагом (рис. 1.10)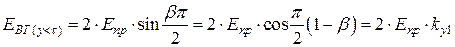 .
.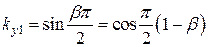 – коэффициент укорочения по первой гармонике.
– коэффициент укорочения по первой гармонике.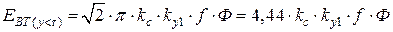 .
.
 . ЭДС катушки можно записать с учетом скоса и укорочения:
. ЭДС катушки можно записать с учетом скоса и укорочения: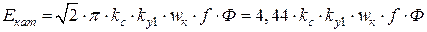 .
.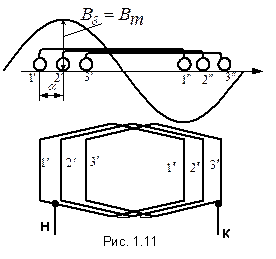 Допустим
Допустим 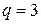 (рис. 1.11). Угол между соседними пазами:
(рис. 1.11). Угол между соседними пазами: 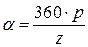 – эл. град или
– эл. град или  – эл. рад, где z – число пазов статора (якоря).
– эл. рад, где z – число пазов статора (якоря).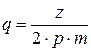 .
. , соответствующий пространственному углу
, соответствующий пространственному углу 
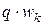 витков, распределенных в q пазах по сравнению с ЭДС тех же витков, расположенных в одном пазу. Определим коэффициент распределения из графического построения (рис. 1.13):
витков, распределенных в q пазах по сравнению с ЭДС тех же витков, расположенных в одном пазу. Определим коэффициент распределения из графического построения (рис. 1.13): .
.
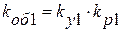 – обмоточный коэффициент по первой гармонике.
– обмоточный коэффициент по первой гармонике.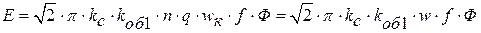 .
.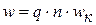 – число последовательно соединенных витков фазы.
– число последовательно соединенных витков фазы.


