
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
МДС обмоток переменного тока и катушкиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
МДС катушки
При изучении МДС обмоток переменного тока делаются следующие допущения: а) магнитная проницаемость стальных участков магнитопровода б) выступающие полюса и паза отсутствуют и зазор равномерен; в) катушечные стороны обмотки расположены непосредственно в воздушном зазоре и в сечении имеют вид тонких лент с шириной δ; г) воздушный зазор очень мал по сравнению с радиусом расточки статора и величиной полюсного деления. Указанные допущения наиболее близки в действительности в АМ, у которых, расточка статора и ротор имеют цилиндрическую форму. Пусть на статоре АМ размещена простейшая обмотка с полным шагом
Катушечный ток При протекании тока, катушка создаёт пульсирующее магнитное поле. МДС действующая по каждому из контуров 1,2 и т.д. может быть определена по закону полного тока:
Так как согласно первому допущению
или
Здесь
причем Отметим, что МДС катушки пульсирует во времени по закону синуса, причем
где
Так как
где Тогда где Таким образом, МДС катушки в любой момент времени и в любой точке пространства, удалённой на расстояние x от оси катушки, может быть представлена как сумма основной и высших пространственных гармоник, пульсирующих во времени по закону синуса с одинаковой частотой.
МДС катушечной группы
Как известно, катушечная группа представляет собой совокупность последовательно соединённых q катушек, катушечные стороны которых в пределах полюсного деления размещены в соседних пазах. При
Указанные гармоники МДС катушек можно представить в виде пространственных векторов, сдвинутых на угол α (рис. 1.25,б). Максимальная амплитуда первой гармоники МДС катушечной группы может быть получена геометрическим сложением МДС отдельных катушек.
где
Физически этот коэффициент характеризует уменьшение МДС катушечной группы с числом витков МДС катушечной группы в любой момент времени и в любой точке, удалённой от оси этой группы на расстояние x можно записать в виде
где МДС фазной обмотки
Пусть на статоре размещена двухслойная обмотка с укороченным шагом и 2р=2 (рис. 1.26). Как показано выше, двухслойная обмотка с укороченным шагом может быть представлена как совокупность двух однослойных обмоток с полным шагом, расположенных в верхнем и нижнем слоях и сдвинутых относительно друг друга на угол укорочения шага
(см. рис. 1.26,б).
где Далее можно записать
где
В общем случае, когда машина имеет число полюсов 2р, то фазная обмотка состоит из 2р – катушечных групп, которые можно соединить последовательно, последовательно–параллельно и параллельно. При последовательно-параллельном соединении катушечных групп, число последовательно соединённых витков в фазе будет
где а – число параллельных ветвей;
Тогда или где Для любой
Таким образом, МДС фазной обмотки в любой момент времени и в любой точке сдвинутой относительно оси обмотки на расстояние x будет
Рассмотрим свойства первой гармоники МДС фазы.
Как следует из построения,
При
или
откуда выражение для частоты вращения рассматриваемой прямовращающейся волны получает вид
Путём аналогичного анализа можно доказать, что вторая составляющая
Таким образом, первую гармонику МДС фазной обмотки можно представить в виде двух вращающихся в противоположные стороны с одинаковой частотой вращения волн. При этом амплитуда каждой из них равна половине максимальной амплитуды пульсирующей волны. Для любой
Можно получить тот же вывод методом графического построения. Первую гармонику пульсирующей МДС фазы можно представить в виде пульсирующего пространственного вектора, изменяющегося в пределах
МДС трехфазной обмотки
Трёхфазная обмотка представляет собой совокупность трёх различных обмоток, сдвинутых относительно друг друга на
Каждая из фаз создаёт свою пульсирующую МДС и, следовательно в случае трёхфазной обмотки в воздушном зазоре располагаются три кривых сдвинутых на Рассмотрим первую гармонику. Согласно сказанному выше, значение первой гармоники МДС фаз
В результате первая гармоника МДС трехфазной обмотки
Таким образом, первая гармоника МДС трехфазной обмотки представляет собой прямовращающуюся волну с амплитудой
Если число фаз равно m, то
Этот же вывод следует из графических построений. Удобно первые гармоники МДС отдельных фаз, пульсирующие во времени, представлять в виде пульсирующих пространственных векторов, ориентированных по осям соответствующих фаз. Величина этих векторов пропорциональна мгновенным значениям токов фаз. Для двух моментов времени Мгновенные значения токов определяются, как проекции векторов на вертикаль, которая в данном случае принимается за ось времени. Мгновенные значения токов пропорциональны МДС соответствующих фаз. Выполним графическое построение МДС отдельных фаз и трехфазной обмотки для указанных моментов времени (см. рис. 1.29).
Особо подчеркнем, что при вращении амплитуда первой гармоники результирующей МДС в любой момент времени располагается по оси той фазы, в которой ток максимальный.
|
|||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 770; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.226.195 (0.012 с.) |

 принимается бесконечной;
принимается бесконечной; и имеющая
и имеющая 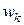 витков (рис. 1.24).
витков (рис. 1.24).
 .
. .
. , то можно пренебречь падением магнитного потенциала на стальных участках и считать, что вся МДС идёт на проведение потока через воздушный зазор:
, то можно пренебречь падением магнитного потенциала на стальных участках и считать, что вся МДС идёт на проведение потока через воздушный зазор: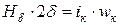
 .
. .
. – удельная магнитная проводимость воздушного зазора;
– удельная магнитная проводимость воздушного зазора; – МДС на полюс,
– МДС на полюс, ,
, – максимальная амплитуда пульсации МДС.
– максимальная амплитуда пульсации МДС.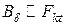 . Следовательно, кривая
. Следовательно, кривая  аналогична кривой МДС. Поэтому определение индукции
аналогична кривой МДС. Поэтому определение индукции  ,
, .
. , то
, то ,
, – максимальная амплитуда пульсаций первой гармоники МДС.
– максимальная амплитуда пульсаций первой гармоники МДС. ,
, – максимальная амплитуда пульсаций
– максимальная амплитуда пульсаций  -той гармоники МДС.
-той гармоники МДС.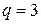 (рис. 1.25) МДС катушки в пределах полюсного деления имеет вид прямоугольника и следовательно, в данном случае будем иметь три прямоугольника, сдвинутых относительно друг друга на угол
(рис. 1.25) МДС катушки в пределах полюсного деления имеет вид прямоугольника и следовательно, в данном случае будем иметь три прямоугольника, сдвинутых относительно друг друга на угол  . В результате МДС катушечной группы можно получить путём сложения ординат прямоугольников. Однако обычно каждый из прямоугольников разлагают в ряд Фурье и сложением МДС катушек одного порядка определяют соответствующие гармоники МДС катушечной группы. Сделаем это для первой гармоники МДС. На рис.1.25,а изображен случай, когда
. В результате МДС катушечной группы можно получить путём сложения ординат прямоугольников. Однако обычно каждый из прямоугольников разлагают в ряд Фурье и сложением МДС катушек одного порядка определяют соответствующие гармоники МДС катушечной группы. Сделаем это для первой гармоники МДС. На рис.1.25,а изображен случай, когда  . Там изображены первые гармоники катушек и катушечной группы.
. Там изображены первые гармоники катушек и катушечной группы.
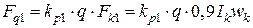 ,
, – коэффициент распределения для первой гармоники.
– коэффициент распределения для первой гармоники.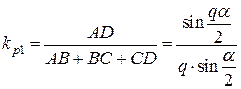 .
.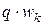 , по сравнению с МДС катушки с тем же числом витков.
, по сравнению с МДС катушки с тем же числом витков. ,
, .
. . Такой подход в данном случае вполне обоснован, так как величина МДС не зависит от порядка соединения проводников, а зависит от тока в проводниках и их размещения. В результате любую гармонику МДС двухслойной обмотки с укороченным шагом можно получить путём сложения соответствующих гармоник МДС воображаемых однослойных обмоток. При этом МДС катушечных групп, лежащих в верхнем и нижнем слоях, можно представить в виде пространственных векторов, сдвинутых на угол
. Такой подход в данном случае вполне обоснован, так как величина МДС не зависит от порядка соединения проводников, а зависит от тока в проводниках и их размещения. В результате любую гармонику МДС двухслойной обмотки с укороченным шагом можно получить путём сложения соответствующих гармоник МДС воображаемых однослойных обмоток. При этом МДС катушечных групп, лежащих в верхнем и нижнем слоях, можно представить в виде пространственных векторов, сдвинутых на угол  , определяемый укорочением шага. На рис. 1.26,а показано построение первых гармоник МДС катушечных групп и фазной обмотки при
, определяемый укорочением шага. На рис. 1.26,а показано построение первых гармоник МДС катушечных групп и фазной обмотки при 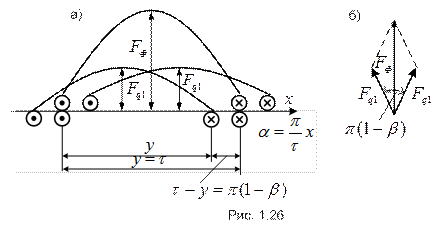
 ,
, – коэффициент укорочения для первой гармоники.
– коэффициент укорочения для первой гармоники. ,
, – обмоточный коэффициент.
– обмоточный коэффициент. .
. ,
, .
.
 ,
, – ток фазной обмотки.
– ток фазной обмотки. .
. .
.
 Изобразим первую составляющую
Изобразим первую составляющую  для двух моментов времени:
для двух моментов времени:  и
и  (рис. 1.27).
(рис. 1.27).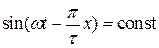 или
или 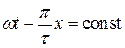 .
.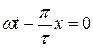 ,
,  и
и
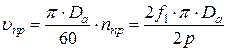 ,
, .
.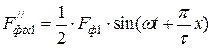 – является обратновращающейся волной
– является обратновращающейся волной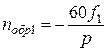 .
. ;
; ,
,  .
. . Такой вектора можно заменить двумя вращающимися векторами. Построим эти векторы для моментов времени
. Такой вектора можно заменить двумя вращающимися векторами. Построим эти векторы для моментов времени  ;
;  ;
;  (рис. 1.28)
(рис. 1.28)
 эл. радиан. При симметричной нагрузке в фазных обмотках будут протекать токи, сдвинутые во времени на
эл. радиан. При симметричной нагрузке в фазных обмотках будут протекать токи, сдвинутые во времени на  ;
; ;
;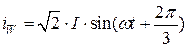 .
. в любой момент времени и в любой точке зазора, сдвинутой относительно оси фазы
в любой момент времени и в любой точке зазора, сдвинутой относительно оси фазы  , можно представить соответственно:
, можно представить соответственно:


 .
. .
. .
. – синхронная частота вращения.
– синхронная частота вращения.
 и
и  построим векторные диаграммы токов (рис. 1.29,а,в).
построим векторные диаграммы токов (рис. 1.29,а,в). Таким образом, как следует из построения, складывая первые гармоники пульсирующих МДС отдельных фаз в разные моменты времени, получаем пространственный результирующий вектор, изображающий первую гармонику МДС трехфазной обмотки, вращающуюся в определенном направлении
Таким образом, как следует из построения, складывая первые гармоники пульсирующих МДС отдельных фаз в разные моменты времени, получаем пространственный результирующий вектор, изображающий первую гармонику МДС трехфазной обмотки, вращающуюся в определенном направлении  . При этом амплитуда этой гармоники
. При этом амплитуда этой гармоники  и
и 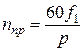 .
.


