
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Результаты измерений с помощью измерителя добротности и вычисления параметров катушки индуктивностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Таблица 5.3. Результаты измерения с помощью измерителя добротности и вычисления параметров конденсатора и резистора
Таблица 5.4. Результаты измерения L, C, R, измерителем добротности и оценки их основной абсолютной и относительной неопределенностей
5.7. Вычислить полное сопротивление катушки индуктивности, конденсатора и резистора. Z=R+jx. 5.8. Оформите результаты измерений в соответствии с нормативными документами. Проанализируйте полученные результаты и сделайте выводы в письменной форме. СОДЕРЖАНИЕ ОТЧЕТА
6.1. Отчет по лабораторной работе должен быть оформлен в соответствии с СТП НЭИС-01.07.86. 6.2. Отчет должен содержать: 1) титульный лист; 2) формулировку цели работы; 3) задание к лабораторной работе; 4) метрологические характеристики средств измерений, оформленные в таблицу; 5) решение задач, предложенных в методических указаниях к лабораторной работе; 6) схемы измерений по каждому пункту программы лабораторной работы, оформленные в соответствии с требованиями ГОСТов группы Т52; 7) расчетные формулы по обработке результатов наблюдений и измерений, в том числе формулы по оценке неопределенностей измерений по каждому пункту программы лабораторной работы; 8) результаты экспериментальных исследований по каждому пункту лабораторной работы, оформленные в заготовленных таблицах в соответствии с нормативной документацией; 9) выводы по каждому эксперименту и по работе в целом.
ЛИТЕРАТУРА
1. Метрология, стандартизация и измерения в технике связи: Учеб. пособие для вузов/ Б.П. Хромой, А.В. Кандинов, А.Л. Синявский и др.:Под ред. Б.П. Хромого.-М: Радио и связь, 1986-424 с.:ил.
2. Мирский Г.Я. Электронные измерения: 4-е изд. перераб. и доп. –М.: Радио и связь,1986-440 с.:ил. 3. Кушнир Ф.В. Электрорадиоизмерения: Учебное пособие для вузов.- Л. Энергоатомиздат. Ленингр. отд-ние, 1983-320 с.: ил. 4. Оценка погрешности результатов измерений при выполнении лабораторных работ: Методические указания/ Н.И. Горлов, И.Н. Запасный, В.И. Сметанин, Г.Д. Созонник - Новосибирск-Киев, 1989.-29 с.:ил. 5. Методические указания по применению измерительных приборов и макетов в лабораторном практикуме курса метрология, стандартизация и управление качеством / А.Б. Гоникман, Н.И. Горлов, И.Н. Запасный, В.И. Сметанин, Ю.А. Пальчун - Новосибирск, 1991.-78 с.:ил. 6. Оценка неопределенности измерений при экспериментальных исследованиях. Учебное пособие / Н.И. Горлов, И.Н. Запасный, Ю.А. Пальчун, В.И. Сметанин и др. – Новосибирск: СибГУТИ, 2001. – 60 с.
ПРИЛОЖЕНИЯ
ОЦЕНКА ОСНОВНОЙ АБСОЛЮТНОЙ НЕОПРЕДЕЛЕННОСТИ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ДВУХПОЛЮСНИКОВ Оценку основной абсолютной неопределенности как мостовым, так и резонансным методами осуществляют по метрологическим характеристикам, указанным в паспорте прибора. Если класс точности прибора установлен по относительной неопределенности измерения параметра, то оценка основной абсолютной неопределенности оценивается по формуле
где: d - относительная неопределенность измерения соответствующего параметра, % Ах - измеренное значение параметра. Оценку неопределенностей измерений с помощью измерителя добротности следует проводить по методике косвенных измерений [4], с 23-28.
ИЗМЕРЕНИЕ ПАРАМЕТРОВ ДВУХПОЛЮСНИКОВ РЕЗОНАНСНЫМ МЕТОДОМ С ПОМОЩЬЮ ИЗМЕРИТЕЛЯ ДОБРОТНОСТИ (КУМЕТРОМ)
8.2.1. Обшее положение. Резонансный метод измерения сводится к определению степени влияния исследуемого двухполюсника на параметры образцового измерительного контура в момент настройки в резонанс. Для измерения параметров двухполюсников резонансным методом применяют измерительные приборы – измерители добротности (куметры). Структурная схема измерителя добротности состоит из: генератора высокой частоты; последовательного измерительного контура; индикатора резонанса V2 (рис. 8.1.). Генератор снабжон градуировочной шкалой для установки частоты, на которой производят измерение. Измерительный контур состоит из исследуемой или вспомогательной катушки индуктивности L и
Рис. 8.1. Схема измерителя добротности.
образцового конденсатора переменной емкости Собр. В качестве индикатора резонанса обычно применяют встроенный электронный вольтметр (V2). В измерительный контур через развязывающее устройство (на схеме рис. 8.1. не показано) вводят напряжение Ео, равное обычно 50 мВ. Значение этого напряжения контролирует вольтметр V1. Электронный вольтметр V2. служит индикатором резонанса в последовательном LСобр -контуре, при котором напряжение на реактивном элементе (в нашем случае на конденсаторе Собр, U2) в Q раз больше напряжения U1, подведенного к контуру при резонансе, т.е. Q=U2/ U1. Если напряжение U1 поддерживать постоянным, то вольтметр V2, измеряющий напряжение U2, может быть проградуирован непосредственно в значениях добротности Q. Куметр снабжен комплектом вспомогательных катушек индуктивности, подключаемых к зажимам 1-4 (Lх). На рис. 8.1. показано вспомогательное устройство, позволяющее к зажимам 1-4 (Lх) последовательно подключить вспомогательную катушку L (зажимы 1-2) и исследуемый двухполюсник (зажимы 3-4). Зажимы 4-5 (Сх) используют для подключения исследуемого двухполюсника параллельно образцовому конденсатору Собр. Куметр находит широкое применение для измерения полных сопротивлений и других параметров цепей: индуктивностей, емкостей, резистивных сопротивлений, добротностей, тангенса угла потерь, как цепей с сосредоточенными, так и с рассредоточенными постоянными. Он дает возможность довольно просто измерить практически любые сопротивления в области высоких и сверхвысоких частот, где измерение их другими способами затруднительно.
8.2.2. Измерение полных сопротивлений. О размере сопротивления можно судить по реакции настроенного в резонанс контура. При малом значении модуля полного сопротивления исследуемый объект включают последовательно с LСобр контуром. При этом к зажимам «Lx» куметра подключают последовательно соединенный измеряемый объект (зажимы 3-4). и вспомогательную катушку индуктивности (зажимы 1-2). При большом значении модуля полного сопротивления исследуемый объект подключают параллельно конденсатору контура - к зажимам 4-5 «CX» измерителя добротности. Если величина модуля исследуемого объекта неизвестна, необходимо опробовать обе схемы включения и выбрать схему, при которой добротность измерительного конура выше.
Процесс измерения параметров двухполюсника состоит из двух этапов. 1 этап. Измеряют параметры образцового резонансного контура, состоящего из встроенного в прибор образцового конденсатора и вспомогательной сменной катушки (рис. 5.1.). Вспомогательную катушку выбирают таким образом, чтобы в диапазон частот, указанный на вспомогательной катушке попадала частота, на которой будут выполнять измерения.Настроив на заданной частоте образцовый контур в резонанс путем изменения образцовой емкости Собр, снимают показания добротности и образцовой емкости, которые обозначим через Q 1 и С 1. 2 этап. В зависимости от размера модуля сопротивления, исследуемый объект включают параллельно (рис. 5.4.) или последовательно (рис. 5.5.) в образцовый контур. После этого, производят настройку образованного контура в резонанс на частоте, установленной в 1 этапе, изменением образцовой емкости Собр. Полученные значения добротность контура и образцовой емкости в этом случае обозначим через Q 2 и C 2.
По полученным экспериментальным данным (С1,С2, Q1, Q2) на частоте измерения f с помощью формул, приведенных в табл. 8.1., производят вычисления параметров исследуемого двухполюсника (R эфф, X эфф, L эфф,C эфф , Q эфф). По значениям С1 и С2 можно определить характер реактивности двухполюсника. При С1 больше С2 характер реактивности: Хпос - индуктивный; Хпар - емкостной. При С1 меньше С2 характер реактивности: Хпос - емкостной; Хпар - индуктивный.
8.2.3. Действительные и эффективные параметры катушки индуктивности Куметр позволяет определить эффективные значения добротности, индуктивности, емкости и резистивного сопротивления, так как реальную катушку индуктивности (рис. 8.2.а) заменяют эквивалентной схемой (рис. 8.2.б)
Рис. 8.2. а) Реальная схема катушки индуктивности на высоких частотах. б) Эквивалентная схема катушки индуктивности. где: R - резистивное сопротивление, обусловленное потерями в катушке индуктивности; С0 - собственная емкость катушки; L – действительная индуктивность катушки. Действительные значения параметров индуктивности отличаются от эффективных, вследствие наличия у катушки индуктивности собственной емкости. Связь между эффективными и действительными значениями параметров катушки индуктивности могут быть найдены из условия равенства полных сопротивлений Rэфф + jωL эфф = 1 / (jωC0 + (1 / (R + jωL))) (8.4.) Сделав математические преобразования, и пренебрегая некоторыми слагаемыми в виду их малости, и приравняв действительные и мнимые составляющие обеих частей управления, получим: L эфф = L / (1-ω2 C0L) = L / (1-ω2/ ω2pc) (8.5) Rэфф = R / (1-ω2C0L)2= R / (1-ω2/ω2pc)2 (8.6) Отсюда можно определить действительные значения: действительное значение индуктивности L= L эфф /(1+ ω2 C0 L эфф), (8.7) действительное значение резистивного сопротивления R= Rэфф (1- ω 2C0L)2 (8.8) действительное значение добротности Q = Q эфф / (1- ω 2LC0) (8.9) Собственная резонансная частота катушки индуктивности fpc=1/(2π Таблица 8.1
Таблица 8.1(продолжение)
В приведенных формулах размерность величин: f – [кГц]; C1 и C2 - [пФ]; L -[мкГн]; R и X - [Ом].
8.2.4. Измерение действительного значения индуктивности и
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 500; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.140.98 (0.013 с.) |

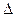 Ах=d*Ах / 100 (8.1.)
Ах=d*Ах / 100 (8.1.)

 )(8.10)
)(8.10)










