
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет простых цепей постоянного токаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Практические занятия Задачи и упражнения
Решение задачи выполняется в три этапа. Сначала нужно сделать расчеты и определить искомые величины. Затем нужно проверить правильность решения (в учебных задачах проверка обязательна). Наконец, нужно оформить решение в соответствии с требованиями преподавателя, кафедры, аттестационной комиссии, заказчика, научного журнала и т.д. Хорошо известно, что в тех случаях, когда учебные задачи решают для тренировки, оформлением решения часто пренебрегают. Вследствие этого искусство оформления и публичного представления своих работ является большой редкостью. Сначала помещены простые задачи, которые, вообще говоря, нужно было научиться решать при изучении физики в школе и вузе. В дальнейшем, задачи и упражнения для самостоятельного решения представлены по темам теоретического раздела учебного пособия. В начале каждой темы дается образец решения и оформления типичной задачи.
Линейные электрические цепи постоянного тока В установившихся режимах
Задача 12. Задана схема электрической цепи (рис. 10.13) и параметры ее элементов
Рис. 10.13 Решение. Объединим точки
Рис. 10.14
Резисторы
Эквивалентная схема цепи показана на рис. 10.15.
Рис. 10.15
Составим и решим систему уравнений Кирхгофа относительно токов
Система уравнений с численными значениями параметров
Искомые токи можно найти, например, методом исключения неизвестных:
Подробности вычислений не представляют интереса. Так как детали решения опущены, необходима проверка полученных результатов, например, путем подстановки значений токов в уравнения (10.1):
Остается найти токи в параллельных резисторах
Напряжение направлено от
(направление тока
(плюс амперметра находится на верхнем зажиме; предполагается, что амперметр имеет двухстороннюю шкалу и может показывать, как положительные, так и отрицательные значения токов).
Задача 13. Задана схема (рис. 10.16) и параметры электрической цепи
Рис. 10.16
Задача 14. Задана схема (рис. 10.17) и параметры электрической цепи
Рис. 10.17 Задача 15. Изменяя сопротивление
Рис. 10.18
Задача 16. Треугольник сопротивлений
Рис. 10.19
Задача 17. Задана схема (рис. 10.20) и параметры электрической цепи
Рис. 10.20
Задача 18. Задана схема электрической цепи (рис.10. 21) и ее параметры
Рис. 10.21
Задача 19. Схема электрической цепи показана на рис. 10.6. Объясните с помощью теоремы об эквивалентном генераторе, как изменится ток в резисторе
Четырехполюсники
Задача 44. Известны параметры элементов (
Рис. 10..46 Решение. В режиме холостого хода, когда
Уравнения четырехполюсника в режиме холостого хода принимают вид
следовательно,
В режиме короткого замыкания, когда
Уравнения четырехполюсника в режиме короткого замыкания принимают вид
следовательно,
Проверка: 1) четырехполюсник симметричен, необходимое условие Характеристическое сопротивление четырехполюсника можно определить по формуле (7.14)
Постоянная передачи согласно формуле (7.16) равна
Передаточную функцию по напряжению в режиме холостого хода можно найти из соотношения (10.9)
Модуль передаточной функции
показывает, что при увеличении частоты входного напряжения (без изменения его действующего значения) от 0 до бесконечности выходное напряжение уменьшается от
показывает, что при увеличении частоты отставание выходного напряжения по фазе возрастает до
Задача 45. Рассматривая трансформатор (рис. 10.47) как четырехполюсник, определите его постоянные
Рис. 10.47
Задача 46. Считая известными постоянные четырехполюсника Дополнительное упражнение. Проверьте полученные формулы на примере четырехполюсника, показанного на рис. 10.46. Кроме выражений для постоянных четырехполюсника, которые приведены в решении задачи 10.44, можно использовать выражения для
Задача 47. Замените четырехполюсник с известными постоянными
Задача 48. Постройте четырехполюсник с постоянными
Несинусоидальными ЭДС
Задача 49. К двухполюснику (рис. 10.48) приложено несинусоидальное напряжение
Известны параметры его элементов
Рис. 10.48 Решение. 1. Расчет постоянных составляющих тока и напряжений. Конденсатор представляет собой разрыв в цепи постоянного тока, постоянная составляющая тока
По второму закону Кирхгофа постоянные составляющие напряжения на конденсаторе и входного напряжения равны:
2. Расчет первых гармоник тока и напряжений. Полное сопротивление цепи первой гармонике тока равно
Действующее значение первой гармоники входного напряжения
Действующее значение первой гармоники тока
Первые гармоники напряжений на элементах цепи (действующие значения)
3. Расчет третьих гармоник тока и напряжений. Полное сопротивление цепи третьей гармонике тока равно
Действующее значение третьей гармоники входного напряжения
Действующее значение третьей гармоники тока
Третьи гармоники напряжений на элементах цепи
4. Расчет показаний приборов. Действующее значение входного напряжения равно геометрической сумме действующих значений его гармонических составляющих (И 8.6)
Действующее значение тока
Действующие значения напряжений на резисторе, катушке и конденсаторе
Высшие гармоники входного напряжения не заданы и не могут быть учтены в расчете. Дополнительное упражнение. Определить активную мощность, потребляемую двухполюсником.
Задача50. К двухполюснику (рис. 10.49) приложено несинусоидальное напряжение
Известны параметры его элементов
Рис. 10.49
Задача 51. Последовательно с источником напряжения
Рис. 10.50
Задача 52. Схема четырехполюсника показана на рис. 10.46, его передаточная функция по напряжению приведена в решении задачи 44. Известны параметры элементов цепи
Проблемные задачи
Задача 53. Закон Ома выражает пропорциональность электрического тока и напряжения на различных двухполюсниках. Коэффициент пропорциональности (электрическое сопротивление) приобретает разный смысл в зависимости от того, какие значения тока и напряжения связывает формула, и в зависимости от того, для каких двухполюсников она применяется. 1. Объясните обозначения в следующих формулах и область применения каждой из них:
2. Объясните, в чем сходство и в чем различие коэффициентов в формулах (1.1) и (3.8). 3. В формулах (3.11) и (3.14) коэффициенты формально играют роль электрического сопротивления. Опишите физический процесс, который характеризуется электрическим сопротивлением, и процессы, которые характеризуются коэффициентами в формулах (3.11) и (3.14). Покажите, что коэффициенты в этих формулах 4. Объясните сходство и различие коэффициентов в формулах (3.8) и (3.22). 5. Какую дополнительную информацию несет формула (4.4) по сравнению с формулой (3.8)? Ответьте на аналогичный вопрос, сравнивая формулы (3.12) и (4.4), затем формулы (3.15) и (4.6), наконец, формулы (3.22) и (И 4.15). 6. Какую роль играет закон Ома при записи системы уравнений Кирхгофа? 7. В элементарной физике формулу
часто называют обобщенным законом Ома (здесь 8. Какую роль играют соглашения о направлениях тока и напряжения на двухполюсниках при записи различных вариантов закона Ома?
Задача 54. Запишите формулировку первого закона Кирхгофа в трех вариантах: 1) для цепей постоянного тока, 2) цепей переменного тока, 3) цепей переменного синусоидального тока в комплексной форме. Подчеркните слова, которыми отличаются первая и вторая формулировки, затем слова, которыми отличаются первая и третья формулировки. Объясните принципиальные различия между тремя формулировками, укажите область применения каждой из них. Дополните каждую из формулировок правилом знаков. Почему правило знаков формулируется одинаковым образом для постоянных и переменных токов? Какой смысл имеет термин «направление тока» по отношению к комплексному току?
Задача 55. Сформулируйте второй закон Кирхгофа в трех вариантах: 1) для напряжений в цепи постоянного тока, 2) мгновенных напряжений в цепи переменного, 3) комплексных напряжений в цепи переменного синусоидального тока (не используя понятия ЭДС). Объясните принципиальные отличия первой формулировки от второй и первой формулировки от третьей. Укажите область применения каждой из формулировок. Дайте эквивалентную формулировку второго закона Кирхгофа (с использованием понятия ЭДС) в тех же трех вариантах, что и раньше. На каком основании часть напряжений в уравнениях, составленных по второму закону Кирхгофа, заменяется электродвижущими силами? Дополните каждую из формулировок второго закона Кирхгофа правилом знаков. В каком смысле говорят о направлении электрического напряжения (ведь напряжения - это скалярная величина, оно даже не связано с направлением движения зарядов, как электрический ток)? Почему правило знаков формулируется одинаковым образом для постоянных и переменных напряжений? При каком условии понятия направления напряжения и полярности напряжения (точнее, предполагаемой полярности напряжения) эквивалентны?
Задача 56. Сформулируйте основную задачу теории электрических цепей. Опишите алгоритм решения этой задачи с помощью законов Кирхгофа. Сколько уравнений в системе уравнений Кирхгофа составляется по первому и сколько по второму закону Кирхгофа? Какую роль играет закон Ома при выводе системы уравнений Кирхгофа для конкретной цепи? К какому классу математических задач относится решение системы уравнений Кирхгофа для цепей постоянного тока и цепей переменного синусоидального тока в комплексной форме? Почему решение системы уравнений Кирхгофа относительно постоянных токов в первом случае и относительно комплексных токов во втором случае относится к одному и тому же классу математических задач? На каком основании утверждают, что расчет цепи переменного синусоидального тока символическим (комплексным) методом аналогичен расчету цепи постоянного тока? К какому классу математических задач относится решение системы уравнений Кирхгофа для цепей переменного тока? Почему при выводе системы уравнений Кирхгофа для цепи переменного тока недостаточно закона Ома? Какие еще соотношения (законы) приходится привлекать в этом случае для вывода системы уравнений Кирхгофа? Как учитывается в системе уравнений Кирхгофа явление взаимной индукции?
Задача 57. Известна схема электрической цепи постоянного тока и параметры ее элементов за исключением одной ЭДС, зато известен ток в одной из ветвей цепи. Требуется определить ЭДС. Докажите, что эта задача разрешима. Сформулируйте алгоритм ее решения. Рассмотрите другой вариант предыдущей задачи, когда известен один из токов в цепи, но неизвестно сопротивление одного резистора. Требуется определить это сопротивление. Сформулируйте алгоритм решения задачи.
Задача 58. Сформулируйте баланс мощностей для цепей постоянного тока и баланс комплексных мощностей для цепей переменного синусоидального тока (не содержащих катушек взаимной индуктивности). Отметьте принципиальное сходство обеих формулировок и их различие в деталях. Запишите уравнения баланса, выразив мощности через токи и напряжения. Можно ли утверждать, что баланс комплексных мощностей равносилен двум равенствам: балансу активных мощностей и балансу реактивных мощностей? Какие доводы вы можете привести в подтверждение своего мнения? Объясните, почему мощность источника (активная мощность в цепях переменного тока) является алгебраической величиной, при каких условиях она принимает положительные значения, а при каких условиях отрицательные. Какие процессы в цепях переменного тока характеризует реактивная мощность?
Задача 59. Расчет цепей переменного синусоидального тока символическим методом по форме аналогичен расчету цепей постоянного тока. В обоих случаях основные уравнения отличаются только обозначениями. Оба расчета отличаются лишь деталями вычислений. 1. Сравните алгоритм расчета постоянных токов с помощью системы уравнений Кирхгофа и алгоритм расчета комплексных токов аналогичным методом. Перечислите одинаковые этапы обоих алгоритмов, отметьте отличительные особенности каждого из них. В чем заключаются трудности решения комплексных уравнений по сравнению с решением уравнений с действительными переменными? 2. Запишите алгоритм расчета постоянных токов методом наложения. Сформулируйте аналогичный алгоритм для расчета комплексных токов, выделяя его особенности по сравнению с первым алгоритмом. 3. Сформулируйте теорему об эквивалентном генераторе для цепей постоянного тока, а затем аналогичную теорему для цепей переменного синусоидального тока в комплексной форме. 4. Сформулируйте условия эквивалентности двухполюсников в цепях постоянного тока, а затем аналогичные условия для цепей переменного синусоидального тока в комплексной форме. 5. Объясните, почему уравнения Кирхгофа, составленные для цепи переменного синусоидального тока в комплексной форме, после перехода к пределу при
Задача 60. Известна схема электрической цепи постоянного тока и параметры ее элементов за исключением одной ЭДС. Число неизвестных величин на единицу больше числа неизвестных токов. Можно ли добавить к системе уравнений Кирхгофа уравнение баланса мощностей и получить таким образом систему уравнений, позволяющую определить все искомые величины (все токи и неизвестную ЭДС)? Какие соображения вы можете привести в качестве обоснования своей точки зрения?
Задача 61. В цепи, схема которой показана на рис. 11.1, известны показания приборов. Требуется определить параметры катушек
Рис. 11.1 Разрешима ли эта задача в случае, когда в цепи нет ваттметра? Докажите свое мнение.
Задача 62. Схема цепи показана на рис. 11.2. Известны показания приборов (ток и напряжения на катушках и напряжение источника). Требуется определить параметры катушек. Разрешима ли эта задача? Ответ нужно обосновать.
Задача 63. В цепи переменного синусоидального тока (рис. 11.3) параметры
Рис. 11.2
ком соотношении между параметрами
Рис. 11.3 Указание:
Задача 64. Определите входное комплексное сопротивление двухполюсника, схема которого показана на рис. 11.4.
Рис. 11.4 Указание: сделайте развязку магнитной связи между катушками.
Задача 65. Запишите уравнения трансформатора (схема на рис. 5.12). Затем измените разметку однополярных зажимов, переместив метку с верхнего зажима вторичной катушки на ее нижний зажим. В дальнейшем нужно будет учесть все последствия этого решения. Сначала внесите изменения в уравнения трансформатора. Затем покажите, что несмотря на эти изменения в записи уравнений их решение (то есть токи Практические занятия Задачи и упражнения
Решение задачи выполняется в три этапа. Сначала нужно сделать расчеты и определить искомые величины. Затем нужно проверить правильность решения (в учебных задачах проверка обязательна). Наконец, нужно оформить решение в соответствии с требованиями преподавателя, кафедры, аттестационной комиссии, заказчика, научного журнала и т.д. Хорошо известно, что в тех случаях, когда учебные задачи решают для тренировки, оформлением решения часто пренебрегают. Вследствие этого искусство оформления и публичного представления своих работ является большой редкостью. Сначала помещены простые задачи, которые, вообще говоря, нужно было научиться решать при изучении физики в школе и вузе. В дальнейшем, задачи и упражнения для самостоятельного решения представлены по темам теоретического раздела учебного пособия. В начале каждой темы дается образец решения и оформления типичной задачи.
Расчет простых цепей постоянного тока
Задача 1. Задана схема (рис. 10.1) и параметры электрической цепи
Рис. 10.1
Решение. Резисторы
Эквивалентная схема электрической цепи показана на рис. 10.2.
Рис. 10.2
Резисторы
Ток источника по закону Ома равен
Напряжение между точками
Токи параллельных ветвей (рис. 10.1)
Проверка правильности решения с помощью баланса мощностей является самой надежной в теории электрических цепей. Она позволяет не только убедиться в правильности вычислений, но и в правильности использованных уравнений. Мощности, потребляемые резисторами по отдельности, равны
Мощность, потребляемая всеми резисторами цепи,
Мощность источника
Мощность источника равна мощности приемников электрической энергии
В дальнейшем решение этой задачи многократно встречается в качестве фрагмента решений более сложных задач. Задача 2. Задана схема электрической цепи (рис. 10.3) и параметры ее элементов
Рис.10.3
Задача 3. Задана схема электрической цепи (рис. 10.4) и параметры ее элементов
Рис.10.4 Задача 4. Задана схема электрической цепи (рис. 10.5) и сопротивления резисторов
Рис.10.5
Задача 5. В электрической цепи, схема которой показана на рис. 10.6, происходит увеличение сопротивления
Рис.10.6
Основные понятия и законы теории электрических цепей
Задача 6. Через идеальную катушку проходят однополярные импульсы тока треугольной формы (рис. 10.7). Определить напряжение на катушке, построить его принципиальный график.
Рис.10.7
Решение. Напряжение на
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 505; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.70.169 (0.015 с.) |

 = 30 В,
= 30 В,  = 20 В,
= 20 В,  = 10 Ом,
= 10 Ом,  = 20 Ом. Определите токи во всех ветвях цепи, включая показание амперметра (принять
= 20 Ом. Определите токи во всех ветвях цепи, включая показание амперметра (принять  ).
).
 и
и  , соединенные проводом с нулевым сопротивлением. Схема преобразованной цепи показана на рис. 10.14. Резистор
, соединенные проводом с нулевым сопротивлением. Схема преобразованной цепи показана на рис. 10.14. Резистор  по-прежнему присоединен к точкам
по-прежнему присоединен к точкам  .
.
 и
и  Ом.
Ом.
 ,
,  и
и  . В цепи (рис. 10.15) два узла, для одного из них (
. В цепи (рис. 10.15) два узла, для одного из них ( ) составим уравнение по первому закону Кирхгофа. Еще два уравнения составим по второму закону Кирхгофа для контуров I и II.
) составим уравнение по первому закону Кирхгофа. Еще два уравнения составим по второму закону Кирхгофа для контуров I и II. ,
, ,
, .
. , (10.1)
, (10.1) .
. А,
А,  А,
А,  А.
А. ,
, ,
, .
. и
и  и показание амперметра. Напряжение между точкой
и показание амперметра. Напряжение между точкой  на рис. 10.15 равно
на рис. 10.15 равно В.
В. А,
А, А
А противоположно направлению напряжения
противоположно направлению напряжения  , нарушено соглашение И 1.25.). Показание амперметра найдем по первому закону Кирхгофа для узла
, нарушено соглашение И 1.25.). Показание амперметра найдем по первому закону Кирхгофа для узла  А.
А. 60 В,
60 В, 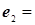 12 В,
12 В,  Ом,
Ом,  Ом. Определить показание вольтметра, считая прибор идеальным (
Ом. Определить показание вольтметра, считая прибор идеальным (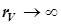 ).
).
 12 В,
12 В,  4 Ом,
4 Ом,  6 Ом. Определить показание амперметра, считая прибор идеальным (
6 Ом. Определить показание амперметра, считая прибор идеальным ( ).
).
 , можно установить нулевой ток в ветви с амперметром (рис. 10.18). Определите, при каком сопротивлении
, можно установить нулевой ток в ветви с амперметром (рис. 10.18). Определите, при каком сопротивлении  ,
, 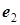 и
и  . Может ли повлиять на результат сопротивление амперметра?
. Может ли повлиять на результат сопротивление амперметра?
 2 Ом подключен к электрической цепи, которая питает его токами
2 Ом подключен к электрической цепи, которая питает его токами  ,
,  и
и  (рис. 10.19). Определите токи в резисторах при
(рис. 10.19). Определите токи в резисторах при  А. Объясните, почему ток
А. Объясните, почему ток 
 1 А,
1 А,  А. Вновь проверьте полученный результат с помощью уравнений Кирхгофа.
А. Вновь проверьте полученный результат с помощью уравнений Кирхгофа.
 20 Ом,
20 Ом,  40 Ом. Определить ток
40 Ом. Определить ток  методом эквивалентного генератора.
методом эквивалентного генератора.
 при уменьшении его сопротивления. Как изменится напряжение на этом резисторе? Как изменятся токи в остальных ветвях цепи?
при уменьшении его сопротивления. Как изменится напряжение на этом резисторе? Как изменятся токи в остальных ветвях цепи? и
и  ), из которых собран четырехполюсник (рис. 10.46). Определить постоянные четырехполюсника, его характеристическое сопротивление и постоянную передачи, передаточную функцию по напряжению в режиме холостого хода.
), из которых собран четырехполюсник (рис. 10.46). Определить постоянные четырехполюсника, его характеристическое сопротивление и постоянную передачи, передаточную функцию по напряжению в режиме холостого хода.
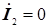 ,
, , (10.9)
, (10.9) . (10.10)
. (10.10) ,
, 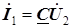 ,
, ,
, .
. ,
, ,
, . (10.11)
. (10.11) ,
,  ,
, ,
, .
. выполняется; 2) условие взаимности
выполняется; 2) условие взаимности  также выполняется.
также выполняется. .
. .
. .
.
 до нуля. Аргумент передаточной функции
до нуля. Аргумент передаточной функции
 .
. и
и  .
.
 и в режиме короткого замыкания
и в режиме короткого замыкания  .
. , подключенной к его входным зажимам, эквивалентным генератором. Определите параметры эквивалентного генератора.
, подключенной к его входным зажимам, эквивалентным генератором. Определите параметры эквивалентного генератора. ,
,  .
. В.
В. 6 Ом,
6 Ом,  1 Ом,
1 Ом,  9 Ом. Определить показания амперметра и вольтметров электромагнитной системы.
9 Ом. Определить показания амперметра и вольтметров электромагнитной системы.
 . Соответствующие составляющие напряжения на конденсаторе и входного напряжения равны:
. Соответствующие составляющие напряжения на конденсаторе и входного напряжения равны: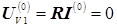 ,
,  .
. В.
В.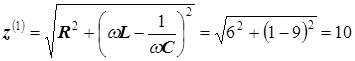 Ом.
Ом. В.
В. А.
А. В,
В, В,
В, В.
В. Ом.
Ом. В.
В. А.
А. В,
В, В,
В, В.
В. В.
В. А.
А. В,
В, В,
В, В.
В.
 В и резистором
В и резистором  , когда
, когда  и
и  , и
, и  , когда
, когда  или
или  . Построить график мгновенного тока
. Построить график мгновенного тока  , записать его аналитическое выражение при условии, что управляющее напряжение
, записать его аналитическое выражение при условии, что управляющее напряжение  В. Определить среднее (за период) и действующее значения тока.
В. Определить среднее (за период) и действующее значения тока.
 1 мкФ. График входного напряжения показан на рис. 8.2, его разложение на гармоники представлено формулой (8.1),
1 мкФ. График входного напряжения показан на рис. 8.2, его разложение на гармоники представлено формулой (8.1),  В,
В,  . Определите амплитуды и начальные фазы гармоник входного и выходного напряжений (до седьмой включительно).
. Определите амплитуды и начальные фазы гармоник входного и выходного напряжений (до седьмой включительно). (1.1);
(1.1);  (И 2.21);
(И 2.21);  (3.8);
(3.8); (3.11 и 3.12);
(3.11 и 3.12);  (3.14 и 3.15);
(3.14 и 3.15); (3.22);
(3.22);  (4.4);
(4.4);  (4.5);
(4.5); (4.6);
(4.6);  (И 4.15).
(И 4.15). и
и  имеют размерность электрического сопротивления.
имеют размерность электрического сопротивления. (11.1)
(11.1) - ЭДС источника,
- ЭДС источника,  - его внутреннее сопротивление,
- его внутреннее сопротивление,  - сопротивление приемника (нагрузки)). Какие основания имеются для такого обобщения? Аналогом какого выражения из приведенных выше является формула (11.1)? Какое название было бы для формулы (11.1) более точным, чем «обобщенный закон Ома»?
- сопротивление приемника (нагрузки)). Какие основания имеются для такого обобщения? Аналогом какого выражения из приведенных выше является формула (11.1)? Какое название было бы для формулы (11.1) более точным, чем «обобщенный закон Ома»? (
( - круговая частота напряжения или тока источника) превращаются в уравнения Кирхгофа для той же цепи с источником постоянного напряжения (или тока). Проверьте правильность этого утверждения на цепях, схемы которых показаны на рис. 10.29, 10.31 и 10.41.
- круговая частота напряжения или тока источника) превращаются в уравнения Кирхгофа для той же цепи с источником постоянного напряжения (или тока). Проверьте правильность этого утверждения на цепях, схемы которых показаны на рис. 10.29, 10.31 и 10.41. ,
,  и
и  ,
,  . Правильно ли поставлена задача, существует ли ее решение? Докажите правильность своего ответа.
. Правильно ли поставлена задача, существует ли ее решение? Докажите правильность своего ответа.
 и
и 

 .
.
 и
и  ) остались неизменными.
) остались неизменными. 12 В,
12 В, 
 с сопротивлением
с сопротивлением Ом.
Ом.
 Ом.
Ом. А.
А. В.
В. А,
А, А.
А. Вт,
Вт, Вт,
Вт, Вт.
Вт. Вт.
Вт. Вт.
Вт. Вт.
Вт. Ом,
Ом,  20 Ом. Определить показания измерительных приборов. Приборы можно считать идеальными (сопротивления амперметров равны нулю, сопротивление вольтметра бесконечно велико).
20 Ом. Определить показания измерительных приборов. Приборы можно считать идеальными (сопротивления амперметров равны нулю, сопротивление вольтметра бесконечно велико).
 Ом,
Ом,  60 Ом. Определить показание амперметра (считая его сопротивление равным нулю).
60 Ом. Определить показание амперметра (считая его сопротивление равным нулю).
 50 В,
50 В,  80 Ом,
80 Ом,  20 Ом,
20 Ом,  30 Ом. Известно показание амперметра,
30 Ом. Известно показание амперметра,  0,15 А. Определить ЭДС источника.
0,15 А. Определить ЭДС источника.
 . Объясните, как изменятся токи в этой цепи (анализируя уравнения и не прибегая к вычислениям).
. Объясните, как изменятся токи в этой цепи (анализируя уравнения и не прибегая к вычислениям).





