
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет и определение параметров пассивных четырехполюсников.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Дан Т или П – образный симметричный четырехполюсник, схема которого представлена на рис.3 (а,б), а величины полных сопротивлений Требуется: 1. Определить параметры элементов цепи ( 2. Определить сопротивление холостого хода 3. По найденным сопротивлениям найти коэффициенты четырехполюсника в форме А (т.е. коэффициенты А,В,С,D или 4. Определить напряжение 5. Определить характеристическое сопротивление
а) б) Рис.3 – Т (а) и П (б) – образный симметричный четырехполюсник
Таблица 3 – Исходные данные для расчета
Продолжение таблицы 3
Методические указания и пример выполнения задачи № 1 Приведем пример расчета сложной цепи постоянного тока. Дано: задана электрическая цепь (рис.1.1), заданы величины сопротивлений
Рис.1.1 Рис.1.2 Решение: 1. Составим расчетную схему цепи. Для этого заменим источник тока
2. Запишем систему уравнений необходимых для определения токов ветвей по законам Кирхгофа. Для этого: 2.1 Выберем произвольно направления токов в ветвях схемы и направление обхода контуров по часовой стрелке (рис.1.3). 2.2 Определим число уравнений, которые необходимо составить по первому и второму законам Кирхгофа. Общее число уравнений должно соответствовать числу неизвестных токов, в нашем случае - шести. Число уравнений, составляемых по первому закону Кирхгофа, определяем по формуле 2.3 Составляем систему из трех уравнений по первому закону Кирхгофа (для узлов 1, 2 и 3) и из трех уравнений по второму закону Кирхгофа (контуры I, II и III). Система имеет вид:
Рис.1.3 3. Для определения токов ветвей воспользуемся методом контурных токов (МКТ). Метод контурных токов выводится из метода непосредственного применения законов Кирхгофа путем исключения уравнений, составляемых по первому закону Кирхгофа. Введение обобщенных переменных - контурных токов позволяет значительно сократить общее число решаемых уравнений. Полученные уравнения решаются относительно контурных токов. Затем токи в ветвях выражаются через найденные контурные токи. 3.1 Так как число уравнений, составляемых по второму закону Кирхгофа равно трем, то и число неизвестных контурных токов в нашем случае - три. Обозначим контурные токи: 3.2 Выберем направление контурных токов совпадающим с направлением вращения часовой стрелки. Номера контуров совпадают с индексами контурных токов. 3.3 Составим систему из трех уравнений по второму закону Кирхгофа относительно контурных токов. При этом учтем падение напряжения на резистивных элементах от каждого контурного тока, текущего по нему. На резистор Первое уравнение соответствует первому контуру, второе - второму и т.д.:
Рис.1.4 Подставим в полученные уравнения величины заданных сопротивлений, ЭДС и получим: Если в результате решения системы уравнений какой-либо контурный ток окажется отрицательным, то это означает, что в действительности направление контурного тока обратно принятому за положительное. Решим систему уравнений, используя (например) программу Excel и получим значения контурных токов:
3.4 Используя выбранные в п.2.1 направления токов ветвей выразим их через найденные контурные токи:
Отметим, что при определении токов 4. Правильность расчета проверим по балансу мощностей. Баланс мощностей вытекает из закона сохранения энергии и сводится к следующему: в любой электрической цепи сумма мощностей отдаваемой источниками энергии равна сумме мощностей потребляемой нагрузками (пассивными элементами электрической цепи). Для цепей постоянного тока баланс мощностей может быть записан в виде:
где Мощность источников определим по формуле, составленной согласно схемы рис. 1.4:
Мощность потребителей (нагрузок) найдем по формуле:
После подстановки значений получим:
Баланс мощности сошелся, следовательно, расчет выполнен верно.
5. Построим потенциальную диаграмму для контура abcdea цепи (рис.1.5). Потенциальная диаграмма представляет собой график изменения потенциала при обходе цепи, построенный в прямоугольной системе координат, в которой по оси абсцисс откладываются в определенном масштабе сопротивления участков цепи, а по оси ординат – потенциалы соответствующих точек. Примем потенциал точки а равным нулю ( С учетом сказанного запишем:
Изобразим потенциальную диаграмму. По оси абсцисс отложим сумму сопротивлений контура (
Рис. 1.5 Рис.1.6
Нанесенные точки соединим прямыми, на идеальных источниках ЭДС наблюдаются скачки потенциалов на величину ЭДС: Потенциальная диаграмма может быть получена и опытным путем. Для этого достаточно один зажим вольтметра подключить к точке a электрической цепи, а другой зажим подключать поочередно к другим точкам контура, что позволит по показаниям вольтметра определить потенциалы соответствующих точек контура. 6. Для преобразования схемы в двухконтурную необходимо найти сопротивления, включенные по схеме «звезда» или «треугольник» и эквивалентно преобразовать одно в другое. На рис.1.7 показаны такие соединения и формулы эквивалентного перехода. «Треугольник»
Для получения двухконтурной схемы в вышеизложенной задаче произведем замену треугольника сопротивлений
В результате преобразований получим схему, изображенную на рис.1.8. Упростим полученную цепь, заменив последовательно соединенные элементы эквивалентными (рис.1.9).
Рис. 1.8 Рис. 1.9
7. Используя полученную схему (рис.1.9), выберем на ней произвольно направления токов и проведем их расчет используя один из заданных методов расчета: метод двух узлов (МДУ) или метод наложения (МН). 7.1 Метод двух узлов является частным случаем метода узловых потенциалов. МДУ применяется в тех случаях, когда несколько источников и приемников электрической энергии включены параллельно, при этом в схеме имеются только два узла. Найдем напряжение между узлами а и b по формуле
где знак плюс в числителе берем, если стрелка ЭДС направлена к узлу а, в противном случае берем знак минус; Для рассматриваемого примера:
где
Используя обобщенный закон Ома, найдем токи в ветвях:
Найденное решение проверим по балансу мощностей: мощность источников
мощность нагрузок
Результат совпадает с полученным ранее в п.4. Это указывает на правильность проведения эквивалентных преобразований в цепи. 7.2 Суть метода наложения заключается в том, что в линейной электрической цепи, находят так называемые частичные токи, которые создаются каждым источником ЭДС схемы в отдельности. Реальный ток в ветви представляет собой алгебраическую сумму частичных токов, текущих по этой ветви. Частичные токи находят любым из известных методов расчета, например, по закону Ома.
Рис.1.10 Рис.1.11 Составимрасчетную схему для определения частичных токов от первой ЭДС (рис.1.10). Расчет цепи проведем по закону Ома:
напряжение между узлами
Оставим в исходной электрической цепи (рис. 1.9) только ЭДС
Тогда токи параллельных ветвей равны:
Токи в ветвях (рис.1.9) определим как алгебраическую сумму соответствующих частичных токов (рис.1.10; рис.1.11).
Найденное решение проверим по балансу мощностей: Мощность источников
Мощность нагрузок
Результат совпадает с полученным ранее в п.4. Это указывает на правильность проведенных расчетов.
Методические указания и пример выполнения задачи № 2 Принцип расчета сложной цепи переменного тока рассмотрим на примере, приведенном ниже: Дано:
Решение: 1. Составим расчетную схему цепи, согласно варианта задания (рис.2.1)
Рис.2.1 Рис.2.2
2. Определяем реактивные сопротивления элементов цепи:
где 3. Найдем полные комплексные сопротивления ветвей электрической цепи:
4. Изобразим схему замещения (рис. 2.2). 5. Определим число уравнений, составляемых по первому закону Кирхгофа по формуле
В полученные уравнения подставим числовые значения сопротивлений
Решим систему, используя программу Excel, и получим значения токов ветвей. 6. Найденные значения токов запишем в алгебраической и показательной формах:
Запишем мгновенные значения токов ветвей в виде
7. Сделаем проверку расчётов по балансу мощностей. Согласно схемы рис. 2.2, запишем:
здесь
где Баланс мощности сошелся, т.е. 8. Определим токи ветвей, используя метод контурных токов. Выберем направление контурных токов по часовой стрелке, рис.2.3.
Рис. 2.3 Рис.2.4
Тогда система из двух уравнений примет вид:
Сделаем подстановку численных значений и получим:
Решим систему и определим значения контурных токов:
Выразим токи ветвей через контурные токи:
9. Сравним результаты расчетов по п.5 и п.8. 10. Построим векторную диаграмму токов и топографическую диаграмму напряжений, рассчитанную для внешнего контура цепи (рис.2.4). Векторная диаграмма токов - это реализация первого закона Кирхгофа на комплексной плоскости. Топографическая диаграмма - это картина распределения комплексных потенциалов точек электрической цепи на комплексной плоскости. Определим потенциалы точек внешнего контура цепи. Примем потенциал точки а равным нулю и, относительно него, определим потенциалы остальных точек:
Обычно топографическую диаграмму рисуют совмещенной с векторной диаграммой токов (рис.2.5), масштаб по току
Рис. 2.5
Правильность построения топографической диаграммы легко проверяется путем сопоставления векторов падения напряжения на элементах цепи с соответствующими векторами токов. Действительно, напряжение на резистивном элементе 11. Метод эквивалентного генератора применяется для расчета электрических цепей, в которых требуется найти ток в какой - либо одной ветви. Выделим нагрузку, в которой требуется найти ток, а оставшуюся электрическую цепь примем за активный двухполюсник (или за эквивалентный генератор), затем расчетным путем определим параметры схемы замещения активного двухполюсника (эквивалентного генератора) - Рассчитаем ток второй ветви
Рис. 2.6 Рис. 2.7
Для определения
Для определения ЭДС эквивалентного генератора рассмотрим активный двухполюсник. Для этого из исходной схемы убираем нагрузку Это напряжение можно определить с помощью расчета тока I:
Зная ток
отсюда
Рис. 2.8 Рис.2.9
По эквивалентной схеме генератора с подключенной к нему нагрузкой
Результат расчета сошелся с полученным ранее, следовательно, вычисления выполнены верно.
Методические указания и пример выполнения задачи № 3
Принцип расчета симметричного Т-образного четырехполюсника рассмотрим на примере, приведенном ниже:
Дано: Т-образный четырехполюсник (рис.3а). Решение: 1. Определим параметры элементов цепи ( Схема замещения каждого из сопротивлений составляется относительно заданной алгебраической формы записи числа. Так как
то, для чисто активной нагрузки ( для активно-индуктивной ( для активно-емкостной (
Рис.3.1
При заданном значении частоты
2. Определим сопротивления холостого хода Сопротивления четырехполюсника
Так как четырехполюсник симметричный, то 3. По найденным сопротивлениям определим коэффициенты четырехполюсника в форме А (т.е. коэффициенты А,В,С,D или
Связь между входными и выходными напряжениями и токами в четырехполюснике описывается уравнениями формы А:
Коэффициенты
Для симметричного четырехполюсника, Для определения коэффициентов
Используя известное выражение определим сначала параметр параметры
Сделаем проверку правильности расчетов используя уравнение связи:
4. Определим напряжение Изобразим расчетную схему цепи (рис.3.2):
Рис.3.2 Определяем полные сопротивления ветвей:
Для расчета цепи используем метод эквивалентных преобразований. Определим эквивалентное сопротивление цепи относительно зажимов
Используя закон Ома определим ток
Для определения тока
Определим напряжение
Потребляемая мощность
Мощность на нагрузке
КПД четырехполюсника -
5. Определим характеристическое сопротивление
Характеристическое сопротивление симметричного четырехполюсника это такое сопротивление нагрузки ( Величина характеристического сопротивления определяется как среднее геометрическое входных сопротивлений при холостом ходе и коротком замыкании на выходе симметричного четырехполюсника:
Примем
В результате расчета получили: при нагрузке симметричного четырехполюсника на характеристическое сопротивление, его входное сопротивление повторяет сопротивление загрузки При рассмотрении четырехполюсника следует знать не только схему, параметры сопротивлений, форму и коэффициенты четырехполюсника, а еще такую характеристику, как функцию передачи, что определяет затухание сигнала и изменение сдвига фаз в четырехполюснике. Для симметричного четырехполюсника, нагруженного на
комплексное число
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 722; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.015 с.) |

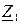 и
и  при частоте 50 Гц указаны в таблице 3.
при частоте 50 Гц указаны в таблице 3.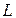 и
и  ) и изобразить заданную электрическую схему, включая вместо
) и изобразить заданную электрическую схему, включая вместо  ,
,  и короткого замыкания
и короткого замыкания  четырехполюсника.
четырехполюсника. ) и проверить соотношение между ними (
) и проверить соотношение между ними ( ).
). , токи
, токи  и
и  , мощности
, мощности  и
и  и КПД
и КПД  четырехполюсника при значениях напряжения
четырехполюсника при значениях напряжения  и активном сопротивлении нагрузки
и активном сопротивлении нагрузки 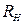 (подключено к клеммам
(подключено к клеммам  ), указанных в таблице 3.1.
), указанных в таблице 3.1. четырехполюсника и проверить его расчетом, приняв сопротивление нагрузки
четырехполюсника и проверить его расчетом, приняв сопротивление нагрузки  , а также определить постоянную передачи четырехполюсника.
, а также определить постоянную передачи четырехполюсника.

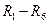 , Э.Д.С.
, Э.Д.С.  и ток источника
и ток источника  :
:  ;
;  ;
;  ;
; 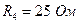 ;
;  ;
;  ;
;  ;
;  .
.

 и изобразим полученную схему цепи (рис.1.2):
и изобразим полученную схему цепи (рис.1.2):
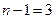 и по второму закону Кирхгофа по формуле
и по второму закону Кирхгофа по формуле  , где
, где  - число узлов,
- число узлов,  - число ветвей рассчитываемой цепи (рис 1.3).
- число ветвей рассчитываемой цепи (рис 1.3).


 . (рис.1.4)
. (рис.1.4) действуют по одному контурному току, а на резисторы
действуют по одному контурному току, а на резисторы  оказывают действие по два контурных тока.
оказывают действие по два контурных тока.




 и
и  учитывалось, что контурный ток, совпадающий по направлению с током ветви, берется со знаком " + ", не совпадающий - со знаком " - ". При этом значения контурных токов подставляются в формулы со своим знаком.
учитывалось, что контурный ток, совпадающий по направлению с током ветви, берется со знаком " + ", не совпадающий - со знаком " - ". При этом значения контурных токов подставляются в формулы со своим знаком. ,
,  - мощность источников; знак плюс у произведения ЭДС на ток берется, если направления стрелок
- мощность источников; знак плюс у произведения ЭДС на ток берется, если направления стрелок  и
и  совпадают, в противном случае берется знак минус,
совпадают, в противном случае берется знак минус, 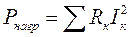 - мощность нагрузок.
- мощность нагрузок.


 ) и найдем (выразим) потенциалы остальных точек относительно потенциала точки а. При этом учтем (по направлению токов на схеме), что ток течет от большего потенциала к меньшему, а стрелка ЭДС направлена в сторону увеличения потенциала.
) и найдем (выразим) потенциалы остальных точек относительно потенциала точки а. При этом учтем (по направлению токов на схеме), что ток течет от большего потенциала к меньшему, а стрелка ЭДС направлена в сторону увеличения потенциала.
 ), по оси ординат нанесем соответствующие потенциалы точек (в общем случае потенциалы точек могут быть положительными и отрицательными числами) контура аbсdea, рис.1.6. При этом учтем, что у идеальных источников ЭДС внутреннее сопротивление равно нулю.
), по оси ординат нанесем соответствующие потенциалы точек (в общем случае потенциалы точек могут быть положительными и отрицательными числами) контура аbсdea, рис.1.6. При этом учтем, что у идеальных источников ЭДС внутреннее сопротивление равно нулю.

 ;
; 
 «Звезда»
«Звезда»



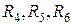 в эквивалентную звезду
в эквивалентную звезду  . Вычисления произведем по формулам:
. Вычисления произведем по формулам: ;
; ;
; .
.


 ,
, - проводимость к -ой ветви.
- проводимость к -ой ветви. ,
,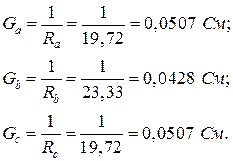


 Баланс мощности сошелся, следовательно, расчет выполнен верно
Баланс мощности сошелся, следовательно, расчет выполнен верно .
.

 А, где
А, где Ом,
Ом, В, тогда токи параллельных ветвей равны:
В, тогда токи параллельных ветвей равны: А,
А,  А.
А. А, где
А, где Ом,
Ом, В.
В. А,
А,  А.
А. А,
А, А,
А,  А.
А.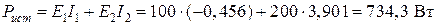
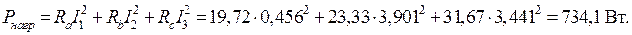 Баланс мощности сошелся, следовательно, расчет выполнен верно.
Баланс мощности сошелся, следовательно, расчет выполнен верно. ;
;  ;
;  ;
;  ;
;  ;
;  ;
; 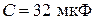 .
.


 .
.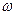 - угловая частота равная:
- угловая частота равная: 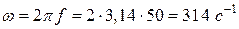 .
. Ом,
Ом, Ом,
Ом, Ом.
Ом. и по второму закону Кирхгофа по формуле
и по второму закону Кирхгофа по формуле  , где
, где  - число узлов,
- число узлов,  - число ветвей. Направления обхода контуров показаны на рис.2.2.
- число ветвей. Направления обхода контуров показаны на рис.2.2.
 , ЭДС
, ЭДС  и получим систему:
и получим систему:

 , где
, где  - действующее значение тока:
- действующее значение тока: ;
; ;
; .
.
 - полная мощность источников цепи,
- полная мощность источников цепи,  - сопряженное значение тока,
- сопряженное значение тока,  -активная мощность источников,
-активная мощность источников,  - реактивная мощность источников.
- реактивная мощность источников.
 - полная мощность нагрузки цепи,
- полная мощность нагрузки цепи,  - активная мощность нагрузки,
- активная мощность нагрузки, 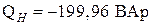 - реактивная мощность нагрузки.
- реактивная мощность нагрузки. и
и  , погрешность связана с неточностью вычислений.
, погрешность связана с неточностью вычислений.



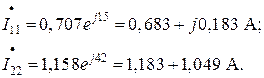

 тогда
тогда
 0,5 А/см, масштаб по напряжению
0,5 А/см, масштаб по напряжению  20 В/см.
20 В/см.
 совпадает по направлению с током
совпадает по направлению с током  ; напряжение
; напряжение 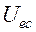 на емкостном элементе отстает от вектора тока
на емкостном элементе отстает от вектора тока  по фазе на
по фазе на  .
. -ЭДС эквивалентного генератора и
-ЭДС эквивалентного генератора и  - сопротивление эквивалентного генератора.
- сопротивление эквивалентного генератора. (рис. 2.6). Согласно данного метода
(рис. 2.6). Согласно данного метода 
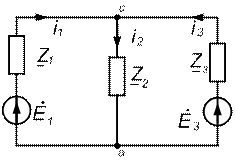

 (элемент, ток которого мы ищем) и все источники. Поскольку идеальные источники ЭДС имеют внутреннее сопротивление равное нулю, то расчетная схема примет вид, показанный на рис. 2.7. Относительно узлов а и с определим эквивалентное сопротивление цепи:
(элемент, ток которого мы ищем) и все источники. Поскольку идеальные источники ЭДС имеют внутреннее сопротивление равное нулю, то расчетная схема примет вид, показанный на рис. 2.7. Относительно узлов а и с определим эквивалентное сопротивление цепи: Ом.
Ом. (рис.2.8).
(рис.2.8).
 , определяем напряжение
, определяем напряжение  . Пусть
. Пусть  , тогда
, тогда
 В.
В.

 А.
А. ;
;  ;
;  ;
;  ;.
;.
 )
) 
 )
) 
 )
) 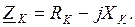

 , параметры катушки и конденсатора будут иметь значения:
, параметры катушки и конденсатора будут иметь значения:
 определим со стороны входных (
определим со стороны входных ( ) и выходных (
) и выходных ( ) полюсов.
) полюсов.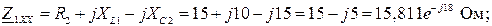

 и
и  .
. или
или 
 связаны между собой соотношением, которое называется уравнением связи:
связаны между собой соотношением, которое называется уравнением связи:
 и уравнение связи будет меть вид:
и уравнение связи будет меть вид:  .
. ;
;  ;
; 
 , а затем
, а затем :
:




 и активном сопротивлении нагрузки
и активном сопротивлении нагрузки  (подключено к клеммам
(подключено к клеммам 
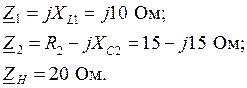
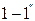 :
:

 на параллельном участке цепи:
на параллельном участке цепи: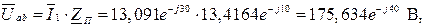 тогда
тогда




 равняется
равняется  . Выводы
. Выводы 



 называют коэффициентом передачи четырехполюсника, где
называют коэффициентом передачи четырехполюсника, где  - постоянная передачи (комплексная величина) – х
- постоянная передачи (комплексная величина) – х 


