
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Символический метод расчета цепей переменного токаСодержание книги
Поиск на нашем сайте
Из теории комплексных чисел известно, что всякое комплексное число а+jb может быть изображено геометрически в виде точки, имеющей две координаты (рис.14). Одна координата является отрезком а на вещественной оси (+I), а другая координата b – отрезком на мнимой оси (+j).
С другой стороны эти координаты являются проекциями вектора А, соединяющего начало координат с точкой, изображающей данное комплексное число а+jb. Величина этого вектора И, наконец, комплексное число может быть представлено в показательной (эйлеровой) форме: а+jb=Аеjφ, число еjφ указывает, на какой угол φ и в какую сторону повернут вектор данного комплексного числа по отношению к вещественной оси. Комплексные величины являются синусоидальными функциями времени (напряжение, ток) обозначают той же буквой, что и их модуль, но с точкой наверху; при обозначении других комплексных величин под буквой ставится горизонтальная черточка. Рассмотрим теперь, как можно представить синусоидально изменяющиеся величины в виде комплексных чисел. Возьмем простейшую цепь, состоящую из последовательно соединенных активного R и индуктивного XL сопротивлений. При построении векторной диаграммы цепи совместим ось абсцисс плоскости декартовых координат с вещественной осью комплексной плоскости. На векторной диаграмме вектор напряжения U разложим на составляющие: активную U = U cosφ и индуктивную UL =U sinφ.
В тригонометрической форме комплексы тока и напряжения будут выглядеть так: Ỉ = I и Ủ = U (cosj + j sinj).
В показательной форме: Ỉ = I и Ủ = Uejj
Приведенная запись синусоидально изменяющихся величин в виде комплексных изображений или символов называется символической, а действия над комплексами – символическим методом. Для последовательной цепи, состоящей из активного R и емкостного XC сопротивлений комплексы тока и напряжения можно записать в следующем виде:
Ỉ = I и Ủ = UА - jUC или Ủ = U (cosj + j sinj) или Ủ = Uejj, где
С помощью комплексных чисел аналитически выражают треугольники сопротивлений и проводимостей. Активные сопротивления и проводимости записывают действительной (вещественной) составляющей комплексного числа, реактивное – мнимой. Знак мнимой части отображает характер реактивного сопротивления: индуктивное сопротивление учитывается со знаком плюс, емкостное – со знаком минус. Так для цепи с последовательным соединением активного и индуктивного сопротивлений комплексное сопротивление Z =R+jXL или Z =Z еjφ, для цепи с последовательным соединением активного и емкостного сопротивлений – Z =R-jXC или Z =Z е –jφ. Мощность в цепи переменного тока также можно представить в виде комплексного числа. Напряжение на векторном участке цепи обозначим через Ủ = Uejj, ток на этом участке Ỉ = I ejj, угол между напряжением и током
Ŝ = Ủ Ỉ = UI ej(yu - yi) = UI ejj = UI cosj + jUI sinj = P + jQ. Значок ~ (тильда) над S обозначает, что речь идет о комплексе (а не о сопряженном комплексе) полной мощности, составленном при участии сопряженного комплекса тока I. Комплекс мощности Ŝ равен произведению прямого комплекса напряжения на сопряженный комплекс тока. Знак плюс у реактивной мощности соответствует индуктивному характеру сопротивления цепи, при емкостном характере был бы минус. Сформулируем закон Ома и Кирхгофа в символической форме: Закон Ома: Комплекс тока на участке цепи прямо пропорционален комплексу напряжения на нем и обратно пропорционален комплексу сопротивления: Ỉ = Ủ/ Z. Первый закон Кирхгофа: Алгебраическая сума комплексов токов в узле цепи равна нулю:
Второй закон Кирхгофа: В любом замкнутом контуре алгебраическая сума комплексов ЭДС равна алгебраической сумме комплексов напряжений на его участках:
При использовании законов Ома и Кирхгофа в символической форме появляется полная аналогия в метод расчета цепей переменного и постоянного тока; все методы расчета электрических цепей постоянного тока применимы в символической форме к расчетам цепей переменного тока. Задача №2 Задание
Электрическая цепь переменного синусоидального тока с частотой
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 244; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.202.168 (0.006 с.) |



 называется модулем данного числа. Это же комплексное число может быть представлено в тригонометрической форме а+jb=A(cosφ+j sinφ).
называется модулем данного числа. Это же комплексное число может быть представлено в тригонометрической форме а+jb=A(cosφ+j sinφ).
 . Умножим комплекс напряжения на сопряженный комплекс тока Ỉ = I ejj и обозначим полученный комплекс через Ŝ:
. Умножим комплекс напряжения на сопряженный комплекс тока Ỉ = I ejj и обозначим полученный комплекс через Ŝ:




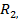


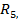

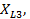
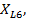

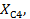



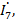


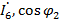




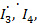
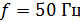 , находящаяся под действием напряжения U, содержит активные сопротивления
, находящаяся под действием напряжения U, содержит активные сопротивления  , реактивные индуктивные
, реактивные индуктивные  и реактивные емкостные
и реактивные емкостные  сопротивления. По данным таблицы с учетом положения выключателей В1 - В7 определить для данного варианта задания приведенные в ней величины. Проверить токи по 1 – му закону Кирхгофа, проверить соблюдение баланса полных S, активных P и реактивных Q мощностей, построить векторную диаграмму напряжений и токов.
сопротивления. По данным таблицы с учетом положения выключателей В1 - В7 определить для данного варианта задания приведенные в ней величины. Проверить токи по 1 – му закону Кирхгофа, проверить соблюдение баланса полных S, активных P и реактивных Q мощностей, построить векторную диаграмму напряжений и токов.



