
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет сложных электрических цепей методом непосредственного применения законов КирхгофаСодержание книги
Поиск на нашем сайте
Расчёт сложных цепей состоит в определении неизвестных токов при заданных значениях ЭДС всех источников и сопротивлений всех участков цепи. Расчёт производится в следующей последовательности: 1) На всех участках цепи стрелками указываются произвольные направления токов. Если направления каких-либо токов будет указано неправильно, то при окончании решения эти токи получатся со знаком минус. 2) Для узлов цепи записываются уравнения первого закона Кирхгофа. Если цепь содержит n узлов, записывается (n-1) уравнений. 3) Для замкнутых контуров записываются уравнения второго закона Кирхгофа. Чтобы эти уравнения были независимыми, необходимо следить за тем, чтобы в контуре, для которого записывается уравнение, содержался, хотя бы один участок, не входящий в другие контуры. Например, для схемы (рис. 1.) можно записать три уравнения по первому закону Кирхгофа и три – по второму закону Кирхгофа. для узла 1: I1-I2+I3=0; для узла 2: I2+I6-I5=0; для узла 3: I5-I3-I4=0; для контура 4-1-2-4: E1 – E2 = I1R1 + I2R2 – I6R6; для контура 1-2-3-1: E3 – E2 = I3R3 + I2R2 + I5R5; для контура 4-3-2-4: 0 = I4R4 + I5R5 + I6R6. 4) Обходя контур в направлении контурного тока, составляют для каждого контура уравнение по второму закону Кирхгофа с учётом как контурного тока данного, так и контурных токов смежных контуров. 5) Решая полученную систему уравнений, определяют контурные токи. Действительные токи во всех внешних ветвях равны контурным токам, токи в смежных ветвях равны разности контурных токов смежных контуров. Например, для схемы рис. 1 можно записать следующие три уравнения: для контура 4-1-2-4: E1-E2 =I11(R1+R2+R6)-I22R2-I33R6; для контура 1-3-2-1: E2-E3 =I22(R2+R3+R5)-I11R6-I22R5; для контура 4-2-3-4: 0 =I33(R4+R6+R5)-I11R6-I22R5. Действительные токи: I1 = I11; I3 = I22; I4 = I33; I2 = I11 + I22; I5 = I33 + I22; I6 = I33 – I11. Для проверки правильности решения системы, подставляем найденные значения токов ветвей в уравнения по первому и второму законов Кирхгофа. Уравнение баланса мощности для схемы будет иметь следующий вид: E1I1 – E2I2 + E3I3 = I12R1 + I22R2 + I32R3 + I42R4 + I52R5 + I62R6 Задача №1 Задание
Для электрической цепи постоянного тока, используя данные, приведенные для своего варианта задания в таблице, определить токи
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА Переменный ток в цепи с активным сопротивлением Предположим, что к цепи приложено синусоидальное напряжение (для простоты считаем начальную фазу напряжения равной нулю): e = EМ sin α Необходимо установить, как будет изменяться ток цепи. В соответствии с законом Ома мгновенное значение тока I = EМ / R 0+R Если обе части выражения для амплитуды тока разделить на Эта формула выражает закон Ома для цепи с резистивным элементом.
1. Ток в цепи с резистивным элементом изменяется по закону синуса; 2. Ток в цепи с резистивным элементом совпадает по фазе с напряжением. Синусоидальная и векторная диаграммы цепи показаны соответственно (рис. 2, б, в). Переменный ток в цепи с индуктивным сопротивлением Предположим, что в катушке (рис. 3, а) приложено синусоидальное напряжение u = UМ sin ωt. Тогда ток в цепи изменяется по закону i = IМ sin (wt - p/2). Действующее значение тока определяется I = U / wL. Размерность ωL, стоящей в знаменателе
На основании этого величина ωL называется индуктивным сопротивлением и обозначается XL XL = ωL=2πf·L. Таким образом, закон Ома для цепи с индуктивностью выражается следующим образом I=U/ХL.
Ток в цепи с индуктивность отстает по фазе от напряжения на угол π/2 (90o,1/4T).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 261; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.198.181 (0.006 с.) |


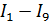 в ветвях резисторов
в ветвях резисторов  методом контурных токов. Составить баланс мощностей. Внутренним сопротивлением источников пренебречь.
методом контурных токов. Составить баланс мощностей. Внутренним сопротивлением источников пренебречь.
 , получим выражение для действующего значения тока: I = U/R.
, получим выражение для действующего значения тока: I = U/R.
 .
.



