Собственная проводимость полупроводников

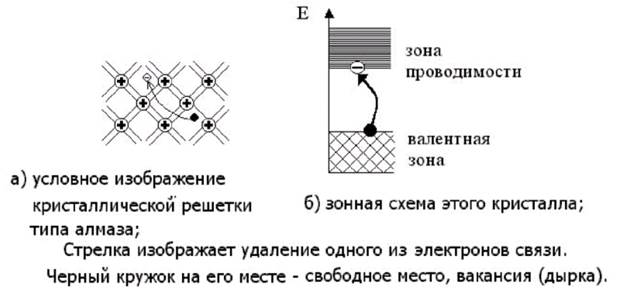
Из элементов таблицы Менделеева типичными полупроводниками являются германий и кремний. Ширина запрещенной зоны у германия 0,66эВ, у кремния - 1,1эВ (при T = 300К).

Имея по 4 валентных электрона, атомы Ge и Si образуют кристаллические решетки типа алмаза, где каждый атом имеет 4 ближайших соседа, с каждым из которых он связан ковалентной связью.

Условно пространственное расположение атомов в решетке типа алмаза можно представить в виде плоской структуры (см. рисунок 13.8а).

Рис. 13.8

При достаточно высокой температуре тепловое движение способно разорвать некоторые связи, удалив электрон в то место кристалла, где все связи заполнены (рис.13.8а). Там электрон будет лишним. Такой электрон в дальнейшем свободно может двигаться по кристаллу, всюду являясь лишним. На рис. 13.8б) тот же процесс разрыва одной связи изображен на зонной схеме полупроводника: электрон из валентной зоны перешел в свободную зону (зону проводимости для полупроводника). Там, в зоне проводимости, электрон, как мы выше выяснили, может двигаться под действием сколь угодно малого внешнего электрического поля - создавать электрический ток. Отметим, что электрон в зоне проводимости ведет себя как частица с эффективной массой m*, не равной массе электрона (m* ≠ m_e = 9,1·10^-31 кг).

При разрыве одной связи (удаление с нее одного электрона) на месте этой связи останется нескомпенсированный положительный заряд. На зонной схеме эта ситуация изображается освобождением одного состояния в валентной зоне, до этого полностью заполненной. Такие незанятые электронами (вакантные) состояния называют дырочными состояниями. Дырки ведут себя как частицы с положительным зарядом, равным заряду электрона.

Во внешнем поле они двигаются в направлении вектора напряженности электрического поля, как частицы с эффективной массой m* > 0.

Если электрон проводимости, блуждая по кристаллу, встретит дырку (частично разорванную связь), то связь заполнится этим электроном. При этом число электронов проводимости уменьшится на единицу, одновременно станет на единицу меньше и число дырок. Этот процесс называется рекомбинацией носителей. Он изображен на рисунках 13.9.

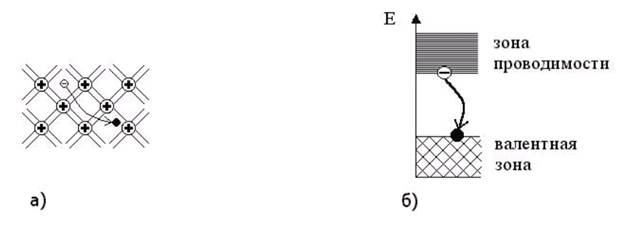
Рис. 13.9

На рисунке 13.9а) электрон проводимости заполняет незанятое место в ковалентной связи. На зонной схеме 13.9б) этому процессу соответствует переход электрона из зоны проводимости в вакантное состояние (дырку) валентной зоны.

Как видно из рисунка 13.9б), энергия электрона проводимости в процессе рекомбинации уменьшается. Избыток энергии может выделиться в виде излучения (излучательная рекомбинация). Возможна безизлучательная рекомбинация, при которой энергия выделяется в виде колебаний решетки или передается другим электронам проводимости, либо дыркам. Излучательная рекомбинация лежит в основе действия полупроводниковых лазеров.

При заданной температуре устанавливается равновесие между процессом образования электронно-дырочных пар и процессом их рекомбинации. Таким образом устанавливается равновесное для заданной температуры число носителей зарядов.

Проводимость, возникающая за счет переходов под действием температуры электронов идеального кристалла полупроводника из валентной зоны в свободную (зону проводимости), называется собственной проводимостью полупроводника.

С ростом температуры растет равновесное число электронов в зоне проводимости и число дырок в валентной зоне. При этом в идеальном кристалле число образовавшихся электронов проводимости равно числу появившихся дырок. Эти электроны и дырки являются носителями тока. Удельная проводимость σ пропорциональна концентрации носителей n (см. (12.2)). Следовательно, удельная проводимость полупроводников будет расти с температурой.

Распределение электронов по уровням зоны проводимости и валентной зоны описывается функцией Ферми-Дирака f(E) (11.4), причем у полупроводников с собственной проводимостью уровень Ферми E_F с большой точностью расположен посредине запрещенной зоны. На рисунке 13.10 график f(E) изображен рядом с энергетической схемой полупроводника.

Из рисунка 13.10 видно, что для электронов, находящихся у "дна" зоны проводимости:

Рис. 13.10

Если что обычно и имеет место. Тогда мы имеем дело с "хвостом" функции f(E) (11.5); учитывая (13.2), получим:

Концентрация электронов проводимости n (и равная ей концентрация дырок) будет пропорциональна f(E), а так как проводимость σ пропорциональна концентрации, то для нее, с учетом (13.3), имеем:

Переходя от пропорциональности к равенству, получим формулу зависимости собственной проводимости полупроводников от температуры:

здесь σ₀ - постоянная величина, имеющая размерность проводимости.

Из полученной формулы видно, что собственная проводимость полупроводников σ экспоненциально быстро растет с температурой.

Изучая на опыте зависимость σ(Т), можно найти экспериментальное значение ширины запрещенной зоны ΔE_зап.

В полупроводниках и диэлектриках электроны могут перейти из валентной зоны в зону проводимости за счет поглощения фотонов, энергия которых достаточна для обеспечения такого перехода. Энергия фотона ε, как известно, равна hν. Значит необходимым условием внутреннего фотоэффекта является неравенство:

В результате внутреннего фотоэффекта возникает собственная фотопроводимость. Измеряя граничную частоту ν_кр (или соответствующую ей длину волны λ_кр=с/ν_кр), т.е. определяя красную границувнутреннего фотоэффекта, можно найти ширину запрещенной зоны полупроводника или диэлектрика:

Итоги лекции N 13

1. При объединении атомов в кристалл их энергетические уровни вследствие принципа Паули превращаются в систему очень близко расположенных подуровней - разрешенныеэнергетические зоны. Разрешенные зоны могут быть разделены запрещенными зонами, электрон не может иметь энергию, лежащую в пределах запрещенной зоны.
2. Если самая верхняя - валентная - зона заполнена наполовину, то она является зоной проводимости. Такие кристаллы относятся к металлам. Все металлы хорошо проводят электрический ток.
3. Если валентная зона заполнена полностью, а следующая за ней разрешенная зона отделена от валентной широкой запрещенной зоной (ΔE_зап ≈ 10 эВ), то такой кристалл будет диэлектриком. Диэлектрики почти не проводят электрический ток.
4. Полупроводники имеют зонную схему, похожую на зонную схему диэлектриков, но ширина запрещенной зоны у них мала (ΔE_зап ≤ 3 эВ). Поэтому при нагревании часть электронов переходит из валентной зоны в свободную зону, которая и является у полупроводников зоной проводимости. Проводимость беспримесных полупроводников экспоненциально растет сростом температуры. Такая проводимость называется собственной проводимостью полупроводников.
5. Если электроны в полупроводниках переходят из валентной зоны в зону проводимости за счет поглощения фотонов с энергией hν ≥ ΔE_зап, то возникает собственная фотопроводимость. Это явление называется внутренним фотоэффектом.

 

ЛЕКЦИЯ N 14

Примесная проводимость полупроводников. Донорные примеси, полупроводники n-типа. Акцепторные примеси, полупроводник р-типа. Электронно-дырочный переход, полупроводниковый диод. Полупроводниковый триод (транзистор)