Электронный газ в модели одномерной бесконечно глубокой ямы

Поведение одной частицы в бесконечно глубокой одномерной яме было разобрано в § 3 лекции N 7. Теперь мы хотим разместить в этой яме N свободных электронов. При этом взаимодействием между электронами мы пренебрегаем, но обязательно должны учесть принцип Паули (§ 1, лекция 9). В нашем случае квантовыми числами, задающими состояние электрона, будут n и спиновое квантовое число m_s, которое для электрона может принимать два значения, m_s = ±1/2. Принцип Паули утверждает, что в одномерной яме не может быть двух электронов с одинаковыми квантовыми числами n и m_s. Так как m_s принимает два значения, то на каждом энергетическом уровне в одномернойяме сможет разместиться не больше двух электронов.

Уровень энергии, отвечающий различным квантовым состояниям, называется вырожденным. В одномерной потенциальной яме все уровни двукратно вырождены.

На рисунке 10.1 изображена одномерная, бесконечно глубокая потенциальная яма, в которой размещены шесть электронов (N = 6) при T = 0. Первые три энергетических уровня заняты, все остальные, начиная с четвертого (n = 4) - свободны.

Рис. 10.1

Энергия Ферми E_F(0) - это энергия электронов на высшем, еще заполненном уровне при T = 0.

На нашем рисунке 10.1 энергия Ферми при N = 6 равна энергии третьего энергетического уровня. В реальных ситуациях число электронов N имеет порядок числа Авогадро (см. Ч. 4, лекция 1, § 1), т.е. N ~ N_A. Выражение для энергии Ферми при T = 0, E_F(0), получим, приравняв квантовое число n в формуле (7.21) для энергии стационарных состояний частицы в одномерной бесконечно глубокой потенциальной яме половине числа частиц, т.е. n = N/2 (т.к. на каждом уровне - два электрона). Тогда получим:

Как мы видим, энергия Ферми при T = 0, E_F(0) зависит от числа занятых электронами состояний. В одномерной яме число занятых состояний N (одно состояние - один электрон) (!) равно удвоенному значению квантового числа n. В других ситуациях подсчет числа состояний, доступных микрочастицам, более сложен. Так в трехмерной яме кратность вырождения, т.е. число квантовых состояний, соответствующих заданному значению энергии, растет с ростом энергии. Объясняется это тем, что энергия частицы Е - величина скалярная, а импульс - векторная, как известно . При заданном значении модуля импульса р (а следовательно и энергии Е) направление вектора импульса может быть различным. При этом, как будет показано ниже, число состояний Z, для которых модуль импульса р меньше заданного значения, растет пропорционально третьей степени р. Подсчет числа этих состояний нужен для определения Е_F (0) энергии Ферми для более реалистической модели трехмерной потенциальной ямы. Проще всего этот подсчет выполнить, используя понятия фазового µ-пространства и фазовой ячейки.

Фазовое µ - пространство - это воображаемое шестимерное пространство со взаимно перпендикулярными осями x, y, x, p_x, p_y, p_z.

Для задания состояния рассматриваемой системы частиц в классической физике также вводят фазовое пространство, объединяющее координаты и импульсы всех частиц системы.

Рис. 10.2

Для частицы, совершающей одномерное движение (частица в одномерной яме), фазовое µ-пространство представляет из себя две взаимно-перпендикулярные оси, по которым откладывается координата x и соответствующий ей импульс p. В квантовой механике появляются ограничения на возможные значения импульса, связанные с квантованием волнового числа k. Для частицы в яме шириной a в соответствии с формулой (7.20):

Так как по соотношению де Бройля (6.1)

то импульсы тоже квантуются:

Здесь

Как отмечалось в § 3 лекции N 7 положительные и отрицательные числа n соответствуют одному и тому же стационарному состоянию, но в фазовом µ-пространстве положения точек, имеющих разные по знаку импульсы, будут разными. Объемом нашего двухмерного пространства ΔГ называют произведение ΔpΔx, т.е.

здесь Δp - интересующий нас интервал изменения импульса, а Δx - интервал изменения координаты.

Найдем ΔГ_эл - элементарный объем, занимаемый в фазовом пространстве одним квантовым состоянием частицы, находящейся в одномерной бесконечно глубокой яме (спиновое квантовое число здесь не учитывается). Из рисунка 10.2 видно, что для одного квантового состояния.

Двойка появляется из-за того, что одному состоянию соответствуют два значения импульса, отличающиеся знаком.

Очевидно, что Δx = a, тогда

Таким образом, одно квантовое состояние частицы, находящейся в одномерной бесконечно глубокой потенциальной яме, занимает в фазовом µ-пространстве одну элементарную ячейку размером h (без учета спина!).

Для подсчета числа квантовых состояний ΔZ в фазовом объеме ΔГ очевидно необходимо поделить фазовый объем ΔГ на объем элементарной ячейки h и умножить, для учета двух направлений спина, на два:

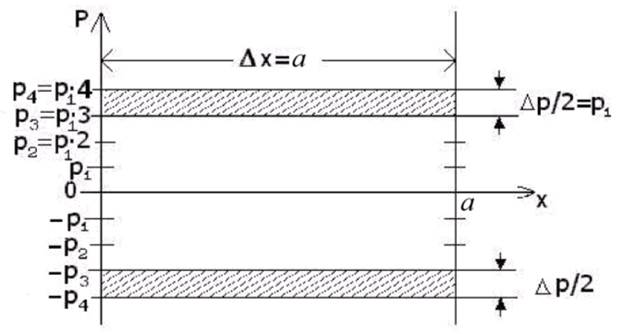
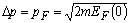Из формулы (10.3) нетрудно получить формулу (10.1), для этого надо положить , Δx = a и учесть, что