Введение в зонную теорию твердых тел

 

ЛЕКЦИЯ N 13

Происхождение энергетических зон в кристаллах. Металлы, диэлектрики и полупроводники в зонной теории. Собственная проводимость полупроводников

Зонная теория твердых тел - квантовая теория энергетического спектра электронов в кристалле, согласно которой этот спектр состоит из чередующихся зон разрешенных и запрещенных энергий. Зонная теория объясняет, в частности, различный характер электропроводности металлов, полупроводников и диэлектриков.

§ 1. Происхождение энергетических зон в кристаллах. Металлы

Физически происхождение зонной структуры в кристалле связано с образованием кристалла из N атомов, каждый из которых в свободном состоянии обладает дискретным электронным энергетическим спектром (см. лекцию N 9, § 2).

Мы рассмотрим образование энергетических зон на примере воображаемого процесса образования кристалла лития (щелочной металл) путем последовательного добавления атомов.

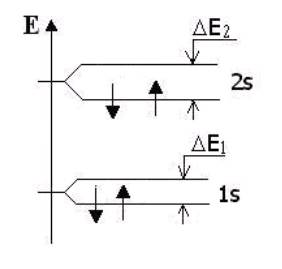
Рис. 13.1

На рис. 13.1 изображены схемы энергетических уровней двух изолированных атомов.

Если атомы расположены далеко друг от друга (изолированы), то схемы их энергетических уровней будут совершенно одинаковы: два электрона с различной ориентацией спинов на уровнях 1s и по одному электрону на уровнях в 2s (рис. 13.1).

При сближении двух атомов на расстояние, где их взаимодействием уже нельзя пренебречь, энергетическая схема должна измениться: иначе мы придем в противоречие с принципом Паули. Так при неизменной энергетической схеме на уровне 1s было бы уже по два электрона в одном квантовом состоянии: два со спином вверх и два со спином вниз. Принцип Паули приводит к появлению новых состояний: энергетические уровни расщепляются на два подуровня. Теперь на подуровнях 1s, в полном соответствии с принципом Паули, разместились четыре электрона, по одному в каждом квантовом состоянии. На рис. 13.2 изображена энергетическая схема системы из двух атомов.

Рис. 13.2

Обратим внимание на то, что верхний подуровень 2s оказался свободным. Величина расщепления уровней ΔE зависит от расстояния между атомами. При сближении атомов ΔE растет.

Величина ΔE₁ < ΔE₂, так как в состоянии 1s электроны сильнее связаны с ядром, чем в состоянии 2s.

Добавим в наш кристалл еще один атом. На рис. 13.3 изображены энергетическая и пространственная схемы системы из трёх атомов.

Рис. 13.3

Как видно из пространственной схемы, изображенной на рис. 13.3, минимальное расстояние между атомами - постоянная кристаллической решетки a - осталось неизменным. Значит величина расщепления (ΔE₁ и ΔE₂) будет той же самой, как и для системы из двух атомов (ΔE зависит от минимального расстояния между атомами). Третий энергетический уровень расположился между двумя крайними.

Продолжая добавлять в нашу систему атомы и рассуждая аналогично, мы придем к выводу, что для системы из N атомов каждый из уровней изолированного атома расщепляется на N подуровней (рис. 13.4). При этом величина расщепления ΔE не будет зависеть от числа атомов, так как минимальное расстояние между атомами в кристалле остается неизменным. Следовательно, расстояние соседними подуровнями будет уменьшаться с ростом N - числа атомов в кристалле. Число атомов N имеет порядок числа Авогадро N_A = 6,02·10²³1/моль.

Максимальное расщепление уровней ΔE по порядку величины составляет 1 эВ, значит:

Энергетическая схема системы, состоящей из N атомов лития, изображена на рис.13.4

Рис. 13.4

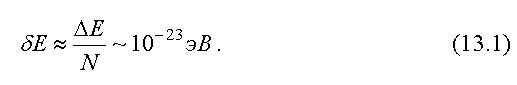
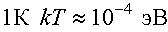Это очень малая величина по сравнению с величиной kT - добавкой энергии, которую в среднем получает электрон при нагревании. Так, при температуре , что почти на два десятка порядков (!) больше чем δE. Поэтому можно считать, что энергия в такой системе очень близко расположенных подуровней меняется почти непрерывно (квазинепрерывно). Систему подуровней называют разрешенной зоной. В кристалле лития образовалось две разрешенных зоны: из 1s и 2s уровней изолированного атома. Зона, получившаяся из 1s уровня, полностью заполнена. Зона, образовавшаяся из валентного 2s уровня, заполнена наполовину (на наших схемах заполнение обозначено штриховкой в клеточку). Между этими зонами находится интервал энергий, запрещенных для электронов: это - запрещенная зона, ее ширину мы обозначаем ΔE_зап.

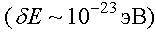Нетрудно понять, что кристалл с подобной зонной схемой (см. рис. 13.4) будет хорошо проводить электрический ток: электроны наполовину заполненной зоны могут под действием внешнего электрического поля увеличивать свою энергию квазинепрерывным образом . Увеличение энергии при приложении внешнего электрического поля связано с возникающим упорядоченным движением электронов - электрическим током. Все металлы хорошо проводят электрический ток, так как имеют энергетическую схему подобную, только что рассмотренной схеме кристалла лития (см. рис. 13.4).