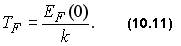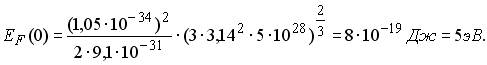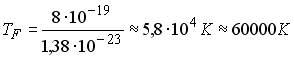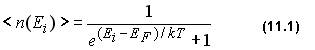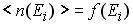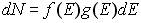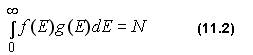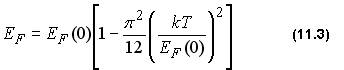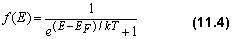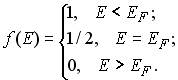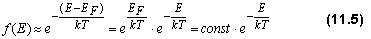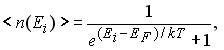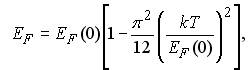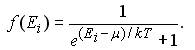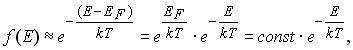Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электронный газ в модели бесконечно глубокой трехмерной потенциальной ямыСодержание книги
Поиск на нашем сайте
Перейдем к описанию электронов в модели трехмерной потенциальной ямы. В первом приближении ее можно считать бесконечно глубокой. Пусть образец имеет форму прямоугольного параллелепипеда с размерами Δx, Δy, Δz. В трехмерном случае фазовое m-пространство для частицы - это шестимерное пространство, по осям которого откладываются три координаты x, y, z и три компоненты импульса px, py, pz частицы. Объем фазового пространства кубической формы
Для числа состояний ΔZ в трехмерном случае имеем:
Теперь определим энергию Ферми в трехмерной яме. Как и в одномерном случае энергия Ферми EF(0) - это энергия электронов на высшем еще заполненном уровне при T = 0. При T = 0 в соответствии с принципом Паули (лекция N 9, § 1) каждое квантовое состояние с E < EF(0) будет занято одним из общего числа N электронов. Значит, для нахождения EF(0), нам надо найти зависимость числа состояний ΔZ от энергии E, затем приравнять число состояний с энергией E ≤ EF(0) числу частиц и выразить из этого равенства EF(0). Реализуем последовательно эту программу. Число состояний ΔZ в фазовом объеме ΔГ определяется формулой (10.5). Фазовый объем ΔГ состояний с импульсом p < pF(0) определим из следующих соображений. Так как полная энергия E электронов внутри потенциальной ямы равна кинетической, то
Значит состояния с E ≤ EF(0) - это состояния, у которых модуль импульса электронов лежит в пределах от нуля до В подпространстве импульсов этим состояниям соответствует сфера радиусом pF(0). Умножив "объем" этой сферы на объем ямы V получим интересующий нас объем фазового пространстве ΔГ, т.е.
Из (10.5) и (10.6) получим число состояний ΔZ(p) с учетом спина:
Выразим pF(0) через EF(0). Т.к.
откуда для числа состояний ΔZ(E) с энергией меньше, чем EF(0):
В дальнейшем нам потребуется выражение для числа состояний на единичный энергетический интервал - плотность состояний g(E). Очевидно, что
Продифференцировав по ЕF формулу (10.7), получим
Здесь мы заменили ЕF на Е, Приравняв ΔZ(EF) (10.7) числу электронов в яме N, получим
Выразим отсюда EF(0):
здесь Выразив h через
Температурой Ферми TF - называют отношение энергии Ферми EF(0) к постоянной Больцмана k, т.е.
Оценим энергию Ферми EF(0) и температуру ФермиTF. Концентрация свободных электронов в металле порядка 1028÷1029 м-3. Для n = 5·1028 м-3 из (10.8) получим:
Для TF из (10.9) получим:
Итоги лекции N 10 1. Поведение валентных электронов в металлах можно объяснить на основе модели потенциальной ямы. При низких температурах, когда тепловое движение не способно удалить электроны из металла, потенциальную яму можно читать бесконечно глубокой. 2. При Т = 0 учет принципа Паули приводит к последовательному увеличению энергии электронов при заполнении ими квантовых состояний. 3. Энергия Ферми EF(0) - это энергия электронов на высшем, еще заполненном уровне при Т = 0 К. 4. Квантовая теория свободных электронов в металле для модели трехмерной потенциальной ямы (см. § 2) дает следующую формулу для энергии Ферми (см (10.10)):
здесь 5. Оценки дают для EF(0) значение около 5 эВ.
ЭЛЕМЕНТЫ КВАНТОВОЙ СТАТИСТИКИ ЛЕКЦИЯ N 11 Электронный газ при Т > 0. Распределение Ферми-Дирака. Анализ функции f(Е) § 1. Электронный газ при T > 0. Распределение Ферми-Дирака
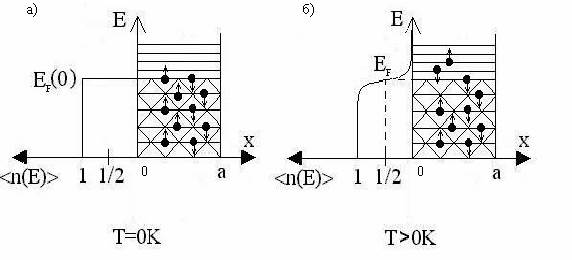
Рис. 11.1 На приведенных выше рисунках 11.1 изображена одномерная потенциальная яма, заполненная электронным газом; на рис. а) при T = 0, на рис. б) при T > 0. Слева от потенциальной ямы изображены графики зависимости среднего по времени числа электронов в одном квантовом состоянии - <n(E)> - от энергии электронов E. Энергия E отложена по вертикальной оси, проходящей вдоль левой границы ямы, сама функция <n(E)> отложена по горизонтальной оси, направленной влево. При T = 0K электроны занимают все доступные им состояния с наинизшей энергией. В соответствии с принципом Паули в каждом квантовом состоянии может находиться не более одного фермиона, поэтому все нижние квантовые состояния до энергии EF(0) заняты. Таким образом, график функции <n(E)> представляет из себя ступеньку: <n(E)> = 1 при E < EF(0) и <n(E)> = 0 при E > EF(0). При нагревании металла часть электронов, энергия которых была близка к энергии Ферми, переходят в состояния с большей энергией, частично освобождая квантовые состояния с энергией E < EF(0): ступенька графика <n(E)> размывается. Аналитическую зависимость среднего числа ферминов в одном квантовомсостоянии от их энергии и температуры получили итальянский физик Э. Ферми и английский физик П. Дирак. Она имеет следующий вид:
и называется распределением Ферми-Дирака. Параметр EF, входящий в распределение Ферми-Дирака, называется уровнем Ферми. В статистической физике этот параметр называется химическим потенциалом, его обозначают буквой µ, таким образом µ ≡ EF. Среднее число электронов в одном квантовом состоянии <n(E)> изменяется от нуля до единицы, в этих же пределах изменяется вероятность f(Ei) заполнения данных квантовых состояний. Таким образом
С учетом того, что EF ≡µ, функцию распределения Ферми-Дирака можно записать в таком виде:
Значение уровня Ферми EF (или химического потенциала µ) определяют из условия нормировки функции f(Ei): полное число электронов, находящихся во всех квантовых состояниях должно быть равно числу N свободных электронов в рассматриваемом объеме V. Среднее число электронов в одном квантовом состоянии дается функцией Ферми-Дирака f(Ei) (11.1а). Так как расстояния между соседними уровнями при макроскопических объемах образца малы, то можно считать, что энергия меняется непрерывным образом, т.е. f(Ei) → f(E). Число квантовых состояний, приходящихся на интервал энергий dE получим, умножив плотность состояний g(E) (10.9) на dE. Число электронов dN, имеющих энергию в интервале от E до E+dE, получим, умножив f(E) на g(E)dE, т.е.
Наконец, проинтегрировав dN, получим N - полное число электронов в образце:
Это и есть условие нормировки функции распределения Ферми-Дирака. Значение EF (или химический потенциал µ) можно найти, подставив в условие нормировки (11.2) f(E) из (11.1а) и g(E) из (10.9). Однако аналитическое выражение для получающегося интеграла отсутствует. При не очень высоких температурах, таких, что kT << EF, для уровня Ферми получается приближенное выражение:
Здесь EF(0) определяется формулой (10.9). §2. Анализ функции f(E) Выпишем функцию распределения Ферми-Дирака в следующем виде:
Нетрудно убедиться, что при E = EF функция f(E) = 1/2. Поведение функции f(E) (и электронного газа в металле) зависит от соотношения между температурой металла T и температурой Ферми (10.11). При T << TF (т.е. kT << EF) электронный газ называют вырожденным и график функции f(E) незначительно отличается от ступени. В самом деле, показатель экспоненты (E - EF) / kT будет велик по модулю всюду, за исключением интервала энергий, в котором (E - EF) ≤ kT. При этом, если E < EF, то (E - EF) / kT будет величиной отрицательной и большой по модулю, значит экспонента будет близка к нулю, а f(E) ≈ 1. В случае, если E > EF, показатель экспоненты будет большой положительной величиной и f(E) ≈ 0. Запишем результаты анализа в следующем виде:
Из оценок, сделанных в § 2 лекция 10, TF ≈ 60000K, значит вплоть до Tпл - температуры плавления металлов, электронный газ вырожден (самый тугоплавкий металл, вольфрам, имеет Tпл ≈ 3693K). При T >> TF электронный газ называется невырожденным. В этом случае график функции f(E) идет полого спадая и уже совсем не похож на ступеньку. На рисунке 11.2 приведены графики функции f(E) (11.4) для различных температур.
Рис. 11.2 При больших значениях энергии электронов, таких, что E - EF >> kT, единицей в знаменателе функции f(E) (11.4) можно пренебречь, тогда для "хвоста " функции f(E) справедлива следующая формула:
что совпадает с распределением Максвелла-Больцмана (см. Ч. 3, (2.14)). Итоги лекции N 11 1. Зависимость среднего числа фермионов в одном квантовом состоянии <n(Ei)> от их энергии и температуры называется распределением Ферми-Дирака (см. (11.1)):
здесь ЕF - уровень Ферми, параметр распределения, который определяют из условия нормировки. Другое название этого параметра - химический потенциал, который принято обозначать греческой буквой µ, т.е. EF ≡ µ. 2. При не очень высоких температурах, когда kT<<EF для уровня Ферми справедливо приближенное выражение (см. (11.3)):
здесь EF(0) - энергия Ферми. 3. Так как среднее число фермионов в одном квантовом состоянии изменяется от 0 до 1, т.е. в тех же пределах, что и вероятность f(Ei) заполнения данных квантовых состояний, то для f(Ei) справедлива формула (11.1а), аналогичная формуле (11.1):
4. Анализ функции f(E) при Т=0 К дает следующие результаты:
5. При больших значениях энергии электронов, таких, что Е-ЕF>>kT, для "хвоста" функции f(Е) справедлива формула (11.5):
что совпадает с распределением Максвелла-Больцмана.
ЛЕКЦИЯ N 12
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1139; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.108.134 (0.008 с.) |

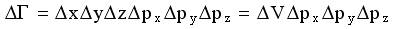 , здесь ΔV - обычный пространственный объем области, в которой находится частица. Объем элементарной фазовой ячейки в трехмерном случае можно найти из соображений, аналогичных тем, что были изложены выше для одномерного случая. В результате получим, что
, здесь ΔV - обычный пространственный объем области, в которой находится частица. Объем элементарной фазовой ячейки в трехмерном случае можно найти из соображений, аналогичных тем, что были изложены выше для одномерного случая. В результате получим, что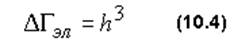
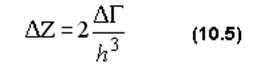

 (10.6)
(10.6)
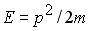 , то
, то
 (10.7)
(10.7) (10.8)
(10.8)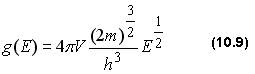
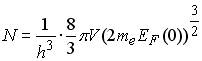
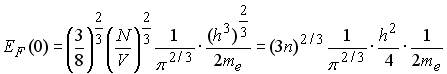
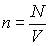 - концентрация электронов.
- концентрация электронов.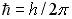 , получим окончательную формулу для EF(0) - энергии Ферми для электронного газа в трехмерной потенциальной яме:
, получим окончательную формулу для EF(0) - энергии Ферми для электронного газа в трехмерной потенциальной яме: