
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Спектры атома водорода в теории ШредингераСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Появление в шредингеровской теории атома водорода, в отличие от теории Бора, квантования момента импульса L и его проекции Lz объясняет некоторые особенности спектров излучения и поглощения атома водорода, которые не могли быть объяснены теорией Бора. Для пояснения этих особенностей изобразим схему уровней атома водорода, на которой учтено вырождение уровней по азимутальному квантовому числу l, (см. рис. 8.2).
Рис. 8.2 На приведенной схеме по вертикали отложена полная энергия En электрона в атоме водорода, выраженная в электронвольтах и значения главного квантового числа n. По горизонтали отложены дискретные значения азимутального квантового числа l вместе с их спектроскопическими обозначениями. Линии, соединяющие энергетические уровни, обозначают разрешенные правилом отбора переходы электрона с одного энергетического уровня на другой. При этом или испускаются или поглощаются фотоны соответствующих энергий ε = En - Em. Правило отбора связано с тем, что фотон обладает собственным моментом импульса. При излучении света фотон уносит момент импульса из атома, а при поглощении - приносит. Поэтому, вследствие закона сохранения момента импульса, момент импульса атома в процессах излучения и поглощения фотонов изменяется. Оказывается, с наибольшей интенсивностью идут такие переходы, в которых выполняется следующее правило отбора:
Это правило отбора справедливо для так называемых дипольных переходов. Оно запрещает, например, дипольный переход электрона из состояния 2s в состояние 1s, разрешенный законом сохранения энергии. Поэтому электрон может сравнительно долго находиться в состоянии 1s, если он туда попадает. Такое состояние называется метастабильным. Так как стационарные значения энергии атома водорода в теории Бора и в теории Шредингера совпадают, то в первом приближении из теории Шредингера следуют такие же спектры излучения и поглощения, как и в теории Бора. Однако, шредингеровская теория атома водорода позволяет учесть влияние на энергетические уровни взаимодействия орбитального и спинового моментов импульса электрона (тонкая структура спектра). Кроме того шредингеровская теория позволяет учесть влияние на спектры магнитного поля (эффект Зеемана) и электрического поля (эффект Штарка). Учет взаимодействия спиновых магнитных моментов ядра и электрона приводит к сверхтонкому расщеплению уровня 1s атома водорода на два подуровня. Переход электрона между этими подуровнями приводит к излучению (или поглощению) радиоволн с длиной волны λ = 21 см. Такое излучение испускается межзвездным водородом в галактиках. Изучая это излучение с помощью радиотелескопов, астрономы получают много полезной информации. Волновая функция основного состояния атома водорода Для основного состояния атома водорода квантовые числа n, l, m l имеют следующие значения: n = 1, l = 0, m l = 0. Это состояние обозначают 1s. Уравнение Шредингера имеет для 1s состояния решение ψnim = ψ100 которое зависит только от расстояния r между ядром и электроном:
Здесь В соответствии с вероятностным смыслом волновой функции вероятность dw обнаружить электрон в объеме dV:
Отметим, что dw зависит от выбранной нами формы элементарного объема dV. Если взять dV в форме прямоугольного параллелепипеда, т.е. dV = dxdydz и обозначить через dw соответствующую вероятность, то
В этом случае плотность вероятности обнаружить электрон в объеме параллелепипеда dV = dxdydz будет равна
Плотность вероятности имеет максимальное значение (1/π03) при r = 0, график этой функции изображен на рисунке 8.3.
Рис. 8.3. Так как волновая функция 1s состояния зависит только от r, то обычно элемент объема dV берут в виде сферического слоя радиуса r и толщиной dr. Как известно из геометрии, объем такого сферического слоя dV = 4πr2dr. Обозначим через dw0 соответствующую вероятность, тогда
Эта функция равна нулю при r = 0 и r → ∞. При r = r0 она имеет максимум, положение которого соответствует первой боровской орбите.
Рис. 8.4 Итоги лекции N 8 1. Формула (8.3) для энергии стационарных состояний атома водорода, полученная на основе уравнения Шредингера совпадает с аналогичной формулой (4.8), полученной в боровской теории атома водорода, т.е.:
Здесь n называется главным квантовым числом. 2. Волновые функции ψnlm(r, θ, φ) стационарных состояний атома водорода определяются тремя квантовыми числами: 1) n - главное квантовое число, оно определяет энергию стационарных состояний; 2) l - азимутальное (или орбитальное) квантовое число, оно определяет момент импульса электрона (см. (8.4), (8.5)):
при заданном n квантовое число l может принимать следующие значения l = 0, 1,...(n - 1). 3) m l - магнитное квантовое число, оно определяет проекцию момента импульса на выбранное направление в пространстве, скажем ось z (см. (8.6), (8.7):
при заданном l магнитное квантовое число mе может принимать следующие значения:
3. Появление в шредингеровской теории атома водорода квантования момента импульса L и его проекции Lz объясняет некоторые особенности спектров излучения и поглощения атома водорода, которые не могли быть объяснены теорией Бора. 4. Особенности спектров атома водорода связаны с тем, что фотон обладает собственным моментом импульса. Поэтому, вследствие закона сохранения момента импульса, момент импульса атома в процессах излучения и поглощения фотонов меняется. С наибольшей интенсивностью идут такие переходы, в которых выполняется следующее правило отбора для квантового числа l (см. (8.9)):
5. Шредингеровская теория атома водорода позволяет учесть влияние на энергетические уровни (а следовательно и на спектры излучения и поглощения) магнитного поля (эффект Зеемана) и электрического поля (эффект Штарка). 6. Шредингеровская теория атома водорода позволяет объяснить тонкую и сверхтонкую структуры спектров атома водорода на основе представления о собственном (спиновом) моменте импульса электрона.
ЛЕКЦИЯ N 9
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1126; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.235.100 (0.008 с.) |



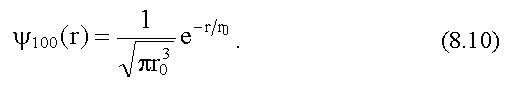
 - первый боровский радиус.
- первый боровский радиус.













