Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Различные формы записи уравнения Шредингера.Содержание книги Поиск на нашем сайте
Водородоподобных систем.
Полная система квантовых чисел. Принцип Паули. К-, L-, М- оболочки атома. Рентгеновский спектр. Закон Мозли. Энергетический спектр атомов и молекул. Заполнение электронных оболочек и периодическая система элементов.
Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом 2е (для атома водорода Z=1),
где r — расстояние между электроном и ядром. Состояние электрона в атоме водорода описывается волновой функцией y, удовлетворяющей стационарному уравнению Шредингера:
где т — масса электрона, Е — полная энергия электрона в атоме.
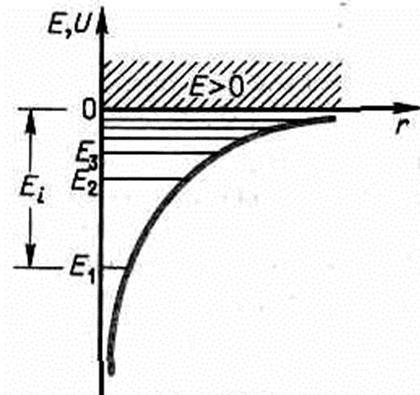
1. Энергия. Из уравнения Шредингера Решение уравнения Шредингера для атома водорода приводит к появлению дискретных энергетических уровней E 1, E 2, E 3 и т д. Самый нижний уровень Е1— основной, все остальные (En>E1 n=2, 3,...) — возбужденные.
Ei=-E1= те4/ (8h2e20) =13,55 эВ. 1. Квантовые числа. В квантовой механике доказывается, что уравнению Шредингера (223.2) удовлетворяют с yn m l(r, q, j), определяемые тремя квантовыми числами: главным n , орбитальным l. магнитным ml .
n=1,2,3,....
l= 0, 1,..., (n-1), т. е. всего n значений, и определяет момент импульса электрона в атоме. Из решения уравнений Шредингера следует также, что вектор Le момента импульса электрона может иметь лишь такие ориентации в пространстве, при которых его проекция
где ml — магнитное квантовое число, которое при заданном l может принимать значения ml=0, ±1, ±2,..., ±l, т. е. всего 2 l +1 значений.
Квантовые числа n и l характеризуют размер и форму электронного облака, а квантовое число ml характеризует ориентацию электронного облака в пространстве. В атомной физике, по аналогии со спектроскопией, состояние электрона, характеризующееся квантовыми числами l =0, называют s-состоянием (электрон в этом состоянии называют s-электроном), l =1 — р-состоянием, l =2 — d-состоянием,
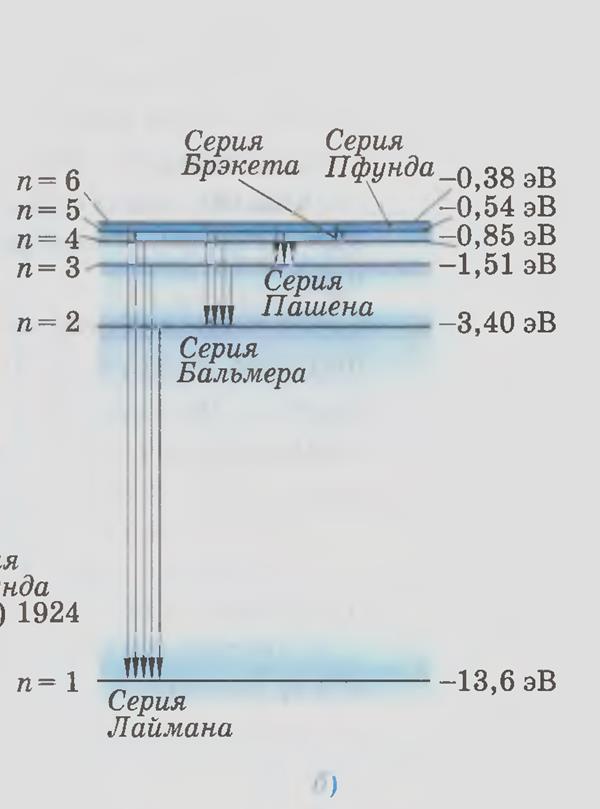
В квантовой механике вводятся правила отбора, ограничивающие число возможных переходов электронов в атоме, связанных с испусканием и поглощением света. 1) изменение орбитального квантового числа Dl удовлетворяет условию Dl=±1; 2) изменение магнитного квантового числа Dml удовлетворяет условию Dml=0, ±1. Учитывая число возможных состояний, соответствующих данному n, и правило отбора, рассмотрим спектральные линии атома водорода (рис. 304):
np®1s (n=2,3,...); Серии Бальмера. np®2s, ns®-2p, nd®2p (n=3, 4,...) И т. д.
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 363; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.176.191 (0.006 с.) |

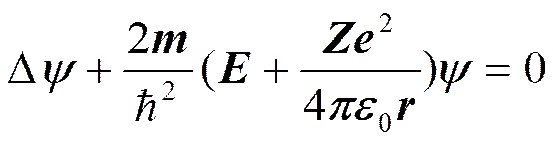




 ,
,


 на направление z внешнего магнитного поля принимает квантованные значения, кратные h
на направление z внешнего магнитного поля принимает квантованные значения, кратные h