
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция распределения Максвелла, Бозе-Эйнштейна, Ферми-Дирака.Содержание книги
Поиск на нашем сайте
1) Классическое распределение по скоростям (Максвелла): Справедливо для всех частиц:
dN = N·f(v)·dv dN – число частиц, попадающих в определенный интервал скоростей. N – число всех частиц. f(v) – функция распределения по скоростям dv – элементарный объем скоростей.
Рассмотрим функцию распределения по скоростям в сферической системе координат:
dV = 4pv2dv dN =N·f(v)·4pv2dv
f(v) = j(vx)·j(vy)·j(vz) ln f(v) = ln j(vx)+ln j(vy)+ln j(vz)
Величина А (амплитуда вероятности) находится из условия нормировки:
Аналогично находим j(vy) и j(vz):
тогда
v н.в. – наиболее вероятная
2) Функция распределения Бозе-Эйнштейна: Все частицы в квантовой статистике делятся на бозе-частицы и ферми-частицы (бозоны и фермионы). Бозоны – частицы с целым и нулевым спином, к таким частицам относятся фотоны и фононы. Фотоны – кванты электрического поля (или волн). Фононы – кванты звуковых волн. Фотоны – реальные частицы, фононы – квазичастицы. Для существования фононов необходима среда. В твердом теле как кристаллической решетке атомы колеблются около узлов кристаллической решетки. Эти колебания называются фононами, а для фотонов такой среды не нужно. Существует взаимодействие фотонов с фононами, это когда свет падает на металл (фотоэффект).
Закон распределения бозе-частиц (бозоны): Определяется как
< ni > - среднее число бозонов, имеющих энергию Еi. m - химический потенциал, химический потенциал – энергия, уносимая частицей из системы. 3) Ферми-частицы (фермионы) – представителями являются электроны. Электрон обладает спином 1/2·ħ (постоянная планка). Описание движения электронов в микромире (мир – размером 10-8 см–1А (ангстрем)) квантовой механикой, созданной Шредингером. В квантовой механике выполняется соотношение неопределенности Гейзенберга. В квантовой механике основным уравнением динамики является уравнение Шредингера. Для электронов, как и для других элементарных частиц квантовой механики, выполняется соотношение неопределенности Гейзенберга. Функция распределения Ферми-Дирака записывается в виде:
m - химический потенциал, в данном случае химический потенциал совпадает с энергией Ферми m = ЕF.
T = 00k
Распределение электронов по энергетическим уровням по два, прямопротивоположные спинам, на одном энергетическом уровне, называется принципом Паули.
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 403; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.31.64 (0.006 с.) |

 - функция распределения Максвелла.
- функция распределения Максвелла.







 - условие нормировки
- условие нормировки ;
; 


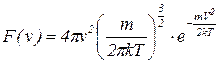
 Одномерная ось распространения:
Одномерная ось распространения:







