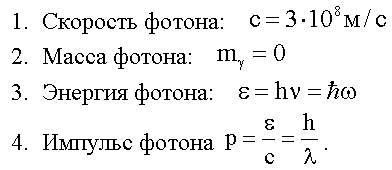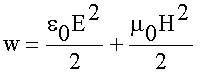Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерференция одиночных фотоновСодержание книги
Поиск на нашем сайте
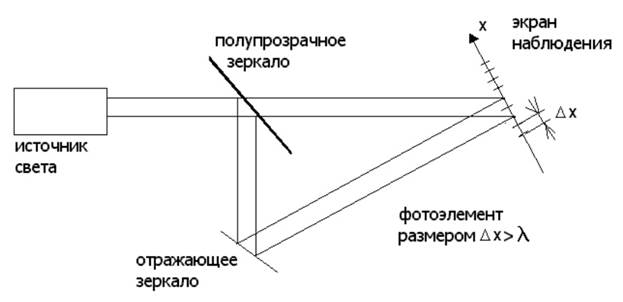
Дополним нашу установку по "расщеплению" фотонов еще одним элементом: зеркалом, отражающим второй пучок так, чтобы он встретился с первым. В месте встречи поставим экран наблюдения, вдоль которого расположим достаточно маленькие фотоэлементы, но их размер Δх должен быть больше, чем длина волны света λ.
Рис. 5.3 При большой интенсивности пучка I мы получим на экране наблюдения интерференционную картину от двух источников с чередованием максимумов и минимумов интенсивности. Ее можно наблюдать непосредственно, а можно зафиксировать с помощью нашей системы фотоэлементов, скажем, в памяти компьютера. Что произойдет, если интенсивность пучка опять сделать такой же малой, как и во второй части опыта по "расщеплению" фотонов, так, чтобы фотоны проходили нашу установку поодиночке? Получим мы в этом случае интерференционную картину или нет? Как мы знаем, интерференционная картина возникает от наложения двух (или больше) когерентных волн света (электромагнитных волн). Если фотон совершенно неделим, то при прохождении одиночных фотонов накладываться друг на друга нечему. И в этом случае интерференционная картина не должна сформироваться, сколько бы времени мы не накапливали информацию о срабатывании наших фотоэлементов в памяти компьютера (вспомните заключительную часть высказывания Милликена (см. лекцию N 3, § 2). Но опыт показывает, что с течением времени на экране наблюдения формируется интерференционная картина с тем же самым расположением максимумов и минимумов, как и при большой интенсивности света. Что же делится в нашей установке пополам и накладывается друг на друга? Делится электромагнитная волна, связанная с фотоном! В зависимости от разности хода две волны усиливают или ослабляют друг друга. Фотоны, как показывает опыт, чаще попадают в те места, где интенсивность волны больше. Это и приведет с течением времени к формированию одиночными фотонами интерференционной картины. § 4. Вероятностная интерпретация плотности энергии Результаты мысленных экспериментов, рассмотренных в (§2) и (§3), позволяют сформулировать некоторые выводы. 1. Распространение фотонов в пространстве в некотором смысле правильно описывается уравнениями Максвелла для электромагнитной волны. Электромагнитная волна, падающая на полупрозрачное зеркало, действительно "расщепляется" на две волны, которые могут интерферировать друг с другом. 2. Величины 3. Правильная интерпретация величин, пропорциональных E2 и Н2, состоит в том, что они определяют вероятность обнаружения фотона в некоторой области пространства. Таким образом, энергию переносит фотон, а электромагнитная волна дает только вероятность обнаружения этого фотона. Плотность энергии w одиночного фотона равна произведению энергии фотона на вероятность его нахождения в данной области пространства. При очень большом числе фотонов (больших интенсивностях света) величина w дает среднюю плотность энергии, создаваемую этими фотонами. Итоги лекции N 5 1. Корпускулярно-волновой дуализм микрообъектов заключается в том, что всем им (фотонам, электронам, протонам, нейтронам и т.д.) присущи одновременно и корпускулярные и волновые свойства. 2. Фотон - это элементарная частицы, квант электромагнитного излучения. Он обладает следующими свойствами:
3. Распространение фотонов в пространстве в некотором смысле правильно описывается уравнениями Максвелла для электромагнитных волн, при этом величины плотности энергии электромагнитной волны в вакууме:
и интенсивности I ~ E2 - для одиночных фотонов определяют вероятность обнаружить фотон в некоторой области пространства.
ЛЕКЦИЯ N 6
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1838; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.2.239 (0.009 с.) |

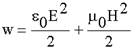 и I ~ E2 в случае малой интенсивности волны (малых значений напряженности электрического поля E и индукции магнитного поля
и I ~ E2 в случае малой интенсивности волны (малых значений напряженности электрического поля E и индукции магнитного поля 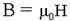 ) не могут быть истолкованы как плотность энергии и плотность потока энергии (интенсивность света). Величина w (также как и I) может быть сделана сколь угодно малой, а энергия, передаваемая фотоном фотоэлементу, всегда конечна и равна!
) не могут быть истолкованы как плотность энергии и плотность потока энергии (интенсивность света). Величина w (также как и I) может быть сделана сколь угодно малой, а энергия, передаваемая фотоном фотоэлементу, всегда конечна и равна!