
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Потенциальная энергия во внешнем поле.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Если частица находится в поле консервативных сил, то каждой точке поля можно сопоставить значение некоторой функции координат так, что работа сил поля при переходе между некоторыми двумя точками будет равна разности значений U(x, y, z) в этих точках поля. Эту функцию по определению и называют потенциальной энергией частицы во внешнем поле сил. Формально определение такой функции можно сделать следующим образом. Припишем некоторой исходной точке О произвольное значение Uо. Любой другой точке Р припишем значение
Соответственно разность значений U в точке 1 и точке 2:
Учитывая, что работа при перемещении из точки 2 в точку О
Сумма, стоящая в правой части соотношения (3.20) есть работа, совершаемая силами поля при перемещении частицы из 1 и 2 по траектории, проходящей через точку О. Но, поскольку силы консервативные, эта работа не зависит от формы пути и равна просто
Поэтому рассмотренная нами функция U(Р) соответствует определению потенциальной энергией частицы во внешнем поле сил. Как следует из соотношения (3.21), работа консервативных сил
т.е. равна убыли потенциальной энергии. Отметим важную особенность определения потенциальной энергии в виде функции U(Р): потенциальная энергия определена нами с точностью до произвольной постоянной Uо, т.е. до значения приписанного некоторой произвольной исходной точке О. На первый взгляд может показаться, что такое определение оказывается странным, поскольку абсолютное значение потенциальной энергии в данной точке оказывается произвольным! В действительности это обстоятельство оказывается очень удобным, поскольку обеспечивает возможность выбора начало отсчета энергии желательным образом, так, как это необходимо при решении конкретной задачи. В то же время во все физические соотношения входит либо разность значений U, либо её производная, и потому константа Uо не усложняет их. Поле консервативных сил является частным случаем потенциального поля. Потенциальным называют поле, которое можно описать с помощью некоторой функции П (x, y, z, t) градиент которой равен силе, действующей в каждой точке поля:
Функция ПОЛНАЯ МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Как мы установили ранее (см. соотношение (3.10)), работа результирующей силы, действующей на частицу, идет на приращение ее кинетической энергии. Если на частицу действуют только консервативные силы, то их работа равна по формуле (3.22) равна убыли потенциальной энергии (
Перегруппируем члены в соотношении (3.24) по индексам следующим образом:
Формула (3.25) означает, что в отсутствие неконсервативных сил величина
не изменяется при движении частицы, а значит, является интегралом движения. Эту величину называют полной механической энергией частицы. Если рассматриваемая система состоит из N невзаимодействующих частиц, находящихся в поле консервативных сил, то полная энергия системы
Тогда
Однако полная энергия сохраняется не всегда. Рассмотрим ситуацию, когда на частицу кроме консервативных
Поскольку суммарная работа всех сил идет на приращение кинетической энергии, то можно записать
Группируя в (3.30) слагаемые, получаем:
А это означает, что работа неконсервативных сил равна приращению полной механической энергии частицы. Типичными неконсервативными являются силы трения и сопротивления среды. Работа этих сил, как правило, отрицательна, поскольку они направлены противоположно перемещению. Поэтому действие этих сил обычно приводит к убыли (ΔЕ < 0) полной энергии за счет её перехода во внутреннюю энергию тел. Этот процесс называется диссипацией энергии, а соответственно силы, обеспечивающие ее, – диссипативными.
|
||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1145; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 (3.17)
(3.17) где Аро - работа консервативных сил при перемещении частицы из точки Р в О. Значения определенной таким образом функции U(Р) в некоторых точках 1 и 2 будут равны:
где Аро - работа консервативных сил при перемещении частицы из точки Р в О. Значения определенной таким образом функции U(Р) в некоторых точках 1 и 2 будут равны: и
и 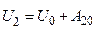 (3.18)
(3.18) (3.19)
(3.19) (все перемещения заменяются на обратные), получаем
(все перемещения заменяются на обратные), получаем (3.20)
(3.20) - работе при перемещении из точки 1 в 2, по произвольной траектории:
- работе при перемещении из точки 1 в 2, по произвольной траектории: (3.21)
(3.21) (3.22)
(3.22) (3.23)
(3.23) называется потенциальной, и, если она не зависит от времени, то силы поля являются консервативными, а сама потенциальная функция равна взятой с обратным знаком потенциальной энергии частицы: П (x, y, z) = -U (x, y, z).
называется потенциальной, и, если она не зависит от времени, то силы поля являются консервативными, а сама потенциальная функция равна взятой с обратным знаком потенциальной энергии частицы: П (x, y, z) = -U (x, y, z). ) и идет на приращение кинетической энергии частицы:
) и идет на приращение кинетической энергии частицы: . (3.24)
. (3.24)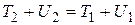 . (3.25)
. (3.25)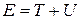 (3.26)
(3.26) также является интегралом движения. Действительно, для каждой частицы справедливо соотношение (3.23), поэтому
также является интегралом движения. Действительно, для каждой частицы справедливо соотношение (3.23), поэтому (3.27)
(3.27) (3.28)
(3.28) действует не консервативная сила
действует не консервативная сила  (3.29)
(3.29)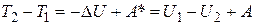 . (3.30)
. (3.30) . (3.31)
. (3.31)


