
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинетическая энергия и работа при вращательном движении телаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Рассмотрим твердое тело, вращающееся с угловой скоростью
Учитывая, что линейная скорость
Кинетическая энергия тела, обусловленная его вращением (!), складывается из кинетических энергий отдельных частиц:
где Работа, совершаемая всеми приложенными к телу силами, идет на увеличение его кинетической энергии. Поэтому
где Таким образом,
Если внимательно сравнить формулы для вращательного и поступательного движений, то легко установить аналогию величин и формул:
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
Мы рассматривали два основных вида движения: поступательное и вращательное. При поступательном движении скорости и ускорения всех точек тела одинаковы, поэтому для описания движения всего тела достаточно определить движение одной точки тела. Для описания вращательного движения необходимо задать положение в пространстве оси вращения и угловую скорость в каждый момент времени. Можно доказать, что произвольное движение тела можно представить в виде наложения двух основных видов движения. Наиболее просто это можно показывать для плоского движения, т.е. такого движения, при котором точки тела перемещаются в параллельных плоскостях.
Заданное плоское перемещение можно представить также как промежуточное поступательное перемещение (рисунок 4.6 - с) c последующим вращением относительно промежуточной оси «О'» на тот же угол φ. Наконец требуемое перемещение можно представить как чисто вращательное движение относительно оси «О'' » -рисунок 4.6 - d. Примечательно, что для любой оси вращения поворот происходит на один и тот же угол φ. Рассуждая аналогично, произвольное элементарное перемещение
Разделив это соотношение на
где
Обозначив скорость поступательного движения центра масс в выбранной системе отсчета
При качении цилиндра по плоскости (рисунок 4.7) без проскальзывания мгновенной осью вращения является линия касания цилиндра и плоскости. Относительно этой оси скорость центра масс
При качении цилиндра с проскальзыванием так, что  (ведущее колесо автомобиля проскальзывает при разгоне), мгновенная ось вращения оказывается в пределах тела (рисунок 4.8). Она, очевидно, совпадет с осью, проходящей через (ведущее колесо автомобиля проскальзывает при разгоне), мгновенная ось вращения оказывается в пределах тела (рисунок 4.8). Она, очевидно, совпадет с осью, проходящей через
центр масс, если будет наблюдаться полное проскальзывание, т.е скорость автомобиля будет равна нулю. При качении цилиндра с проскальзыванием (рисунок 4.9) так, что
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1111; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 вокруг некоторой оси. Считая тело состоящим из жестко связанных частиц, для кинетической энергия
вокруг некоторой оси. Считая тело состоящим из жестко связанных частиц, для кинетической энергия 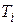 некоторой частицы массой
некоторой частицы массой  , движущейся, вследствие вращения тела, с линейной скоростью
, движущейся, вследствие вращения тела, с линейной скоростью  можем утверждать:
можем утверждать: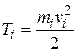 (4.20)
(4.20) -той частицы
-той частицы 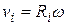 , для кинетической энергии частицы находим:
, для кинетической энергии частицы находим: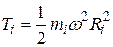 (4.21)
(4.21) (4.21)
(4.21)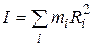 - момент инерции тела.
- момент инерции тела.

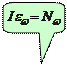
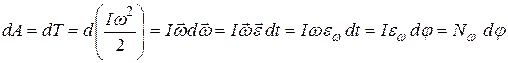 , (4.21)
, (4.21)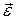 есть угловое ускорение тела.
есть угловое ускорение тела. (4.22)
(4.22)
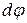




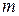

 (вокруг оси симметрии)
(вокруг оси симметрии)
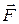




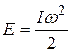
 Действительно, плоское перемещение тела из положения «I» в «II» (рисунок 4.8 - а _) можно представить в виде двух последовательных перемещений: сначала поступательного, до перемещения центра масс в заданное положение, а потом - поворота вокруг оси «О», проходящей через его центр масс, на необходимый угол φ (рисунок 4.6 - b).
Действительно, плоское перемещение тела из положения «I» в «II» (рисунок 4.8 - а _) можно представить в виде двух последовательных перемещений: сначала поступательного, до перемещения центра масс в заданное положение, а потом - поворота вокруг оси «О», проходящей через его центр масс, на необходимый угол φ (рисунок 4.6 - b). точки тела, заданной радиус-вектором
точки тела, заданной радиус-вектором 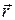 за время
за время  , можно представить в виде суммы перемещения
, можно представить в виде суммы перемещения 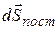 , обусловленного поступательным движением, и перемещения
, обусловленного поступательным движением, и перемещения  , обусловленного вращением:
, обусловленного вращением: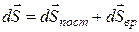 . (4.23)
. (4.23) (4.24)
(4.24) - одинаковая для всех точек тела скорость, обусловленная поступательным перемещением в выбранной системе отсчета,
- одинаковая для всех точек тела скорость, обусловленная поступательным перемещением в выбранной системе отсчета, - скорость, обусловленная вращением, зависящая от положения точки, т.е. от ее радиус-вектора
- скорость, обусловленная вращением, зависящая от положения точки, т.е. от ее радиус-вектора 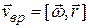 .
. , (
, (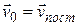 ) можем утверждать, что скорость точки тела при сложном движении определяется соотношением:
) можем утверждать, что скорость точки тела при сложном движении определяется соотношением: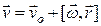 (4.25)
(4.25)
 Очевидно, что всегда можно указать совокупность радиус-векторов, задающих положение точек для которых выполняется условие
Очевидно, что всегда можно указать совокупность радиус-векторов, задающих положение точек для которых выполняется условие  , т.е. скорость поступательного движения центра масс относительно неподвижной системы отсчета оказывается равной нулю. Эти радиус векторы определяют положение прямой, относительно которой движение тела можно считать чисто вращательным. Такую прямую называют мгновенной осью вращения. Она может находиться как в пределах движущегося тела, так и вне него.
, т.е. скорость поступательного движения центра масс относительно неподвижной системы отсчета оказывается равной нулю. Эти радиус векторы определяют положение прямой, относительно которой движение тела можно считать чисто вращательным. Такую прямую называют мгновенной осью вращения. Она может находиться как в пределах движущегося тела, так и вне него.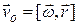 .
.

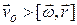 (колесо автомобиля проскальзывает, но не заблокировано, при торможении), мгновенная ось вращения оказывается вне пределов тела. При полной блокировке колеса, т.е. при поступательном движении цилиндра без вращения, ось вращения оказывается на бесконечности. Соответственно поступательное движение можно рассматривать как вращательное относительно мгновенной оси, находящейся на бесконечности.
(колесо автомобиля проскальзывает, но не заблокировано, при торможении), мгновенная ось вращения оказывается вне пределов тела. При полной блокировке колеса, т.е. при поступательном движении цилиндра без вращения, ось вращения оказывается на бесконечности. Соответственно поступательное движение можно рассматривать как вращательное относительно мгновенной оси, находящейся на бесконечности.


