
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинетическая энергия при плоском движенииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим, как вычислить кинетическую энергию тела, если оно одновременно участвует в поступательном и вращательном движении – например, качение колеса по плоскости. Как мы знаем, при плоском движении тела скорость некоторой точки тела определяется формулой
где
Учтем, что модуль Тогда из (4.27) получим:
А для кинетической энергии всего тела
Теперь учтем, что
Тогда
Если в качестве «0» взять центр масс, то
Таким образом, если рассматривать вращение тела относительно оси, проходящей через центр масс, то его кинетическая энергия распадается на два слагаемых. Одно из них описывает кинетическую энергию, обусловленную поступательным движением, другое – вращательным. ГИРОСКОПЫ. Гироскопом называют массивное симметричное тело, вращающееся с БОЛЬШОЙ УГЛОВОЙ СКОРОСТЬЮ вокруг оси симметрии.
При попытках повернуть ось гироскопа возникает гироскопический эффект: под действием сил, стремящихся повернуть ось гироскопа вокруг оси
Если момент Гироскопический эффект лежит в основе действия гирокомпаса, который представляет собой гироскоп, точки опоры которого закреплены так, что гироскоп может поворачиваться вокруг вертикальной оси. На раскрученный гироскоп через точки опоры действует момент сил, вовлекающий его в суточное вращение Земли. При длительном воздействии этого момента, ось гироскопа устанавливается параллельно оси вращения Земли, т.е. в меридиональной плоскости, и позволяет определить направление на географический (!) полюс. Если гироскоп находится в поле силы тяжести и его ось составляет с вертикалью угол
Под действием момента сил
Такое движение называется прецессией. Соотношение (4.33) дает угловую скорость прецессии. Очевидно, что чем больше момент импульса гироскопа
ЛЕКЦИЯ 5. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ. ВВОДНЫЕ ЗАМЕЧАНИЯ. Колебаниями будем называть процессы, отличающиеся той или иной степенью повторяемости. В зависимости от физической природы повторяющегося процесса различают механические колебания, электрические и т.п. В зависимости от характера воздействия на колеблющуюся систему различают свободные (собственные), вынужденные, автоколебания и параметрические колебания. Свободными называют колебания, которые возникают в системе, предоставленной самой себе, после того, как она каким либо образом была выведена из положения равновесия. Вынужденными называют колебания, совершаемые системой под действием внешней периодически изменяющейся силы. При автоколебаниях воздействием внешних сил управляет сама система. Например, маятник часов. Параметрическиминазывают колебания, возникающие за счет того, что внешнее воздействие изменяет какой-либо параметр системы. Простейшими колебаниями являются гармонические колебания, при которых колеблющаяся величина изменяется по закону синуса или косинуса. Таким колебаниям уделяют особое внимание, так как: 1 очень часто колебания реальных систем близки к гармоническим и, кроме того, 2 можно доказать, что периодические процессы произвольной формы могут быть представлены как наложение гармонических колебаний.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 707; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.106.176 (0.011 с.) |

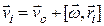 (4.26)
(4.26) - скорость поступательного движения точки «0», принятой за начало отсчета для
- скорость поступательного движения точки «0», принятой за начало отсчета для  ,
, по отношению к точке «0». Тогда кинетическая энергия i -той частицы
по отношению к точке «0». Тогда кинетическая энергия i -той частицы (4.27)
(4.27) ,
,  - расстояние i -той точки до оси вращения и, соответственно
- расстояние i -той точки до оси вращения и, соответственно 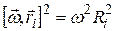 . Воспользовавшись циклической перестановкой сомножителей в смешенном произведении, получим
. Воспользовавшись циклической перестановкой сомножителей в смешенном произведении, получим 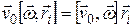 .
. (4.28)
(4.28)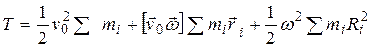 (4.29)
(4.29)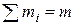 ,
, 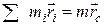 , а
, а 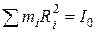 .
. (4.30)
(4.30)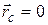 , и
, и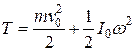 (4.31)
(4.31)
 В этом случае момент импульса гироскопа
В этом случае момент импульса гироскопа 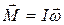 . Если мы будем поворачивать ось гироскопа с некоторой
. Если мы будем поворачивать ось гироскопа с некоторой  в пространстве, то
в пространстве, то 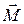 , вообще говоря, не совпадает с осью гироскопа. Однако обычно
, вообще говоря, не совпадает с осью гироскопа. Однако обычно  и можно считать, что
и можно считать, что  декартовой системы координат, гироскоп поворачивается вокруг оси
декартовой системы координат, гироскоп поворачивается вокруг оси  .
. Такое поведение объясняется законами динамики вращательного движения. Действительно момент пары сил,
Такое поведение объясняется законами динамики вращательного движения. Действительно момент пары сил, 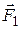 ,
, 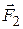 направленных вдоль
направленных вдоль  получает приращение
получает приращение 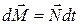 направленное вдоль
направленное вдоль  . Следовательно, ось гироскопа приблизится к направлению –
. Следовательно, ось гироскопа приблизится к направлению –  , то к гироскопу оказывается приложенным момент сил
, то к гироскопу оказывается приложенным момент сил 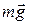 , которая приложена к центру масс гироскопа и реакцией опоры
, которая приложена к центру масс гироскопа и реакцией опоры 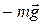 , действующей в точке опоры
, действующей в точке опоры 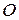 . Раскрученный гироскоп не падает, как «юла»! Поэтому эти силы равны и противоположны по направлению. Момент сил
. Раскрученный гироскоп не падает, как «юла»! Поэтому эти силы равны и противоположны по направлению. Момент сил 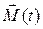 гироскопа в некоторый исходный момент времени. Если расстояние от точки опоры до центра масс гироскопа равно
гироскопа в некоторый исходный момент времени. Если расстояние от точки опоры до центра масс гироскопа равно  , то модуль этого момента сил
, то модуль этого момента сил
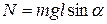 (4.32)
(4.32) , а ось гироскопа за
, а ось гироскопа за  повернется на угол
повернется на угол 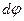 . Следовательно, ось гироскопа будет совершать вращательное движение вокруг вертикали с угловой скоростью:
. Следовательно, ось гироскопа будет совершать вращательное движение вокруг вертикали с угловой скоростью: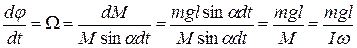 (4.33)
(4.33)


