
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон сохранения количества движенияСтр 1 из 3Следующая ⇒
Закон сохранения количества движения Даны m1, m2, …, mn V1, V2,…, Vn F’ – внутренняя сила F – внешняя сила
Просуммируем данное выражение по всем точкам системы:
Поэтому Если система замкнута, то F=0 => Таким образом, кол-во движения замкнутой системы есть величина постоянная Центр масс. Закон движения центра масс Центр масс системы мат. точек называется точка С с радиус-вектором rc= Vc= P=mVc
Таким образом, центр масс системы мат. точек движется как мат. точка, масса которой равна массе всей системы и на которую действует сила, равная векторной сумме всех внешних силб действующих на систему Закон движения переменной массы. Формула Циолковского Предположим, что в начальный момент ракета имела массу m и скорость V, а по истечению времени dt часть топлива сгорела, тогда (m-dm); V+dV. Найдем изменение импульса системы:
dP=mdV-Udm
Если F=0,
mdV=-Udm
VMAX=U*ln(m/m-mт) – формула Циолковского Работа силы. Мощность В качестве единой количественной меры различных форм движения материи вводится скалярная величина называется энергией Изменение мех. энергии происходит в результате действия силы и для количественного описания процесса изменения энергии вводится понятие работы силы. бА – элементарная работа. Совершаемая силой F за dt бА=Fdr=FVdt бА=Fdr*cosα=Fτdr= FτdS – скалярная форма F=Fxi+Fyj+Fzk dr=dx*i+dy*j+dz*k бА= Fxdx+Fydy+Fzdz Сила F – потенциальная, если работа этой силы зависит от положения начальной и конечной точек движения Таким образом, работа потенциальной силы по замкнутой траектории равна нулю. Иначе говоря, Мощность
10. Преобразование Галилея. Механический принцип относительности Рассмотрим две системы отсчета: К – инерциальная, К' – движется относительно первой равномерно и прямолинейно со скоростью U.
r=r’+rOO’=r’+Ut
V=V’+U – правило сложения скоростей в классической механике
Если а=0, то а’=0, таким образом, С.О. K’ движется относительно инерциальной С.О. и так же будет инерциальной. Во всех инерциальных С.О. законы классической механики имеют одинаковую форму.
Механическая энергия. Закон сохранения механической энергии. В физике механическая энергия описывает сумму потенциальной и кинетической энергий, имеющихся в компонентах механической системы. Механическая энергия — это энергия, связанная с движением объекта или его положением, имеющая способность совершать механическую работу. Wk + Wp = const О. Если действующие на мех. систему силы стационарны и потенциальны, а внутренние силы потенциальны, то такая система наз-ся консервативной и сумма энергии потенциальной и стационарной есть величина постоянная. Виды механической энергии. В механике различают два вида энергии: кинетическую и потенциальную. Кинетической энергией называют механическую энергию всякого свободно движущегося тела и измеряют ее той работой, которую могло бы совершить тело при его торможении до полной остановки. Ek Потенциальная энергия – это механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними. Ep = mgh Момент инерции цилиндра относительно его оси. 1) тонкостенный цилиндр: Jc = mR2 2) cплошной цилиндр: Jc = Момент инерции стержня относительно перпендикулярной оси. Момент инерции стержня относительно оси, проходящей через центр масс,
а относительно оси ВВ,
Кинетическая энергия вращения. Wвр =
Wk = Ур-е Клайперона-Менделеева P1V1=P1’V2; P1’/T1=P2/T2 P1V1/T1=P2V2/T2 -ур-е Клайперона P*Vm/T=R -универсальная газовая постоянная для 1 моля V=m/M=Y(ню)=N/Na PV=m/M*R*T -ур-е Клайперона-Менделеева. R=K*Na,где K-Постоянная Больцмана; n=N/V => P=nKT Распределение молекул идеального газа по кинетическим энергиям
Барометрическая формула Барометрическая формула определяет зависимость давления газа с высотой h с учетом силы тяготения.
Справедливо для любого потенциального поля.
9 вопрос. Средняя длина пробега молекул
Расстояние l, кот молекула пролетает между 2-мя ближайщими столкновениями с другими молекулами наз-ся молек. свободного пробега. Расстояние, проходимые молек. за одну сек.в среднем равно<v>при этом она может испытать <z> <l>=<v>/<z> При своем движ. молек. может столкнуться только с теми, центры кот.лежат внутри ломаного цилиндра, высота кот. Равно ср.ариф. скорости и радиусом основания равным диаметру. <z>=n<v>pd^2 <l>=<v>/(n<V>pd^2)=1/(pnd^2) Длина свободного пробега будет зависеть от относ.скорости молек.,т.к другие молек.тоже движ. Vотн=V1-V2 Vотн^2=(V1-V2)^2=V1^2-2V1V2+V2^2 Vотн^2=V1^2+V2^2-2V1V2 <Vотн^2>=<V1^2>+<V2^2> - 2<V1V2> События, заключающиеся в том, что 1 молек. имеет V, а 2-V являются статистически независимыми <V1V2>=<V1><V2> Ср.ариф. скорость равно 0 Vотн=sqrt<Vотн>=sqrt(2)Vср.кв Ср кв.скорость ~ср.ариф <Vотн>=sqrt(2)<V> <l>=1/sqrt(2pd^2n) l/l=n/n2 10 вопрос. Внутр.энергия идеального газа В модели идеального газа не учитывается взаимодействие молекул между собой и над внут.энергией идеального газа понимается совокупность энергии всех газов. Внутр.энергия U является однозначной функцией состоянии системы, поэтому при возвращ. сис. в исход. Изменение будет равно 0. DU=U2-U1 Молекулы газа имеют различные степени свободы iпост=3 iвр=2 I=mr=0 W=(Iv^2)/2=0 Согласно закону Больцмана на каждую степень свободы вращ и пост движ приходится энергия 1/(2kT) i=iпост+iвр+2iкол U=1/2ikT=UAUO=m/(m)i/2RT внутр.энергия газа зависит от числа степени свободы и температуры газа 11 вопрос. 1-е начало термодинамики. Закон сохранения энергии для тепловых процессов. Внутр. Энергия газа может изменяться 2-мя способами: 1)Путем сообщения сис некот кол-ва теплоты Q 2)-/- работы над сис внешних сил DU1-2=А’1-2+Q1-2 Q1-2=DU1-2+ А1-2 dQ=dU+dA Каждая из величин может иметь тот или иной знак dA=pdV, dV>0 ->dA>0 dV<0->dA<0 dU=0 ->dA=dQ А1-2= Q1-2 Совершаемая сис рабоа может быть больше, чем кол-во теплоты сообщенной системе.
12 вопрос. Теплоемкость идеального газа Теплоемкостью тела наз-ся величина=отнош кол-ва теплоты dQ к изм температуры dT CT=dQ/dT C=mс Значение теплоемкости зависит от вида процесса перехода сис от одного состояния к другому dQ=dUm+dA CdT=dUm+pdVm V=const Cv=(dQ/dT)v= dUm/dT=d(i/2RT)/dT=i/2R P=const Cp=(dQ/dT)p= dUm/dT+p dVm/dT= Cv+R Cp= Cv+R -ур-е Майера Молярная теплоемкость зависит от числа сепеней свободы и не зависит от температуры. Однако она справедлива толька для одноатомного моль. График-ступенчатый, обучловлен энергией вращ.движ. и энергией колеб.движ.Если энергия теплового движ не достаточна, для возбуждения колебаний, то они не вносят вклада во внутр.энергию и теплоемкость. Колеб степени свободы замораживаются. 13 вопрос. Применение 1-го начала термодинамики к изопроцессам P=const dQ=dU+dA dQ=Cpm/mRdT dU=Cvm/mRdT dA=pdV A= V=const dQ=dU dU= Cvm/mdT=dQ dA=0 T=const dQ=dA=pdV A= 14. Адиабатный процесс. Уравнение Пуассона для адиабатного процесса. Уравнение адиабаты (уравнение Пуассона). Адиабатическим называется процесс, происходящий без теплообмена с окружающей средой. Следовательно, для него характерно наличие хорошей изоляции ТС от внешней среды или высокая скорость термодинамического процесса, при которой теплообмен незначителен. Поскольку обратимые процессы, в отличии от адиабатных, являются бесконечно медленными, то о равновесности последних можно говорить только применительно к определенным областям ТС.
Поскольку для адиабатического процесса Q = 0, то A = - dU. Следовательно, p·dV = - (m/)·Cv·dT. (1) Следовательно, работа газа при адиабатическом расширении равна A1-2 = (m/)·Cv·(T1 - T2). (2) Выразив величину P из уравнения Менделеева-Клапейрона и подставив ее в (1), после соответствующих преобразований получим уравнение адиабаты: T·V-1 = const или Уравнение (3) называется также уравнением Пуассона. На диаграмме P-V адиабата испытывает более резкое падание, чем изотерма, т.е. в любой точке кривой модуль производной от давления по объему для нее больше. Действительно, из уравнения адиабаты можно показать, что dp/dV = - ·p/V > p/V.
15. Круговые процессы (термодинамические циклы) Круговым процессом или циклом называется такой процесс, в результате которого термодинамическое тепло возвращается в исходное состояние. В p-V диаграмме круговые процессы изображаются в виде замкнутых кривых. Это связано с тем, что в любой диаграмме два тождественных состояний (в данном случае начало и конец кругового процесса) изображаются одной и той же точкой на плоскости.
Круговые процессы лежат в основе всех тепловых машин, двигателей внутреннего сгорания, паровых и газовых турбин, холодильных машин и т. д. Рассмотрим произвольный круговой процесс а) расширения С1аС2 и б) сжатия С2вС1 При расширении газ совершает положительную работу А1 измеряемый площадью
Она измеряется заштрихованной площадью на рис. Такой цикл называют прямым. Определение обратного процесса. а) Если бы круговой процесс (цикл) протекал в обратном направлении (против часовой стрелки), то суммарная работа, совершаемая газом за цикл, оказалась бы отрицательной. Численно она измерялась бы площадью той же заштрихованной области. Такой цикл называется обратным. Мы уже говорили, что внутренняя энергия тела зависит только от его состояния. Тогда изменение внутренней энергии газа в результате ругового процесса равна нулю. Следовательно по I началу термодинамики
где Q общее количество теплоты сообщаемое газу в круговом процессе А – работа газа в этом процессе. В прямом цикле А>0 и Q>0, т. е. газ совершает работу за счет сообщенной ему теплоты. В тепловом двигателе рабочее тело совершает прямой цикл, а в холодильной машине – обратный.
Как мы видим в рассматриваемом круговом процессе не все количество теплоты Q1, переданное веществу во время прямого цикла, оказывается превращенной в работу, часть тепла отдается окружающим телам. Поскольку передача тепла происходит само собой только от более горячего тала к более холодному, то должны существовать: более горячее тело (нагреватель), передающее веществу количество теплоты Q1 и более холодное тело, которому вещество отдает количество теплоты Q2 (холодильник). При получении работы за счет переданного количества тепла выполняется закон сохранения энергии: разность Q1 – Q2 равна полученной работе. С практической точки зрения представляет интерес, какая часть взятого от нагревателя тепла превращена в работу. Поэтому вводится понятие К. П. Д.
К. П. Д. определяется для каждого конкретного цикла. Разберем круговой процесс, введенный впервые в рассмотрение основателем термодинамики французским инженером Сади Карно и получивший название цикла Карно.
16) Второе начало термодинамики Для описания термодинамических процессов первого начала термодинамики недостаточно, так как этот закон, являясь по сути законом сохранения энергии в тепловых процессах, не позволяет определить направление протекаемых процессов в природе. Совершенная работа A=Q1-Q2 N=A/Q=(Q1-Q2)/Q1; n=1, если Q2=0 Цикл Карно показал, что невозможен процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, эквивалентной её работе. 2 начало термодинамики - формулировка, данная Кельвином и Планком
В обратном цикле рабочее тело отнимает теплоту от менее нагретого тела и передает более нагретому. Q2-Q1=A; A=-A’; Q1=Q2+A’ Теплота не может сама собой переходить от менее нагретого к более нагретому телу. Передаваемая более нагретому телу Q1 больше теплоты, отнимает от менее нагретого величину работы, совершаемой силой над системой(формулировка Клаузиуса) Для любого процесса изменяется внутр энергия=0, то есть A=Q
Обратный цикл Карно. Теплота Q1<0, Q2>0.
Работа, совершаемая рабочим телом за цикл будет отрицательная A=Q2-|Q1| Ɛ =
Ƞ =
19) Энтропия.
Для цикла Карно, алгебраическая сумма приведенного количества теплоты остается неизменным. Из равенства интеграла 0, взятого по замкнутому контуру следует, что подынтегральное выражение Функция состояния, дифференциалом которой является Для обратных процессов изменение энтропии = 0, это вытекает из равенства В термодинамике доказывается, что для системы совершающего необратимый процесс
Энтропия замкнутой системы может либо возрастать в случае необратимых процессов, либо оставаться неизменной в случае обратимых процессов. // (Неравенство Клаузиуса) В природе возможны лишь такие процессы, которые ведут к увеличению энтропии системы.
Закон сохранения количества движения Даны m1, m2, …, mn V1, V2,…, Vn F’ – внутренняя сила F – внешняя сила
Просуммируем данное выражение по всем точкам системы:
Поэтому Если система замкнута, то F=0 => Таким образом, кол-во движения замкнутой системы есть величина постоянная
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 241; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.20 (0.09 с.) |


 т.к в ней присутствуют парные силы, компенсирующие друг другом
т.к в ней присутствуют парные силы, компенсирующие друг другом
 =>
=> 


 =>
=>  – закон движения центра масс
– закон движения центра масс , где V-V’=U – скорость истечения газов по отношению к самой движущ. Ракете
, где V-V’=U – скорость истечения газов по отношению к самой движущ. Ракете
 , где
, где  =FR – реактивная сила
=FR – реактивная сила
 – скалярный вариант
– скалярный вариант решая диф. уравнение, получим
решая диф. уравнение, получим


 =>
=>




 =
=  =
= 
 i =wri
i =wri
 ,
,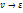 :
:  ,
,  ;
; 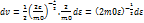
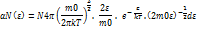
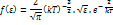

 )
) ,
,  ;
;
 ,
, ,
,  ,
,  ,
,  =>
=> 
 A, En=mngh =>
A, En=mngh => 
 dU=0
dU=0 m/mRd(T2-T1)
m/mRd(T2-T1) =m/mRT
=m/mRT  = m/mRT ln V2/V1= m/mRT P1/P2
= m/mRT ln V2/V1= m/mRT P1/P2
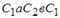 , совершаемый идеальным газом. Его можно разбить на два процесса
, совершаемый идеальным газом. Его можно разбить на два процесса . Для сжатия газа внешние силы совершают работу – А2, измеряемой площадью
. Для сжатия газа внешние силы совершают работу – А2, измеряемой площадью  Поэтому за цикл газ совершает положительную работу
Поэтому за цикл газ совершает положительную работу




 (стрелочки наоборот)
(стрелочки наоборот)
 - Холодильный коэффициент равен количеству отводимой теплоты от менее нагретого тела и работе, совершаемой внешними силами.
- Холодильный коэффициент равен количеству отводимой теплоты от менее нагретого тела и работе, совершаемой внешними силами. =
=  ;
;  |Q1|- Q2; Ɛ=
|Q1|- Q2; Ɛ=  ;
; =
=  ;
;  =
=  ;
;  =
=  ;
; +
+ 
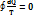
 является полным дифференциалом некоторой функции состояния системы.
является полным дифференциалом некоторой функции состояния системы. называется энтропией системы.
называется энтропией системы. .
. только возрастает.
только возрастает.


